
- •§ 4. Интегрирование тригонометрических функций
- •1473. Найти интеграл
- •1474. Найти интеграл
- •1475. Найти интеграл .
- •1476. Найти интеграл
- •6. Интегралы вида .
- •1487. Найти интеграл .
- •1488. Найти интеграл .
- •1506. Найти интеграл
- •1507. Найти интеграл
- •1508. Найти интеграл
- •§ 5. Интегрирование разных функций
- •Глава X определенный интеграл
- •§ 1. Вычисление определенного интеграла
- •§ 2. Несобственные интегралы
- •§ 3. Вычисление площади плоской фигуры
- •§ 4. Вычисление длины дуги плоской кривой
- •§ 5. Вычисление объема тела
- •1. Вычисление объема тела по известным площадям поперечных сечений.
- •§ 6. Вычисление площади поверхности вращения
§ 2. Несобственные интегралы
1. Основные понятия. Несобственными интегралами называются: 1) интегралы с бесконечными пределами; 2) интегралы от неограниченных функций.
Несобственный интеграл от функции f (x) в пределах от a до + ∞ определяется равенством
![]()
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если же предел не существует или равен бесконечности, - расходящимся.
Аналогично
![]() и
и
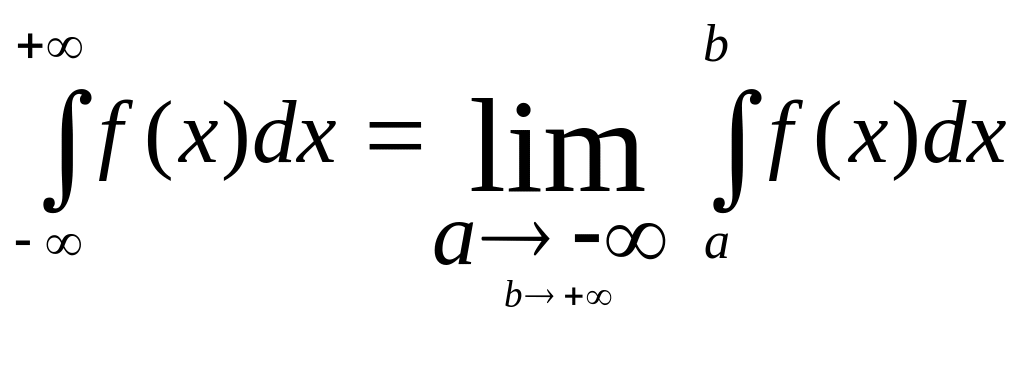
Если функция f(х) имеет бесконечный разрыв в точке с отрезка [а, b] и непрерывна при а ≤ х < с и с < x ≤ b, то, по определению, полагают
![]()
Несобственный
интеграл
![]() (где f(с)=∞,
a
< c
< b)
называется сходящимся,
если
существуют оба предела в правой части
равенства, и расходящимся,
если
не существует хотя бы один из них.
(где f(с)=∞,
a
< c
< b)
называется сходящимся,
если
существуют оба предела в правой части
равенства, и расходящимся,
если
не существует хотя бы один из них.
1567.
Вычислить
несобственный интеграл
![]() (или установить его расходимость).
(или установить его расходимость).
Решение. Имеем
![]()
т. е. предел не существует. Следовательно, несобственный интеграл расходится.
1568.
Вычислить
![]()
Решение. Найдем
![]()
т. е. несобственный интеграл сходится.
1569.
Найти
![]()
Решение.
Подынтегральная функция— четная,
поэтому
![]()
Тогда
![]()
Таким
образом,
![]() ,
т. е. несобственный интеграл сходится.
,
т. е. несобственный интеграл сходится.
1570.
Найти
![]()
Решение. Подынтегральная функция f(х)= 1/х в точке x = 0 неограниченна, а потому имеем
![]()
т. е. несобственный интеграл расходится.
1571.
Найти
![]()
Решение. Имеем
![]()
т. е. несобственный интеграл сходится.
Вычислить несобственные интегралы:
1572.
![]() 1573.
1573.
![]()
1574.
![]() 1575.
1575.
![]() 1576.
1576.
![]()
1577.
![]() 1578.
1578.
![]()
2. Признаки сравнения. При исследовании сходимости несобственных интегралов пользуются одним из признаков сравнения.
1. Если
функции f
(х) и φ(x)
определены для всех х≥а и интегрируемы
на отрезке [а, А], где А≥а, и если
0≤f(х)≤φ(x)
для всех х≥а, то из сходимости интеграла
![]() вытекает
сходимость интеграла
вытекает
сходимость интеграла
![]() ,
причем
,
причем
![]()
2. (а)
Если
при x→+∞
функция
f(x)≥0
является бесконечно малой порядка
р
>
0 по
сравнению с 1/x,
то
интеграл
![]() сходится
при р >
1 и
расходится при р≤1.
сходится
при р >
1 и
расходится при р≤1.
(б) Если функция f(x) ≥0 определена и непрерывна в промежутке а ≤ х< b и является бесконечно большой порядка р по сравнению с1/(b-x) при х→b — 0, то
интеграл сходится при р < 1 и расходится при р≥ а
1579.
Исследовать сходимость интеграла
![]()
Решение. По определению
![]()
Допустим,
что р>1;
тогда
![]() =
0. Значит, при р>1
интеграл
сходится.
Пусть р≤1;
тогда
=
0. Значит, при р>1
интеграл
сходится.
Пусть р≤1;
тогда
![]() ,
т. е. интеграл
при
р≤1
расходится.
,
т. е. интеграл
при
р≤1
расходится.
1580.
Исследовать сходимость интеграла
![]() (интеграл
Френеля).
(интеграл
Френеля).
Решение.
Пусть
![]() ,
тогда
,
тогда
![]() .
Представим
стоящий
справа интеграл в виде суммы:
.
Представим
стоящий
справа интеграл в виде суммы:
![]()
Первое
слагаемое есть собственный интеграл,
так как
![]() ,
а ко второму применим интегрирование
по частям, полагая
,
а ко второму применим интегрирование
по частям, полагая
![]() :
:
![]()
Последний
интеграл сходится, так как
![]() ,
а интеграл
,
а интеграл
![]() сходится.
сходится.
Поэтому
![]() сходится
на основании признака (2а), а следовательно,
данный интеграл также сходится.
сходится
на основании признака (2а), а следовательно,
данный интеграл также сходится.
1581.
Исследовать сходимость интеграла
![]() .
.
Решение.
Подынтегральная функция f(x)=1/(1+x10)
в промежутке интегрирования меньше,
чем φ(х)=1/х10,
а
интеграл
![]() является
сходящимся.
является
сходящимся.
Следовательно, данный интеграл также сходится.
1582.
Исследовать
сходимость интеграла
![]() (a<b).
(a<b).
Решение. По определению
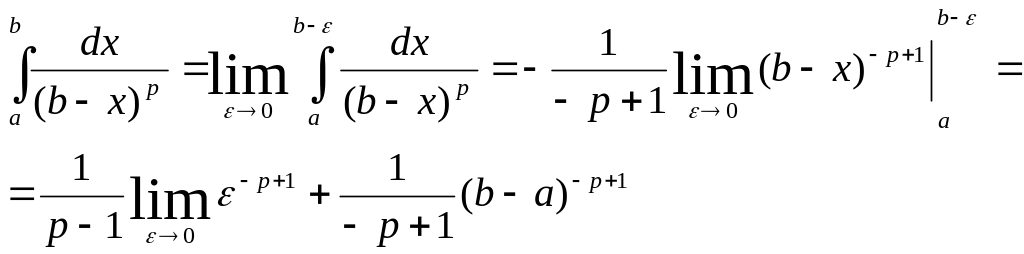
Если
р<1,
то
![]() ;
если же p>
1, то
;
если же p>
1, то
![]() ;
если, наконец, p
= 1 , то
;
если, наконец, p
= 1 , то
![]()
Следовательно,
при р<1
интеграл
![]() сходится, а при р≥1
– расходится.
сходится, а при р≥1
– расходится.
1583.
Исследовать
сходимость интеграла
![]()
Решение. Подынтегральная функция является бесконечно большой при х → 1 . Представим ее в следующем виде:
![]()
т. е. порядок этой бесконечно большой функции при х→1 по сравнению с 1/(1 - x) равен р=1/3 < 1. Поэтому данный интеграл сходится на основании признака (2б).
1584.
Исследовать сходимость интеграла
![]() .
.
Решение.
Подынтегральная функция f(х)
в
промежутке интегрирования положительна
и f
(х) →
∞
при х→0.
Пользуясь
теоремой об эквивалентных бесконечно
малых, преобразуем числитель и знаменатель
подынтегральной дроби: имеем
![]() ,
а
,
а
![]() при х→0,
откуда
при х→0,
откуда
![]()
т. е. f (х) является бесконечно большой порядка р = 2/3 по сравнению с 1/х. Следовательно, по признаку (2б) заданный интеграл сходится.
Исследовать сходимость следующих несобственных интегралов:
1585.
![]() 1586.
1586.
![]() 1587.
1587.
![]()
1588.
![]() 1589.
1589.
![]()
1590.
![]() 1591.
1591.
![]()
