§ 4. Разложение функций в степенные ряды
1.
Ряд Тейлора для функции одной переменной.
Всякая
функция, бесконечно
дифференцируемая в интервале
т.
е. х0-r
< х < х0+r,
может
быть разложена в этом интервале в
сходящийся к ней степенной ряд
Тейлора
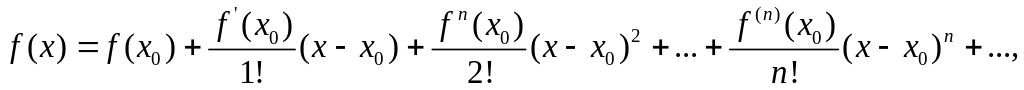
если в этом интервале выполняется условие
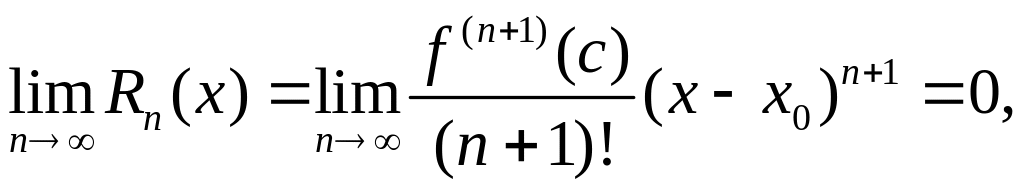
где Rn(х)—остаточный член формулы Тейлора (или остаток ряда), с=х0 +θ(x-х0), 0< θ < 1.
При x0 = 0 получается ряд Маклорена:
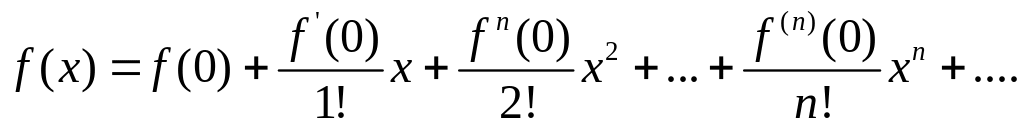
Если
в некотором интервале, содержащем точку
x0,
при любом я выполняется
неравенство |
f(n)
(х) |< М, где
М
—
положительная постоянная, то
и
функция f(х)
разложима
в ряд Тейлора.
Приведем разложения в ряд Маклорена следующих функций:
-∞ <
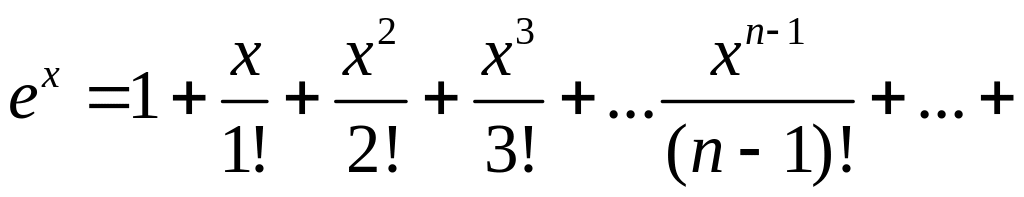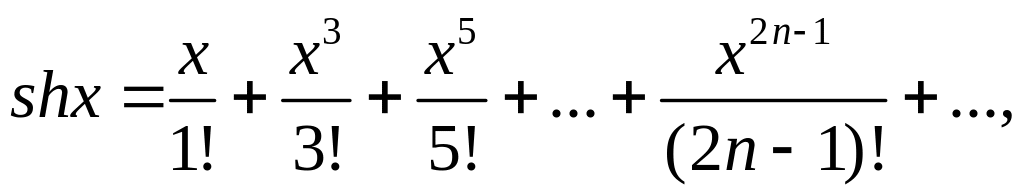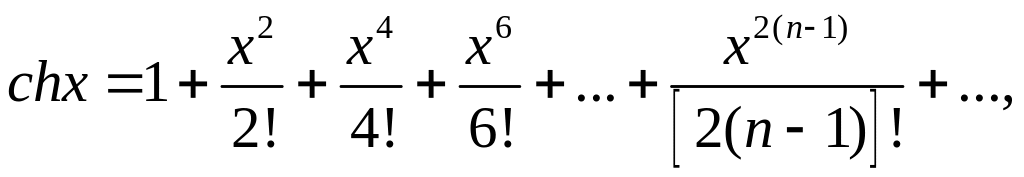x < +∞;
-∞ <
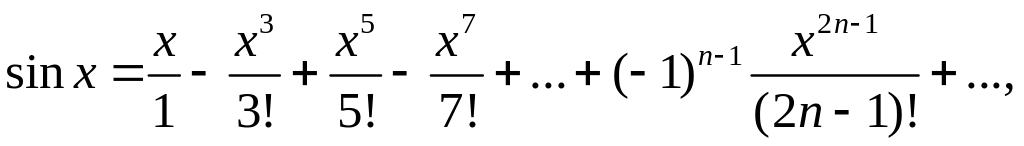x < +∞;
-∞ < x
< +∞;
-∞ <
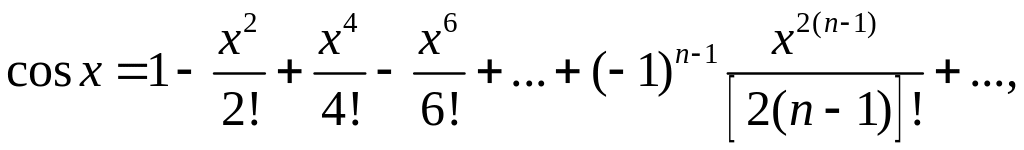x < +∞;
-∞ < x
< +∞;
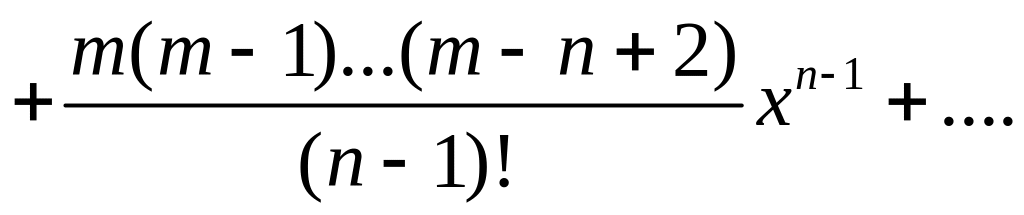
Это последнее разложение имеет место:
при m ≥ 0, если –1 ≤ х ≤ 1;
при -1 < m < 0, если -1 < х ≤ 1;
при m ≤ -1, если -1 < х 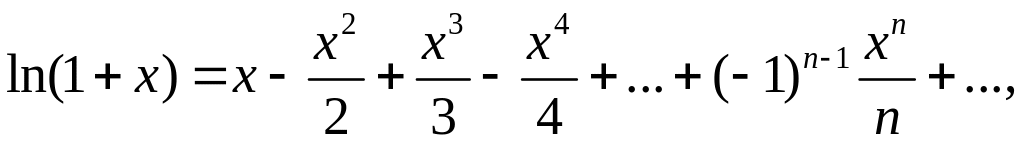< 1;
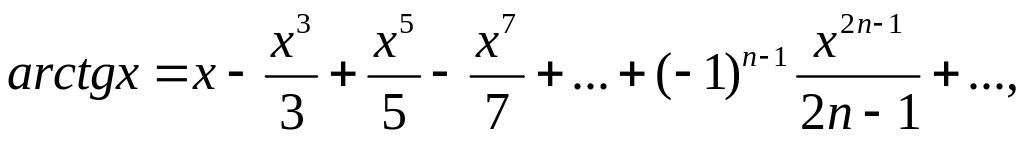-1 <
х ≤ 1;
–1
≤
х
≤
1;
Ряд Тейлора для функции двух независимых переменных. Пусть функция f(х, у) дифференцируема n+1 раз в некоторой окрестности точки Р0 (x0; y0). Тогда в любой точке Р (x; у) из этой окрестности функция f(х, у) может быть разложена в ряд Тейлора:
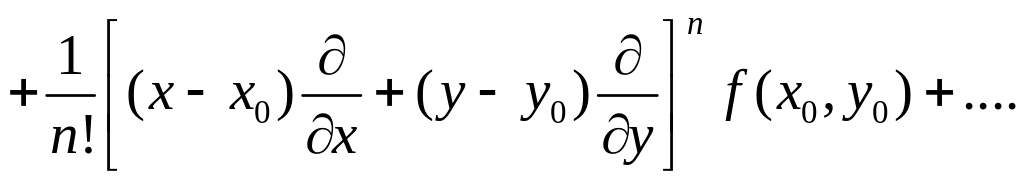
если
в этой окрестности выполняется условие
где
Rn
(х,у)
—
остаток ряда Тейлора.
В частном случае при x0=у0=0 получается ряд Маклорена:
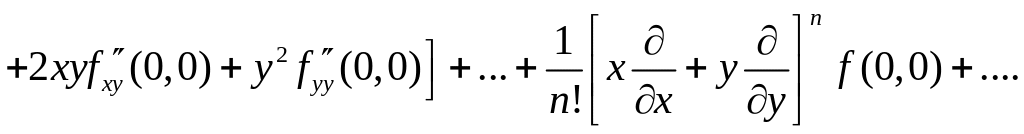
382. Разложить в ряд по степеням х функцию f(x) = 2x. ∆ Найдем значения функции и ее производных при х=0:
f(x)=2x, f(0)=2º=1,
f'(x)=2xln2, f'(0)=ln2,
f''(x)=2xln 22, f''(0)=ln 22,
. . . . . . . . . .
f(n)(x)= 2x·ln n2; f(n)(0)=ln n2.
Так
как 0 < ln 2 < 1, то при фиксированном х
имеет
место неравенство
<2x
для любого
n.
Следовательно, функция может быть
представлена в
виде суммы ряда Маклорена:
В данном случае
-∞
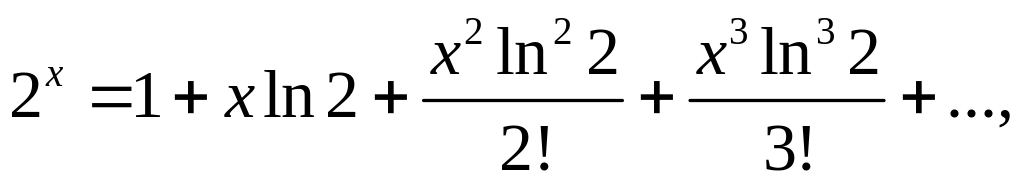< x
< +∞;
Это разложение можно получить и иначе: достаточно в разложении
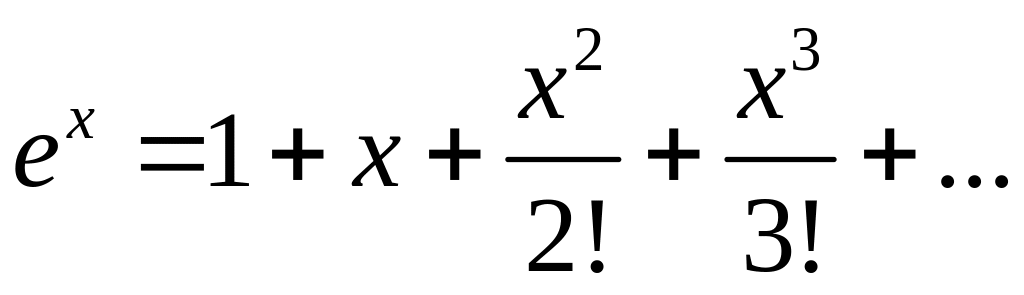
заменить х на xln 2. ▲
Разложить в ряд по степеням х функцию f(х)=sinгх. ∆ Продифференцируем функцию n+1 раз:
f(х)=sinгх,
. . . . . . . . . . . . . . . . .
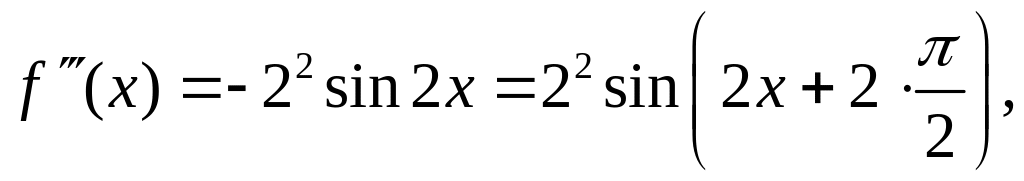
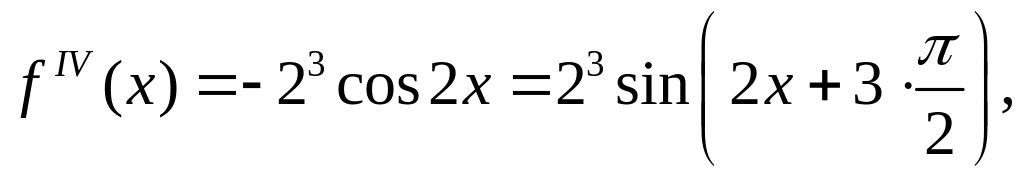
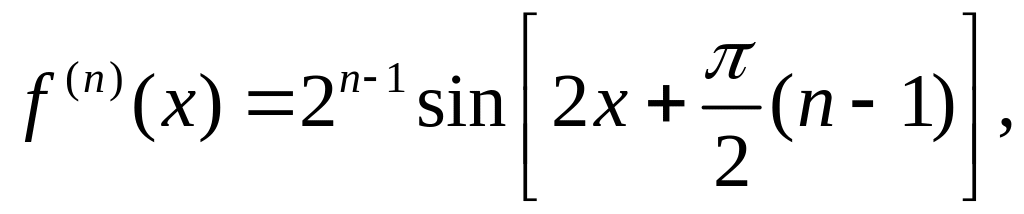
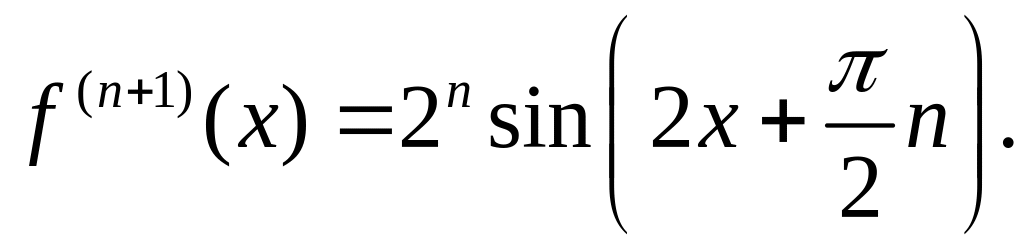
Находим значения функций f(x), f'(x), f"(x), …, f(n)(x) в точке х=0, а значение f(n+1)(x) определяем в точке х=с (см. равенство для определения Rn). Получаем f(0)=0,
f'(0)=0, f"(0)=2, f"'(0)=0, fIV(0)= -23, fV(0)=0, fVI(0)=25, …, f(n+1)(c)=2n ·sin(2c+πn/2).
Находим остаточный член:
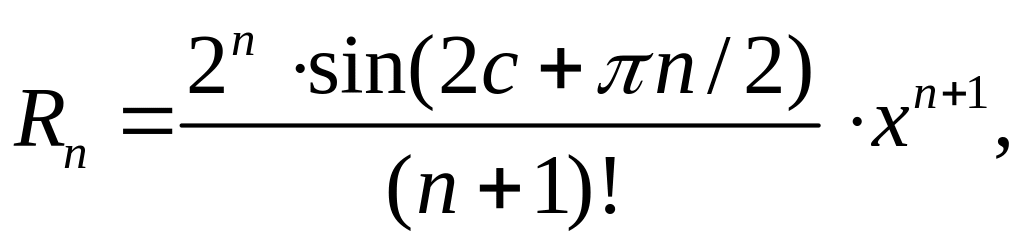т.е.
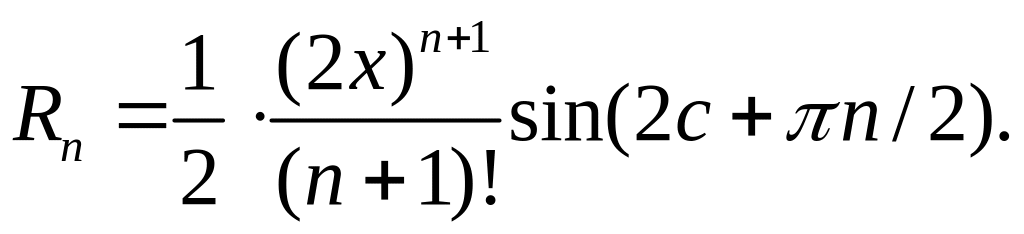
Так
как
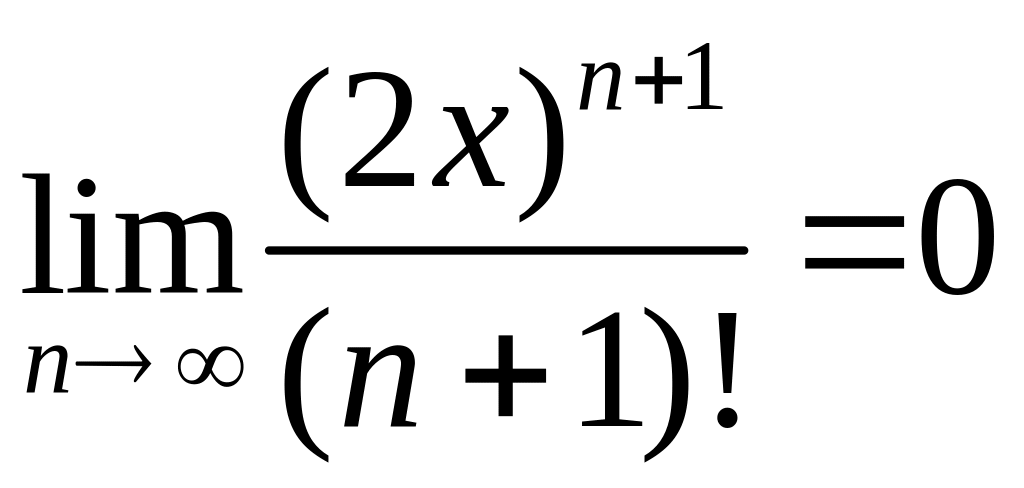при любом х,
а sin(2c+πn/2)
—величина
ограниченная, то
.
Следовательно,
функцию f(x)=sin
2x
можно представить в
виде
суммы ряда Маклорена
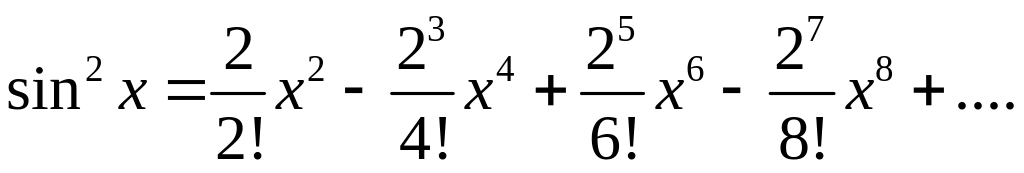
Задачу
можно решить и иначе. В равенстве
заменим
соs2х
его
разложением в степенной ряд:
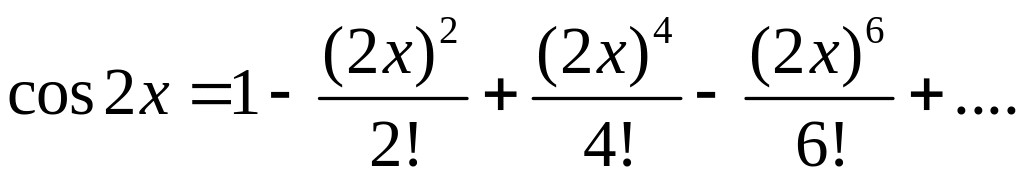
Выполнив несложные преобразования, получим найденное выше разложение sin2x. ▲
384.
Разложить
ряд по степеням х.
∆
В разложении
(-∞
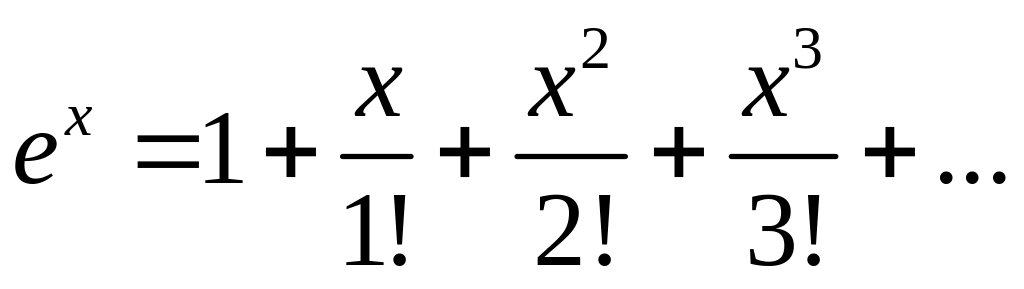< x
< +∞)
заменим х на — х2; получим
(-∞
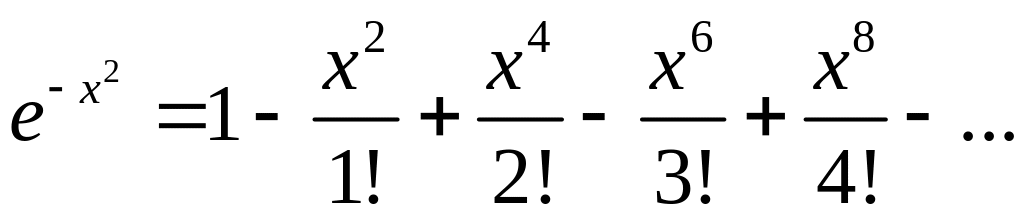< x
< +∞). ▲
385. Разложить lп х в ряд по степеням х—1. ∆ В разложении
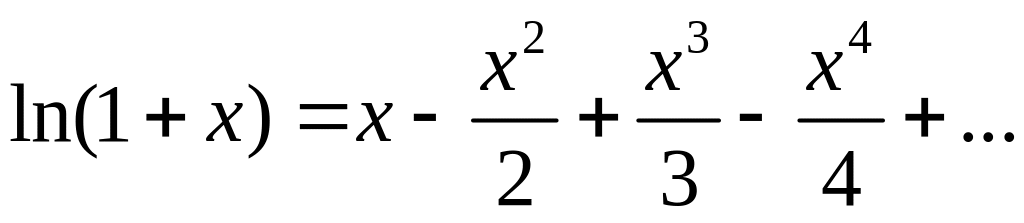( -1< x
≤ 1)
заменим х на х—1; получим
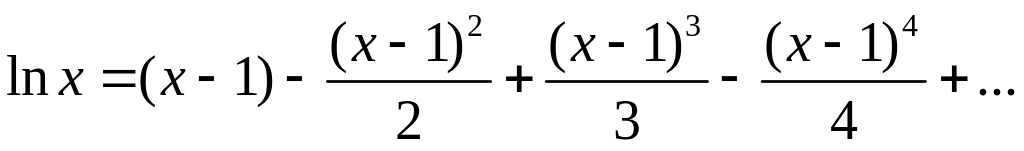( 0 < x
≤ 2).▲
386. Разложить 1/х в ряд по степеням х—2.
∆ Воспользуемся
равенством
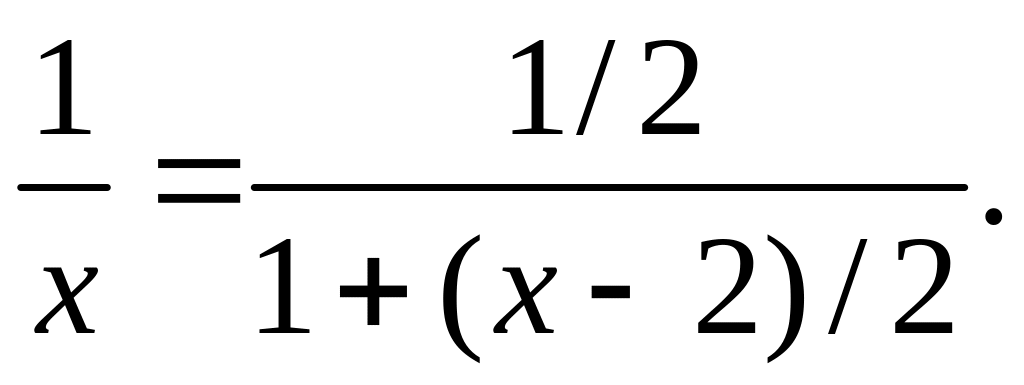Правую часть этого равенства
можно рассматривать как сумму бесконечно
убывающей геометрической
прогрессии с первым членом а
= 1/2
и знаменателем q=
—
(х—2)/2.
Отсюда получаем
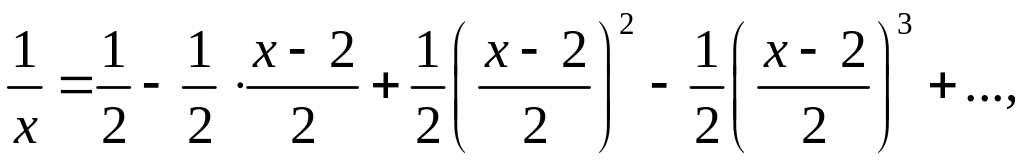
т.е.
Так как | (х—2)/2| < 1, то 0 < х < 4. ▲
387. Разложить в ряд Тейлора функцию f(х,у) = х2—ху+ 2y2— Зх + 4у + 8 в окрестности точки Р0 (—3; 1).
∆ Найдем частные производные и вычислим их значения в точке Р0:
f'x(x,y)=2x-y-3, f'y(x,y)= -x+4y+4, f"xx(x,y)=2, f"xy(x,y)= -1,
f"yy(x,y)=4;
f(-3,1)=35, f'x(-3,1)= -10, f'y(-3,1)=11, f"xx(-3,1)=2,
f"xy(-3,1)= -1, f"yy(-3,1)=4.
Искомое разложение в ряд Тейлора имеет вид
f(х,у) = 35 -10(х+3)+11(у-1) + (х+3)2-(х+3)(у-1) + 2(у-1)2+....▲
388. Разложить в ряд Тейлора функцию f(х, у) = х2lпу в окрестности точки Р0(1; 1) до членов второго порядка.
∆ Найдем частные производные первого и второго порядков:
f'x(x,y)=2хlnу,
f'y(x,y)=
,
f"xx(x,y)=2lny,
f"xy(x,y)=
,
f"yy(x,y)=
Вычислим значения функции и производных в точке Р0(1, 1):
f(1,1)=0, f'x(1,1)=0, f'y(1,1)=1, f"xx(1,1)=0, f"xy(1,1)=2, f"yy(1,1)= -1.
Искомое
разложение записывается
так:
f(x,y)=(y-1)+2(x-1)(y-1)-
(y-1)2+…
. ▲
389. Разложить в ряд Маклорена функцию f(x,y)=cosx shy до членов третьего порядка.
∆ Найдем частные производные первого, второго и третьего порядков:
.
Вычислим значения функции и производных при х0 = у0 = 0:
f(0,0)=0, f'x(0,0)=0, f'y(0,0)=1, f"xx(0,0)=0, f"xy(0,0)=0, f"yy(0,0)=0,
.
Следовательно,
▲
Разложить в ряды по степеням х следующие функции:
390.
391.
392.
393.
394.
a>0.
395.
a>0.
396.
Разложить в ряды Тейлора следующие функции:
397. f(х, у) = х3 — 2у3 + 3ху в окрестности точки Р (2; 1).
398. f(x,y)=4x3 - x2 + 2xy - y2 + 5х + у—8 в окрестности точки Р (1; —1).
399. f (х, у) = 5x2 + 9у2—2х + 3у—5 в окрестности точки Р(1; -1).
f(х, у) = х/у в окрестности точки Р(—1; 1) до членов третьего порядка.
401. f(х, у) = хе-y в окрестности точки Р(1; 0) до членов второго порядка.
402. f(х, у) = хсоs2у в окрестности точки Р(—1; 0) до членов третьего порядка.