§ 2. Функциональные ряды

Ряд

члены которого—функции от х, называется функциональным. Совокупность значений х, при которых функции и₁(х), и₂(х), ..., u_n(x)... определены и ряд 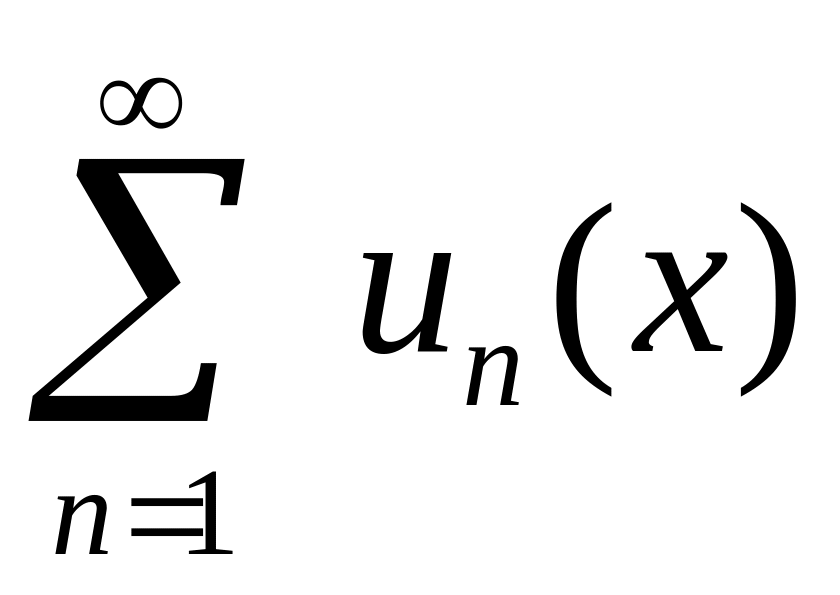сходится, называют областью сходимости функционального ряда. Областью сходимости функционального ряда чаще всего служит какой-нибудь промежуток оси Ох. Каждому значению из области сходимости X соответствует определенное значение величины Эту величину, являющуюся функцией х, называют суммой функционального ряда и обозна­чают через S(х).

Представим сумму ряда в виде S(х) = S_n(х)+R_п (х), где

[R_n(x)— остаток функционального ряда].

Сходящийся функциональный ряд называется равномерно сходящимся в некоторой области X, если для каждого сколь угодно малого числа δ > 0 найдется такое целое положительное число N, что при п≥N выпол­няется неравенство /R_n (х)/ <δ для любого х из области X. При этом сумма S (x) равномерно сходящегося ряда в области X, где и_n (х) (п=1, 2, 3, ...)—непрерывные функции, есть непрерывная функция.

Сформулируем достаточный признак равномерной сходимости функцио­нального ряда — признак Вейерштрасса.

Если функции и₁(х), и₂(х), …, и_п(х), ... по абсолютной величине не превосходят в некоторой области X положительных чисел а₁, а₂, ...,а_n, ..., причем числовой ряд

a₁+a₂+a₃+…+a_n+…

сходится, то функциональный ряд

в этой области сходится равномерно.

В заключение сформулируем две теоремы, относящиеся к интегрированию и дифференцированию функциональных рядов.

1. Если , где u₁ (x), и₂(х), ..., и_n (х), ... —непрерывные функции, равномерно сходится в некоторой области X и имеет сумму S (х), то ряд

сходится и имеет сумму 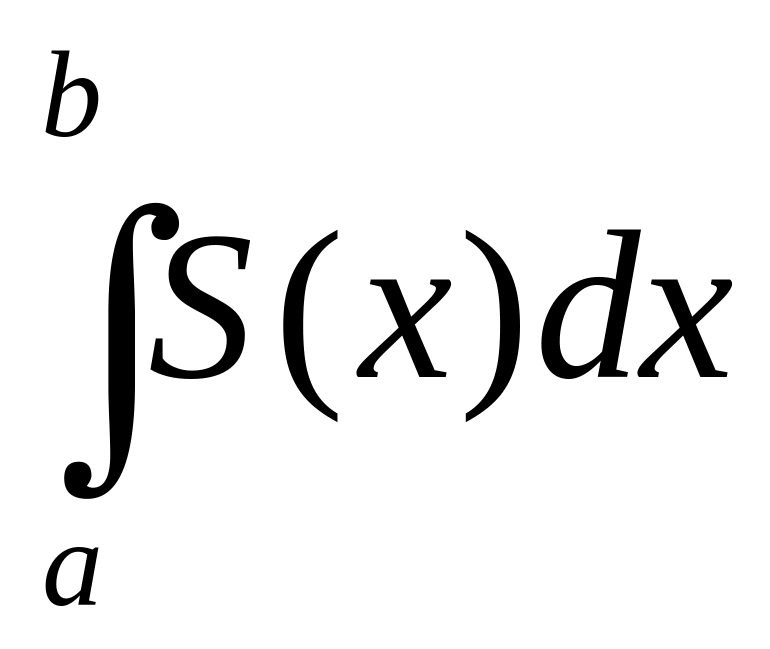(промежуток [а, b] принадлежит области X).

2. Пусть функции 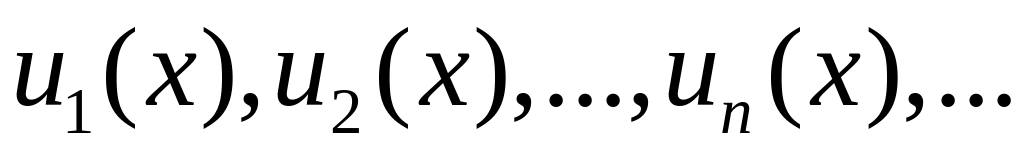определены в некоторой области X и имеют в этой области производные

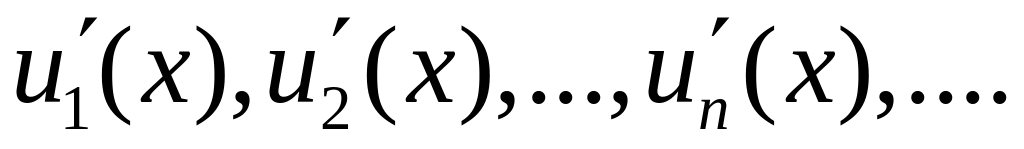
Если в этой области ряд сходится равномерно, то его сумма равна производной от суммы первоначального ряда:

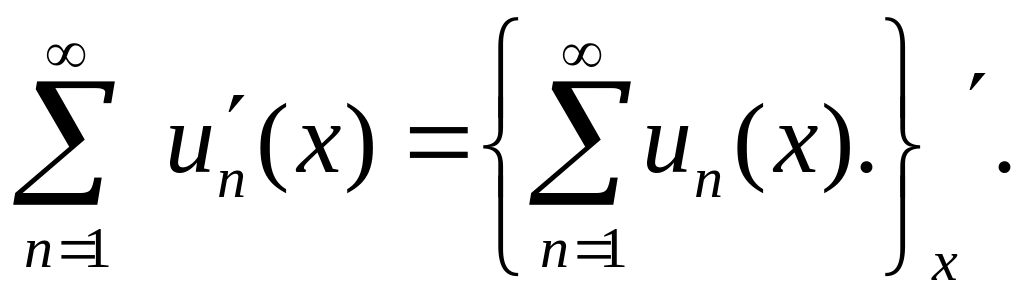
338. Дан функциональный ряд

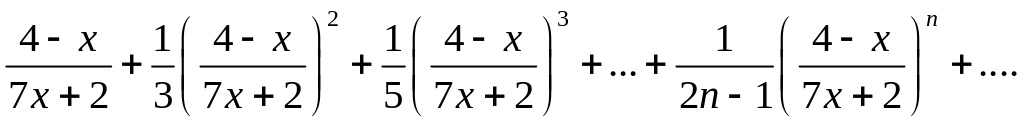
Исследовать сходимость ряда в точках х=0 и х=1.

∆ В точке х=0 получаем ряд

Здесь u_n= 2ⁿ/(2n—1), u_n+1 = 2ⁿ⁺¹/(2n+1). Применяем признак Даламбера:

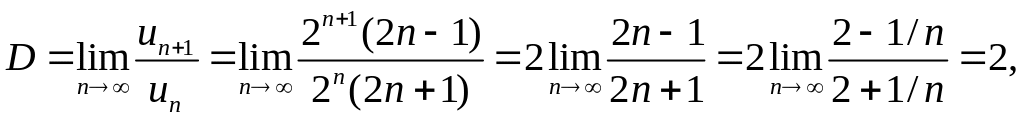
т. е. D > 1. Следовательно, ряд расходится.

В точке х=1 получаем ряд

Здесь находим

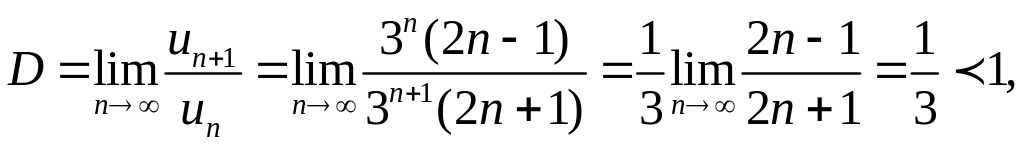
т. е. ряд сходится. ▲

338. Найти область сходимости ряда

∆Если |x|< 1, то ; так как

ряд расходится. Если |x|=1, то также получаем расходящийся ряд

Если |х| > 1, то члены заданного ряда меньше членов бесконечно убы­вающей геометрической прогрессии т.е. ряд сходится.

Итак, область сходимости ряда определяется неравенством |д;|> 1. От­сюда следует, что ряд сходится, если 1 < x < +∞ или —∞ < х < —1. ▲

338. Показать, что ряд

сходится равномерно при всех значениях х(-∞<x<∞).

∆ Данный ряд при любом значении х сходится по признаку Лейбница, поэтому его остаток оценивается с помощью неравенства |R_п(х)| < |и_п+1(х)|, т. е.

Так как неравенства и равносильны, то, взяв , где

N—какое-нибудь целое положительное число, удовлетворяющее условию , приходим к неравенству |R_п(х)| < . Итак, данный ряд сходится

равномерно в промежутке (—∞, +∞). ▲

341. Показать, что ряд сходится неравномерно в ин-

тервале (—1, 1).

Δ В указанном интервале ряд сходится как бесконечно убывающая гео­метрическая прогрессия. Имеем , т. е. .

Но , . Следовательно,

приняв <1/2, мы не сможем добиться выполнения неравенства при любом

значении х. Итак, ряд сходится неравномерно. ▲

338. С помощью признака Вейерштрасса показать, что ряд

сходится равномерно в промежутке (—∞, +∞).

Δ Так как и ряд сходится, то дан-

ный ряд сходится равномерно при любых значениях х. ▲

343. Можно ли к ряду

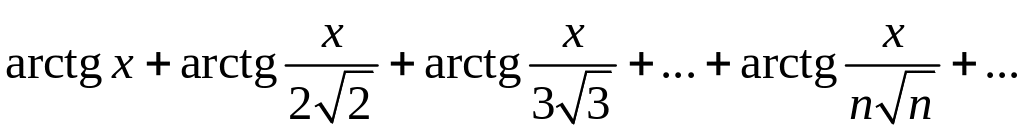
применить теорему о почленном дифференцировании рядов?

Δ Сравним данный ряд со сходящимся рядом

(при любом фиксированном х). Тогда , .

Так как и — эквивалентные бесконечно малые, то 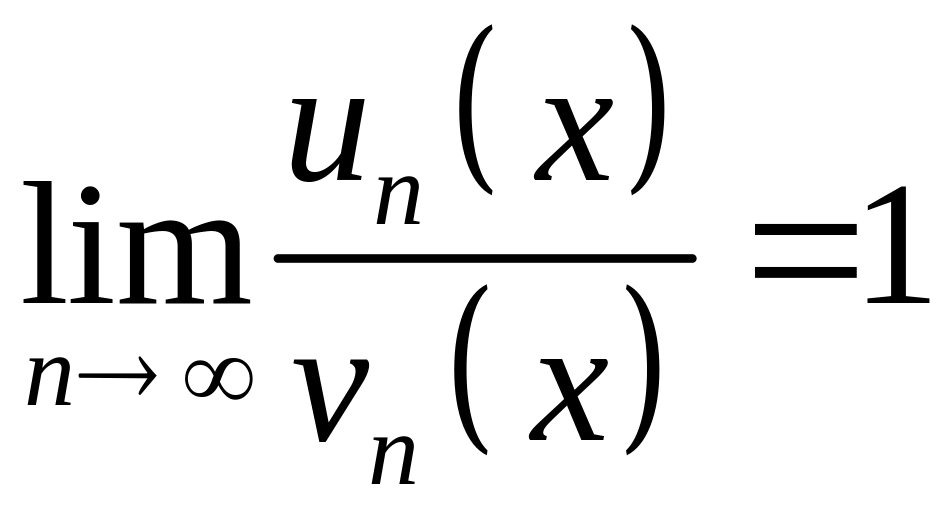и

согласно второму признаку сравнения заключаем, что данный ряд сходится. Найдем производную общего члена данного ряда:

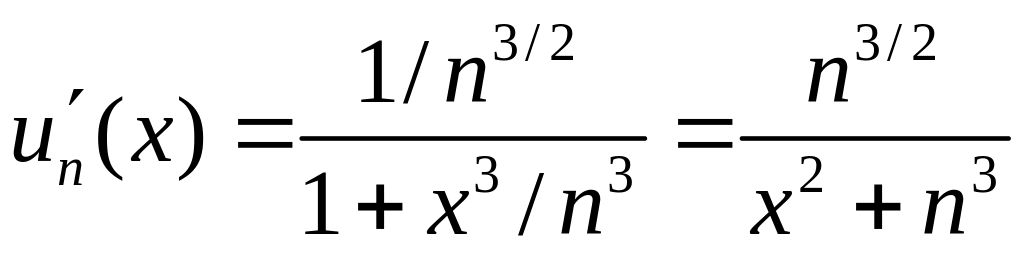
Ряд, составленный из производных, имеет вид

Заметим, что члены последнего ряда меньше соответствующих 'членов сходящегося ряда Поэтому на основании признака Вейерштрасса ряд, составленный из производных, равномерно сходится в про­межутке (—∞, +∞) и, значит, к заданному ряду можно применить теорему о дифференцировании рядов. ▲

343. Законно ли применение к ряду

теоремы об интегрировании функциональных рядов в промежутке ?

Δ Члены заданного ряда при любом значении х по абсолютной величине меньше соответствующих членов бесконечно убывающей геометрической прог­рессии Поэтому данный ряд согласно признаку Вейершт­расса равномерно сходится в промежутке (—∞, +∞) и, следовательно, к нему можно применить теорему об интегрировании рядов для любого конеч­ного промежутка [а, b], в частности, для промежутка . ▲

343. Дан функциональный ряд

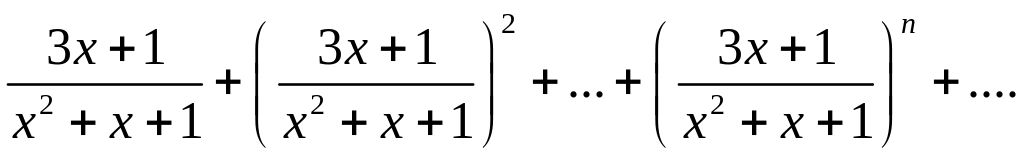
Сходится ли ряд в точках х=1, х=2 и х=3?

343. Исследовать сходимость функционального ряда

в точках x:=1 и х=2.

343. Найти область сходимости ряда

348. Найти область сходимости ряда

343. Найти область сходимости ряда

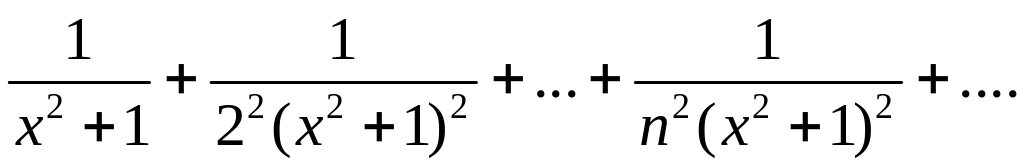
350. Показать, что ряд 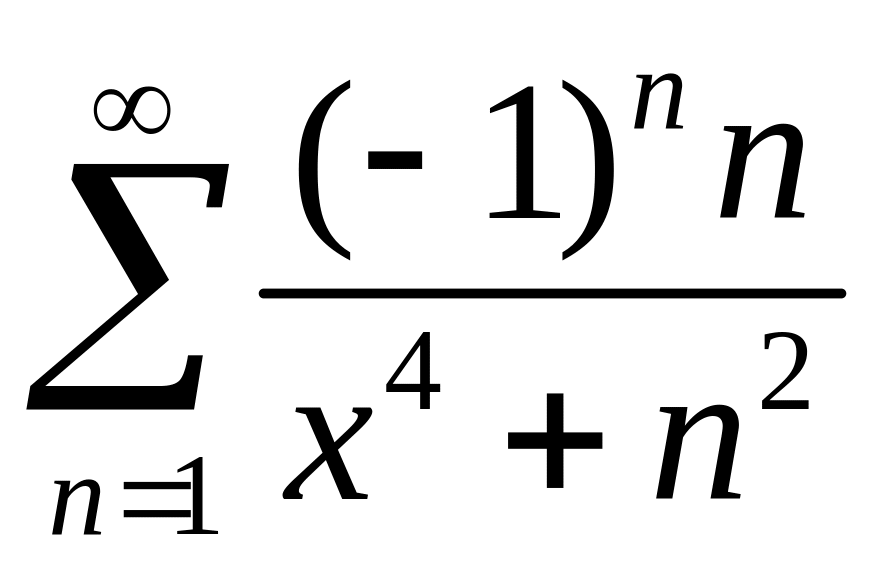равномерно сходится в

промежутке (—∞, +∞).

351. Показать, что ряд

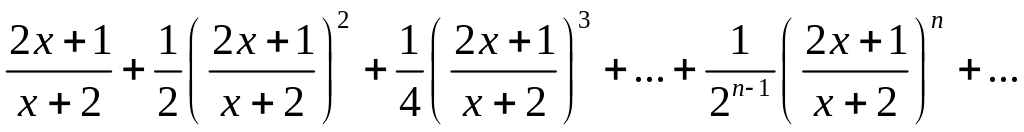
равномерно сходится в промежутке [—1, 1].

352. Показать, что ряд

в интервале (—2, 2) сходится неравномерно.

353. Показать, что ряд

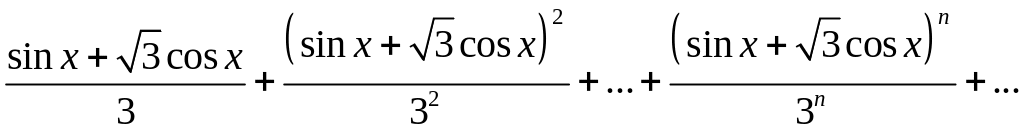
сходится в промежутке(—∞, +∞) и установить характер схо­димости.

354. Можно ли к ряду

применить теорему о дифференцировании функциональных рядов?

355. Можно ли к ряду

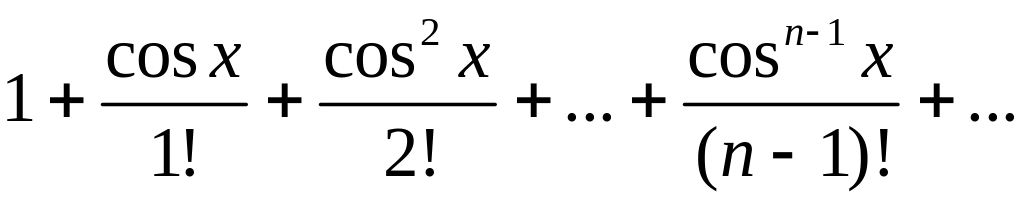
применить теорему об интегрировании функциональных рядов в любом конечном промежутке [а, b]?

356. Можно ли к ряду

применить теорему о дифференцировании функциональных рядов?