1.Первообразная и неопределенный интеграл. Свойства неопределенного интеграла

Первообразная и неопределенный интеграл

Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).

Обозначение

где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.

Свойства неопределенного интеграла

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

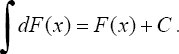
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

3. Метод замены переменной в неопределенном интеграле

Найти неопределенный интеграл.

Проведем замену:   

Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.

Найти неопределенный интеграл. 

Замена:  Осталось выяснить, во что превратится  Хорошо,   мы выразили, но что делать с оставшимся в числителе «иксом»?! Время от времени в ходе решения интегралов встречается следующий трюк:   мы выразим из той же замены  !

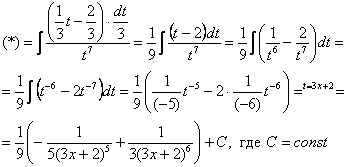
4. Метод интегрирования по частям в неопределённом интеграле

Функции   и   гладкие, следовательно, возможно дифференцирование:

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

Операция интегрирования обратна дифференцированию:

После перестановок:

Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во времяинтегрирования.

Типичную ошибку «потери» константы при обращении с неопределенным интегралом иллюстрирует следующий пример-софизм:

Отсюда «следствие»:  , что очевидно неверно.

• 

• 

5. Определение интеграла его свойства

Определение. Пусть  . Пусть  ,   аддитивна, и ее плотность равна  . Тогда   называется интегралом.

Обозначение. Пусть  . Значение функции   на отрезке  :

Теорема (Ньютон, Лейбниц). Пусть  ,   – первообразная функции  . Тогда 

Доказательство. По теореме о плотности аддитивной функции промежутка,   и равна плотности функции  . По определению тогда   – интеграл функции  .

Свойства интеграла

1. 

2.  .

Доказательство. Пусть   - первообразная  ,   – первообразная  . Тогда   – первообразная  .

6. Механический и геометрический смысл определенного интеграла

Механический смысл определенного интеграла

Пусть материальная точка М перемещается под действием силы , направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х – абсцисса движущейся точки М.

Найдем работу А силы по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (a < b). Для этого отрезок [a; b] точками а = х₀, х₁, ..., b = х_n (х₀< х₁<...< х_n) разобьем на n частичных отрезков [х₀; х₁], [х₁; х₂], ..., [х_n-1; х_n]. Сила, действующая на отрезке [х_i-1; х_i], меняется от точки к точке. Но если длина отрезка Δх_i = х_i – х_i-1 достаточно мала, то сила на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = c_i [х_i-1; х_i]. Поэтому работа, совершенная этой силой на отрезке [х_i-1; х_i], равна произведению F(c_i)∙Δх_i. (Как работа постоянной силы F(c_i) на участке [х_i-1; х_i]).

Приближенное значение работы А силы на всем отрезке [a; b] есть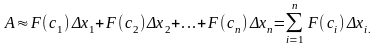

Это приближенное равенство тем точнее, чем меньше длина Δх_i. Поэтому за точное значение работы А принимается предел суммы при условии, что наибольшая длина λ частичных отрезков стремится к нулю:

.

Итак, работа переменной силы , величина которой есть непрерывная функция F = F(x), действующая на отрезке [a; b], равна определенному интегралу от величины F(x) силы, взятому по отрезу [a; b].

В этом состоит механический смысл определенного интеграла.

Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от t = a до t = b, равен определенному интегралу от скорости v(t):

масса т неоднородного стержня на отрезке [a; b] равна определенному интегралу от плотности

γ(х):

Геометрический смысл определенного интеграла

Понятие определенного интеграла введено таким образом, что в случае, когда функция y = f(x) неотрицательна на отрезке [a; b], где a < b,

численно равен площади S под кривой y = f(x) на [a; b] (рис. 3).

Действительно, при стремлении к нулю ломаная (рис. 4) неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.

Учитывая сказанное, можно указать значения некоторых интегралов, используя известные планиметрические формулы для площадей плоских фигур. Например,

и т.д.

(Первый из интегралов – площадь квадрата со стороной единичной длины; второй – площадь прямоугольного треугольника, оба катета которого единичной длины; третий – площадь четверти круга единичного радиуса).