2. Дискриминантный анализ

Дискриминантный анализ позволяет проверить гипотезу о возможности классификаций заданного множества объектов n, характеризуемых некоторым числом t переменных показателей x,на некоторое число классов или кластеров k дать классификации вероятностную оценку.

При выполнении анализа ищется набор дискриминирующих функций , обеспечивающих классификацию объектов на заданное число классов:

Классы нумеруются натуральными числами i от 1 до k, где k – число классов.

i=1 ,…., k.

Исходные данные представляются в виде матрицы размером (t+1) n, причем n строк характеризуется n объектов. Первые t столбцов – это значение t переменных для n объектов, а (m+1) столбец для каждого объекта – это номер его класса. Классы нумеруются натуральными числами от 1 до k, где k – число классов. Если нужно классифицировать ряд новых объектов, то такие объекты также включаются в матрицу данных с номером класса 0.

Результаты анализа представляют собой следующие оценки:

1) суммарное межкластерное расстояние Махаланобиса D² с уровнем значимости P для нулевой гипотезы «D² = 0», т.е. гипотезы о невозможности разбиения совокупности объектов на заданное число классов;

2) коэффициенты дискриминирующей функции, обеспечивающие отнесение объектов к данному классу;

3) данные для каждого объекта j, в том числе номер его класса r, расстояние Махаланобиса D_j² от объекта до центра класса, уровень значимости P нулевой гипотезы «D_j²=0», т.е. гипотезы о том, что объект может быть отнесен к данному классу, а также вероятность P_jr отнесения объекта к этому классу.

Если P > 0,05, то соответственно нулевая гипотеза может быть принята; иначе – отвергнута.

3.Факторный анализ (метод главных компонент)

Переменные, значения которых представляют собой статистические данные или результаты социологических исследований, опросов потребителей и экспертов, нередко носят условный характер и не отражают сущность реальных факторов, влияющих на исследуемый процесс (потребительский выбор или величину спроса). К тому же нередко наблюдается линейная зависимость (мультиколлинеарность) между ними. Число независимых (реальных), часто первоначально скрытых, факторов, может быть существенно меньше, чем число исходных показателей. Возникает задача – сократить число переменных до нескольких, наиболее существенных факторов, позволяющих объяснить изменения результативного показателя. Чаще всего для этой цели используется метод главных компонент.

Суть вычислений по методу главных компонент заключается в следующем:

Строится матрица, элементами которой являются отклонение результатов наблюдений над n переменными от соответствующих средних

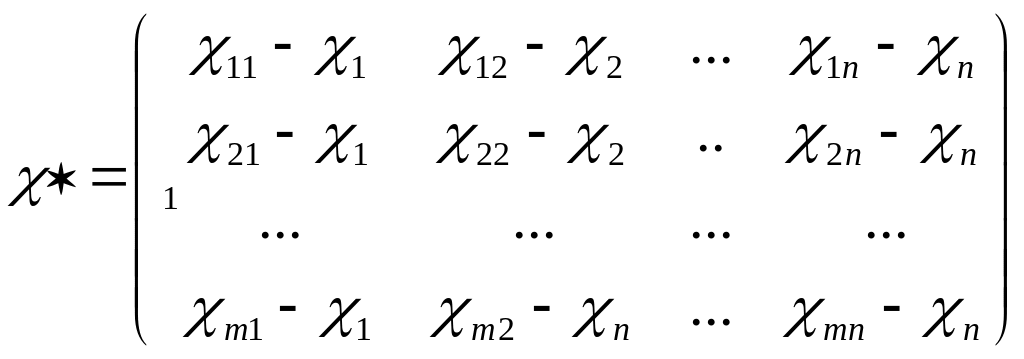
Определяется матрица дисперсий и ковариаций объясняющих переменных:

Матрица S_xx имеет размерность n x n.

Главные компоненты z_j (j=0,…,n) являются линейными комбинациями объясняющих переменных x_j^* (j=0,…, n) и могут быть записаны в общем виде как

.

Они удовлетворять упомянутому выше требованию: каждый раз выделенная главная компонента должна воспроизводить максимум дисперсий. На неизвестные векторы коэффициентов a_j накладываются дополнительные ограничения:

(т.е. они должны быть нормированы) и

(т.е. они должны быть некоррелированы).

Дисперсия главной компоненты z_j

должна принимать наибольшее значение при перечисленных соблюдении условий. Для решения проблемы максимизации функции, связанной дополнительными ограничениями, пользуются методом множителей Лагранжа. В конечно итоге задача сводится к определению собственных значений матрицы S_xx и соответствующих собственных векторов a_j.

Собственные значения матрицы S_xx определяются из уравнений, которые в общем виде записываются как

,

где - множители Лагранжа; I – единичная матрица.

Подставляя последовательно собственные значения, начиная с наибольшего, в уравнение

получим собственные векторы матрицы S_xx, соответствующие этим собственным значениям. Собственные векторы затем используются для построения искомых векторов коэффициента в формуле

Так как собственные векторы известны, по формуле можно определить главные компоненты. При этом обычно довольствуются меньшим, чем n, числом главных компонент, но достаточным, чтобы воспроизвести большую часть дисперсий. По мере выделения главных компонент прекращают в тот момент, когда собственные значения соответствующие каждый раз наибольшим дисперсиям, становятся пренебрежимо малыми. Количество выделенных главных компонент r в общем случае значительно меньше числа объясняющих переменных m. По r главным компонентам строится матрица Z. С помощью главных компонент оцениваются параметры регрессии

И вычисляются значения регрессии

При всех своих преимуществах (уменьшение высокой мультиколлинеарности объясняющих переменных) метод главных компонент обладает и недостатками.

Во-первых, главным компонентам, как правило, трудно подобрать экономические аналоги. Поэтому вызывает затруднения экономическая интерпретация оценок параметров регрессии, полученных по приведенным формулам. Во-вторых, оценки параметров регрессии получают не по исходным объясняющим переменным, а по главным компонентам. В итоге можно сказать, что метод главных компонент применяется в основном для оценки значений регрессии и для определения прогнозных значений зависимой переменной, что также является целью регрессионного анализа.

Заключение.

Таким образом, на лекциях за 3й семестр студенты получили возможность ознакомиться с основными положениями теории статистики, с методами сбора и обработки статистической информации, различными видами статистических показателей, а также методами оценки характера распределения, методами оценки степени тесноты статистических взаимосвязей, методами анализа динамики и построения уравнений тренда и уравнений регрессии.

В следующем семестре изучается прикладная социально-экономическая статистика и статистика финансов – новая для нашей страны область статистики.

1 От англ. слова represent – представлять.

2 Это свойство используется для расчета средней арифметической в том случае, если не известны частоты отдельных значений признака, а известны только их удельные веса (доли) в общей численности статистической совокупности.

3 Эту тему я обычно не читаю ни вечерникам ни заочникам, так как она имеет относительно узкое практическое применение.

4 В настоящее время в г.Москве положение значительно улучшилось, рождаемость превышает смертность.

5 Эту тему для вечерников я сочла нужным убрать, так как по-моему все эти формулы изучаются еще в математической статистике.

6 Альтернативный признак – признак, у которого только два значения (условно измеряемые нулем и единицей). Например, пол человека может быть женским (0) или мужским (1). Обычно с помощью понятия «альтернативный признак» измеряется наличие (1) или отсутствие (0) какого-либо качественного признака (например, наличие высшего образования у человека). Любой вопрос в анкете (статистическом формуляре), на который можно дать только два варианта ответа «да» или «нет», также относится к альтернативным признакам опрашиваемых (например, «Жилая площадь Вашей квартиры менее 30 м или нет?»).

7 Слово «корреляция» происходит от английского слова «correlation» (т.е. отношение или соотношение).

8 Различные виды и способы построения уравнений регрессии рассматриваются на следующей лекции.

9 Более подробный перечень таких показателей изучается в курсе эконометрики.

10 Более подробно расчет корреляционного отношения расчет рассматривается на следующей лекции.

11 Слово regression по-английски означает «связь». Подробнее построение уравнений регрессии рассматривается на следующей лекции

1 Более подробно эти виды функций и методы расчета их параметров обычно изучают в курсе эконометрики.

12 Более подробно эти методы изучаются в дисциплине «Эконометрика»