Лекция №10. Построение уравнений тренда и уравнений парной линейной регрессии

Введение

На предыдущей лекции мы говорили о сглаживании динамических рядов и о том, что аналитическое сглаживание осуществляется на основе так называемых уравнений тренда. А перед этим, изучая методы анализа статистических взаимосвязей, мы говорили о построении так называемых уравнений регрессии. На самом деле между уравнениями тренда и уравнениями регрессии имеется немало общего и для расчета их параметров используется один и тот же метод наименьших квадратов (МНК). Разница лишь в том, что уравнения тренда выражают зависимость некоторого показателя от времени, а уравнения регрессии – статистическую зависимость между двумя и более показателями. На данной лекции мы будем более подробно изучать построение этих уравнений с помощью разработанного в математической статистике метода (МНК). И прежде всего кратко рассмотрим сущность этого метода.

1. Сущность метода наименьших квадратов

Этот метод более подробно изучается в математической статистике и в эконометрике.

Его сущность заключается в том, что параметры аналитической функции, используемой для сглаживания ряда, подбираются таким образом, чтобы минимизировать сумму квадратов отклонений расчетных (теоретических) значений динамического ряда от фактических (исходных) значений. То есть находится:

,

где - фактические значения показателя (исходные статистические данные), а - расчетные значения (полученные на основе построенного уравнения тренда или регрессии). Например, для уравнения линейного тренда такая сумма квадратов имеет вид:

Так как значения и нам известны, то сумма квадратов в действительности является функцией многих переменных, в качестве которых выступают неизвестные значения параметров уравнений тренда (или регрессии).

= Q (a₀, a₁, a₂,… a_n)

Таким образом, задача поиска параметров функций, сглаживающих исходный ряд, преобразуется в задачу поиска min Q (a₀, a₁, a₂,… a_n).

Как известно из высшей математики, задача поиска экстремума (минимума или максимума) некоторой функции обычно решается путем ее дифференцирования и приравнивания частных производных к нулю.

Точно так же данная задача решается и в этом случае. Находятся частные производные функции Q (a₀, a₁, a₂,… a_n) по каждому из параметров и приравниваются к нулю. Получается система уравнений, в которой число неизвестных и параметров совпадает с числом параметров, которые необходимо найти. Эта система в статистике называется системой «нормальных уравнений». В зависимости от вида конкретного уравнения тренда или регрессии эти системы имеют разный вид.

2. Построение уравнений регрессии

Уравнение регрессии – это уравнение, выражающее статистическую зависимость между различными показателями.

В зависимости от того, сколько различных факторов (показателей) связаны этой зависимостью, разделяют уравнения парной и множественной регрессии.

Уравнение парной регрессии выражает связь между двумя признаками (или показателями), один из которых (независимый) называется факторным, а второй (зависимый) – результативным.

Уравнение множественной регрессии выражает зависимость между более чем двумя показателями, один из которых называется результативным (обозначается обычно через y, а остальные факторными: обозначаются x₁, x₂, x₃,…).

Уравнения парной регрессии могут иметь различный вид, в зависимости от того, какой функцией эта зависимость выражается (линейной, параболой и т.п.): Чаще всего используются следующие функции:

линейная y_x = a₀ + a₁x;

полулогарифмическая y_x = a₀ + a₁lgx;

показательная y_x = a₀ + a₁^x;

степенная y_x = a₀ x^a1;

гиперболическая y_x = a₀ + a₁ .

Для расчета параметров уравнений регрессии используется рассмотренный выше метод наименьших квадратов.

Параметры уравнения регрессии находятся путем решения так называемых систем «нормальных уравнений», которые имеют разную форму для уравнений регрессии различного вида (в зависимости от числа переменных и вида функциональной зависимости между показателями).

Остановимся вначале более детально на расчете параметров уравнения парной линейной регрессии, так как для расчета его параметров непосредственно выведены формулы, которые нетрудно использовать на практике.

Предположим, что имеется два ряда значений исходных показателей x и y (факторного и результативного признаков). Требуется построить уравнение парной линейной регрессии между признаками:

y = a₀ + a₁x.

Для определения его параметров составляется система нормальных уравнений:

n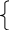 a₀ + a₁Σx = Σy;

a₀Σx + a₁Σx² = Σxy. (10.1)

Для решения системы обычно используется метод определителей.

Рассчитывается определитель матрицы коэффициентов при неизвестных, т.е. определитель

Δ =

Затем поочередно вместо каждого столбца этой матрицы подставляется столбец свободных членов и рассчитывают еще два определителя:

Δ₀ =

Δ₁ =

Находим неизвестные и по формулам:

= Δ₀/ Δ и = Δ₁/ Δ

В результате получаем следующие формулы для расчета параметров уравнения регрессии:

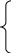
(10.2)

Чтобы воспользоваться приведенными выше формулами, обычно строится вспомогательная таблица (табл. 10.1), в последней строке которой находятся величины , , , , которые необходимо подставить в формулы (11.2).

Таблица 101.1