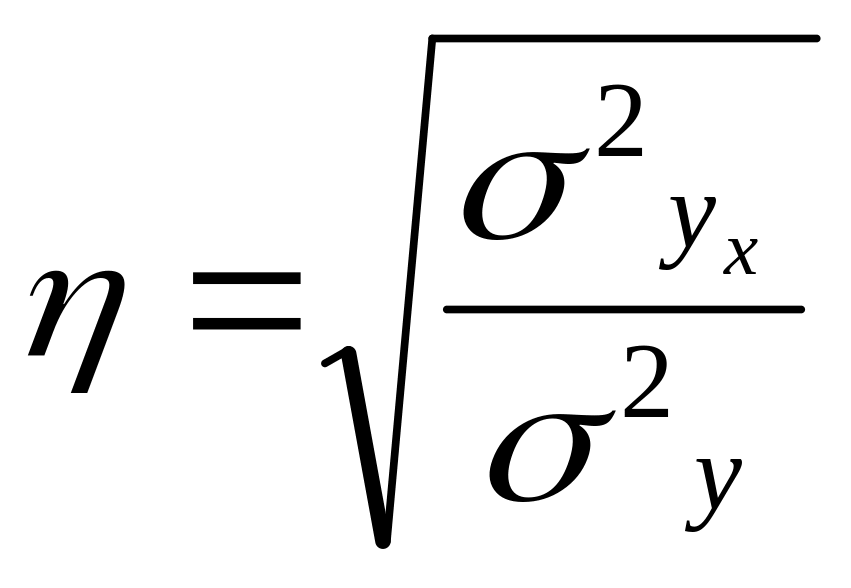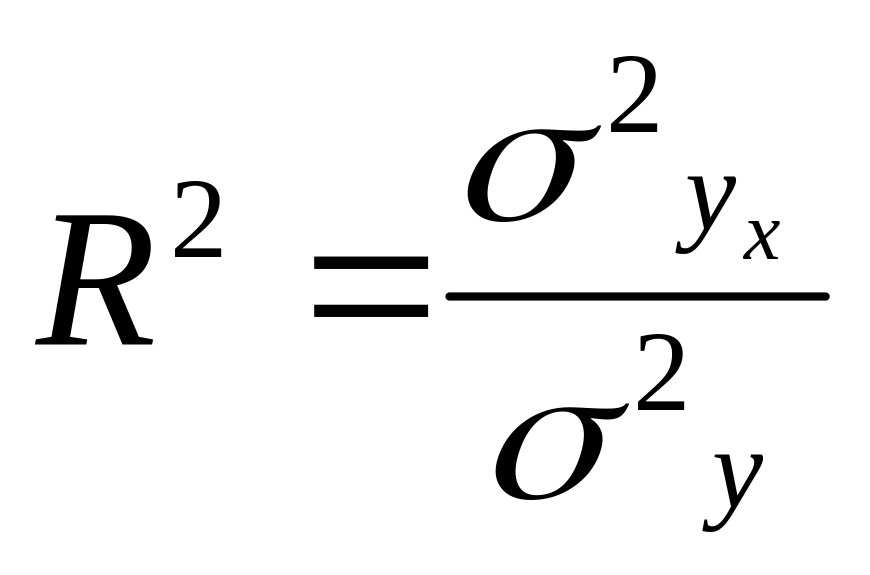- •Три этапа развития статистики
- •Основные этапы развития статистики
- •2. Предмет и задачи статистики
- •3.Основные понятия теории статистики
- •Сбор информации;
- •1.Организационные и методологические вопросы статистического наблюдения
- •2. Ошибки статистического наблюдения
- •Классификация ошибок статистического наблюдения
- •3. Организационные формы, виды и способы статистического наблюдения
- •1. Сводка и группировка (понятие и основные виды)
- •2.Ряды распределения: атрибутивные и вариационные
- •3.Статистические таблицы и графики, требования к составлению таблиц
- •Макет таблицы
- •4. Классификация как особый вид группировки. Роль классификаций в статистике
- •2. Классификация относительных показателей
- •Классификация относительных показателей
- •3. Понятие «средняя величина» и основные виды средних величин в статистике Понятие «средняя величина»
- •Различные виды средних величин и способы их расчета
- •В табл. 4.2 те же обозначения, что и в табл. 4.1.
- •Вспомогательная таблица для расчета простой и взвешенной средней арифметической
- •Исходные данные и вспомогательные расчеты для определения средней гармонической
- •1. Понятие вариации и основные виды показателей вариации
- •Вспомогательная таблица для расчета показателей вариации
- •На основе исходных данных вначале подсчитываются средние величины, а затем находятся отклонения от средних. Рекомендуется в расчетах показателей вариации пользоваться формулой средней взвешенной.
- •2.Свойства средней арифметической и дисперсии
- •Свойства дисперсии
- •(Свойство минимальности).
- •3. Изучение структурных характеристик вариационного ряда
- •2. Показатели концентрации и дифференциации
- •3. Показатели структурных сдвигов
- •Лекция №7. Методология организации выборочных наблюдений5.
- •1.Задачи выборочного наблюдения и различные способы формирования выборки
- •Способы отбора единиц из генеральной совокупности
- •2. Понятие «ошибка выборки» и способы ее расчета
- •3. Расчет оптимальной численности выборки
- •Лекция №8. Методы и показатели оценки тесноты статистических взаимосвязей.
- •1.Понятие «статистическая взаимосвязь»
- •2. Классификация методов оценки тесноты статистических связей
- •3. Аналитические показатели оценки тесноты взаимосвязей между количественно измеримыми признаками
- •Вспомогательная таблица для расчета рангового коэффициента корреляции Спирмена
- •4.Способы оценки тесноты взаимосвязей между качественными признаками
- •Лекция №9. Статистическое изучение динамики социально -экономических процессов и явлений.
- •2. Аналитические показатели динамики
- •Аналитические показатели динамики
- •3. Сглаживание (выравнивание) динамических рядов: механическое и аналитическое сглаживание
- •Лекция №10. Построение уравнений тренда и уравнений парной линейной регрессии
- •1. Сущность метода наименьших квадратов
- •2. Построение уравнений регрессии
- •Расчет параметров парной линейной регрессии
- •3. Построение уравнений тренда
- •Вспомогательная таблица для расчета параметров уравнений линейного и квадратического тренда
- •4. Расчет корреляционного отношения на основе уравнения регрессии
- •Способы отбора факторных переменных.
- •Исходные данные для построения уравнений регрессии
- •После подсчета сумм в нижней строке таблицы, находим линейный коэффициент корреляции:
- •Матрица коэффициентов парной корреляции
- •Использование метода наименьших квадратов для построения нелинейных уравнений регрессии
- •Нелинейные относительно оцениваемых параметров
- •1. Понятие «статистический индекс»
- •2.Различные виды статистических индексов и способы их расчета
- •Различные виды агрегатных индексов
- •Вспомогательная таблица для расчета агрегатных индексов по формулам Ласпейреса и Пааше
- •3. Сущность индексного метода в статистике
- •Примеры решения задач индексным методом.
- •1. Понятие «прогноз» и виды прогнозов
- •2. Сущность статистических методов прогнозирования и требования к исходной статистической информации
- •3.Прогнозирование на основе уравнений тренда
- •1.Кластерный анализ
- •Дискриминантный анализ
- •3.Факторный анализ (метод главных компонент)
2. Классификация методов оценки тесноты статистических связей
Для выявления статистических связей и измерения степени их тесноты в статистике используются различные методы, основными из которых являются:
Метод параллельных рядов.
Метод таблиц сопряженности.
Расчет специальных аналитических показателей (или показателей корреляции7), оценивающих степень тесноты связи;
Построение уравнений регрессии, количественно выражающих статистическую взаимосвязь между двумя и более признаками, в виде уравнения некоторой математической функции8.
Метод параллельных рядов заключается в том, что параллельно выстраивается два ряда значений количественно измеримых признаков (показателей), причем первый (ряд значений признака x) из них выстраивается в порядке возрастания. Затем проверяется, будет ли соблюдаться тенденция к возрастанию соответствующих значений признака y во втором ряду. Если такая тенденция соблюдается, значит, между двумя признаками имеется статистическая взаимосвязь.
Таблица сопряженности – эта таблица, в которой по вертикали и по горизонтали выстроены различные значения двух признаков (x и y) в порядке возрастания. На пересечении строк и столбцов таблицы стоят числа, выражающие количество статистических единиц, одновременно обладающих соответствующими значениями признаков (x и y). Если ненулевые (т.е. не равные нулю) элементы таблицы сосредоточены вокруг ее главной диагонали, значит, между признаками имеется связь.
Таблицы сопряженности могут использоваться не только для оценки степени тесноты взаимосвязи между количественно измеримыми признаками, но и между качественными (альтернативными) признаками, которые условно принимают только два значения (0 и 1). Число 1 означает, что данная статистическая единица обладает этим признаком, а 0 – не обладает.
К специальным аналитическим показателям, измеряющим тесноту статистических взаимосвязей, относятся:
а) линейный коэффициент корреляции;
б) ранговый коэффициент корреляции Cпирмена;
в) корреляционное отношение и другие9.
Формулы для расчета перечисленных показателей приведены в таблице 8.1.
Все эти показатели выражены числами, абсолютная величина которых изменяется в пределах от 0 до 1. Чем ближе модуль данного числа к 1, тем связь считается более тесной. Линейный и ранговый коэффициенты корреляции могут принимать как положительные, так и отрицательные значения (положительная величина этих коэффициентов характеризует наличие прямой связи, а отрицательная – обратной). Корреляционное отношение не может быть отрицательным, так как выражено в виде арифметического корня некоторой величины.
Кроме того, существуют специальные коэффициенты (коэффициент ассоциации, контингенции и другие), рассчитываемые на основе таблиц сопряженности и измеряющие взаимосвязи между качественными признаками.
Формула для расчета рангового коэффициента корреляции Спирмена выводится из обычной формулы линейного коэффициента корреляции в предположении, что он рассчитывается не для значений признаков, а для соответствующих рангов.
Таблица 8.1
Аналитические показатели оценки тесноты взаимосвязей между количественными признаками и способы их расчета
Виды аналитических показателей
|
Формулы для их расчета |
Линейный коэффициент корреляции |
|
Ранговый коэффициент корреляции |
|
Корреляционное отношение |
|
Индекс детерминации |
|