12 Свойства определенного интеграла

1 Интеграл как линейный функционал (линейные свойства определенного интеграла). Если f(х) – интегрируемая функция, то С· f(х) – интегрируемая; Если f(х) и g(х) – интегрируемая, то f±g – также интегрируемая.

Другими словами, интегрируемые на [а,b] функции образуют линейное пространство. Определенный интеграл отображает элементы этого пространства (т.е. функции) на числа. Он есть числовая функция от функции, т.е. функционал.

I(cf)=c·I(f) Постоянный множитель подынтегральной функции можно вынести за знак интеграла.

1. I(f+g)=I(f)+I(g)

Это и есть 2 линейных свойства определенного интеграла.

2. Интеграл как аддитивная функция

3. Свойства интеграла, выражаемые неравенствами

1) При а<b, для ограниченных функций имеем

2) Если на [а, b] (а < b) имеем f(х)≥0, то

13 Теорема о среднем для интеграла от непрерывной функции

Для интегрируемой ограниченной функции на [а, b], удовлетворяющей условию m≤f(x)≤M, (причем m=inf, М=sup (f(x)), имеем Если взять μ, m≤ μ≤M, то

Это т.н. теорема о среднем.

Если f(x) непрерывна, m=min f(x), М=max f(x) на [а, b], то в качестве μ можно взять значение f(x) в некоторой точке ξ. Тогда (для непрерывной f(x)) Значение f(ξ)=

называют средним значением функции на [а, b].

14 Дифференцирование интеграла по верхнему пределу.

Пусть f(t) – непрерывная функция t при а≤t≤b Рассмотрим Ф(х)=

Покажем, что '(х)= f(х), т.е. что (х) является некоторой первообразной для f(х). Имеем Ф'(х)=

мы установили, что всякая непрерывная функция f(t) имеет первообразную,

которую можно взять в виде

Т.О.неопределенный интеграл от функции f(х) можно представить в виде , где С – произвольная постоянная

15 Формула Ньютона-Лейбница

В соответствии с предыдущим, F(а)=С. Тогда Пользуясь этим, можно записать Это центральная формула математического анализа, справедлива для любой непрерывной функции f(t) . Это формула Ньютона-Лейбница.

16 Замена переменной интегрирования.

Пусть f(х) – интегрируемая функция (Римана), и мы имеем дело вычислением ( причем а < b) Пусть х= φ(t) – непрерывно дифференцируемая монотонная функция на интервале [α, β] (α<β), причем φ(α)=а, φ(β)=b. Тогда в этих условиях Эта формула немедленно получается учетом того, что F(a)+

17 Формула интегрирования по частям Можно пользоваться формулой ибо

18 простая формула прямоугольников численного интегрмрования

Пусть вычисляется интеграл Если f(х)≈const на [а,b] , то можно приближенно взять Ошибка порядка . Это формула прямоугольников.

19 простая формула трапеции численного интегрирования

, ошибка порядка .

20 простая формула парабол(Симпсона) числ инт

Ошибка интегрирования порядка

21 по составной формуле прямоугольников имеем

где Δ=(b-а)/n, n-любое натуральное число.

22 По составной формуле трапеций (n-любое натуральное):

23 По составной формуле Симпсона (n-четное, n=2к)

24 Приложения определенного интеграла.

Длина линии, площадь плоских фигур и площади некоторых поверхностей, объем некоторых тел:

1. Площадь задача о площади криволинейной трапеции решается с помощью определенного интеграла. В предположении, что эта фигура ограничена сверху линией у= f(х) , имеем (при f(х) >0) Если линия задана параметрически у= φ(t), х= ψ(t),

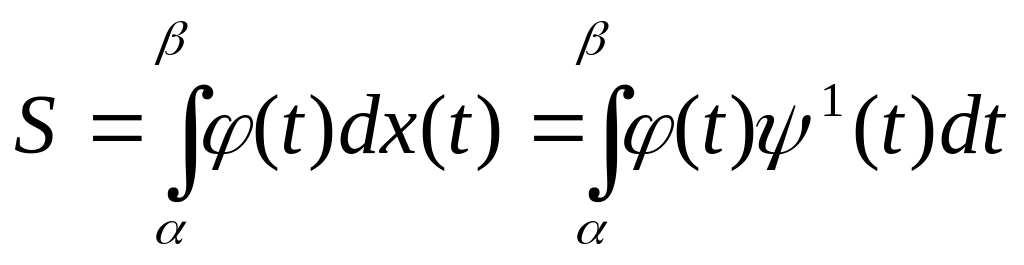
Площадь эллипса: х=аcost, y=bsint; 0<t<π/2; S=1/4 πаb·4= πab

Пусть, далее линия задана уравнением в полярных координатах:

х=r(φ) cos φ у= r(φ) sin φ r= r(φ) – задано

а требуется вычислить площадь сектора , . Тогда S≈1/2ΣΔφ_jr_j²=>

Пример: r=аφ. Это спираль Архимеда . Для нее

2.Объем тела. Пусть тело, для которого известны площади поперечных сечений, перпендикулярных некоторому направлению, вдоль которого затем задаем координатную ось Х. Итак S(х) – известны. Объем между сечениями в пределах от x=а до x=b:

Объем тела вращения y= , Длина дуги . Пусть линия задана уравнением у= f(х). (Δl_j)→0. .. 2 Если линия задана параметрически (x=φ(t), y=ψ(t)) , то получаем :

25 Эта сумма интегралов от непрерывных функций и есть интеграл от разрывной функции с точками разрыва первого рода c₁, c₂, …,c_k.