1 Первообразная функция

Функция F(х)называется первообразной функцией для функции f(х) на некотором интервале (а,b), если F^/(х)= f(х), или что тоже самоеdF=f(x) dx Теорема. Если функция F(х) является первообразной функцией для функции f(х), то F(х)+С также является первообразной для f(х), где С-произвольная постоянная величина.Это следует из того, что (F(х)+С)^/= F^/(х)= f(х).Убедимся, что любые две первообразные F(x) и (x) функции f(x) различаются на постоянное слагаемое. Имеем:

Тогда разность

что и требовалось.

Это выражение F(х)+С называется неопределенным интегралом от функции f(х), и обозначается символом . Итак, по определению .

Свойства неопределенного интеграла

1) символы d и взаимно сокращаются

2) Ибо есть первообразная для

3)

4)

2 Интегрирование по частям

Метод интегрирования по частям основан на известном дифференциальном равенстве где u и v –функции от аргумента x

Тогда откуда .

Это и есть формула интегрирования по частям. Замена переменной в неопределенном интеграле Предположим, что нам известен неопределенный интеграл

. Тогда будем иметь: , где w(x) – произвольная дифференцируемая функция от аргумента x.

3 Понятие о «не берущихся» интегралах.

Существуют «берущиеся» и «не берущиеся» интегралы.

Неопределенные интегралы вида , , , ,

, , , (p, k - некоторые постоянные величины), и некоторые другие не выражаются в виде конечной комбинации элементарных функций - они «не берущиеся».

4 Интегрирование дробно-рациональных выражений.

от дробно-рациональных функций вида . С этой целью прежде, чем говорить об , рассмотрим элементарные (в смысле интегрирования) простые дроби (дробные выражения)

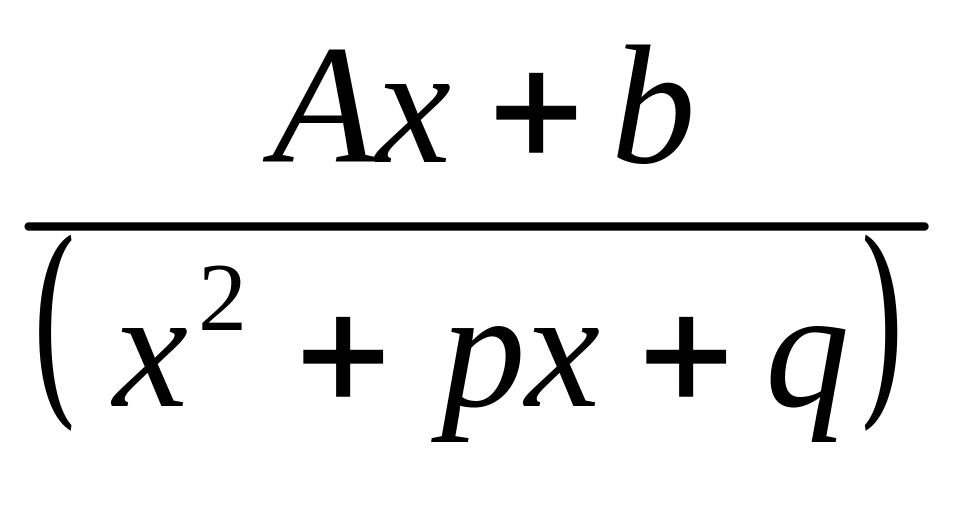1. 2. 3. 4.

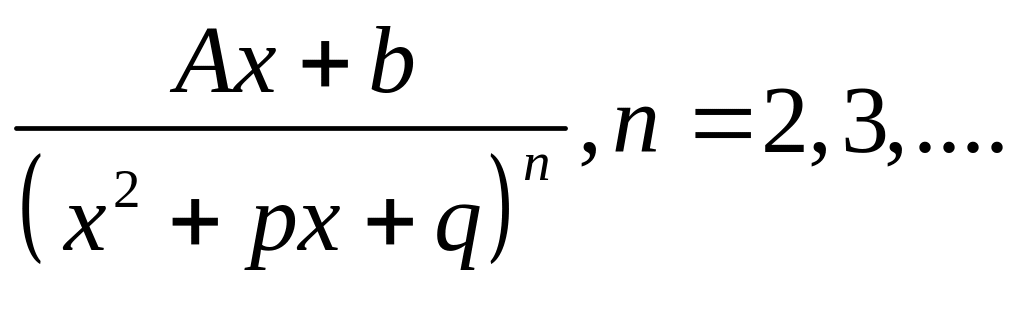
где А, a, b, р, q- вещественные числа, причем - трехчлен, не имеющий действительных корней, т.е. ;

3.

Еще прием для интегрирования таких дробных выражений:

; ; Тогда

5 Деление в ,,уголок’’

Разложение правильных дробей Р_m(х)/Q_n(x) на простые. Правильная дробь – это дробь вида Р_m(х)/Q_n(x) , n > m. Если , то делением « в уголок» можно представить в виде где R_k (x) – многочлен, а . Пусть Р_m(x)/Q_n(x)- правильная дробь. Разложим знаменатель на множители: Q_n ( причем k₁+k₂+…..+2m₁+…+2m_s=n) Берем многочлен ; тогда где A - постоянная, подлежащая определению, А=Соnst. Тогда

; однозначно находим A, поскольку . Повторяя процедуру, находим

далее повторяем процедуру относительно корня b, тогда

и т. д.Так можно перебрать все действительные корни.

7 Упрощение вида Пусть Покажем, что равенство P_m (x) – (Ax+B)Q_n-2r(x) = P_m-2(x)(x²+px+q) возможно. Для этого

A и B определяем так, чтобы левая часть делилась на x²+px+q. Обозначим остаток от деления Р_m(x) на x²+px+q чрез Мx+N, а Q_n-2r(x) на x²+px+q – через Zx+K. Тогда задача сводится к подбору А и В, чтобы делилось нацело на x²+px+q.

-АZx²+(M-ZB+Ak) x+N - BK= - AZ(x²+ ) пропорционально x²+px+q. Делим и здесь, определяем остаток и требуем, чтобы и этот остаток обратился в нуль. Получаем:

2 уравнения с двумя неизвестными A и B = ? остальные величины в этой системе известные. Можно видеть, что эта система уравнений разрешима относительно A и B.

прежде чем интегрировать правильную дробь P_m(x)/Q_n(x), ее надо представить в виде комбинации элементарных в смысле интегрирования дробей вида:

Коэффициенты A,…,С, D, …,М и т.д. удобно находить, решая систему алгебраических уравнений.