45. Аналитические свойства суммы степенных рядов:

1. Степенной ряд равномерно (правильно) сходится на любом замкнутом интервале [-b, b], находящемся внутри интервала сходимости (-R, R). Действительно, берем любое x₀, лежащее между b и R: . Тогда для любого ряд мажорируется числовым рядом , который сходится. Следовательно, и наш степенной ряд сходится равномерно по признаку Вейерштрасса.

2. Степенной ряд, составленный из производных имеет тот же радиус сходимости R, что и исходный ряд . Это свойство легко доказывается в случае существования предела . Тогда 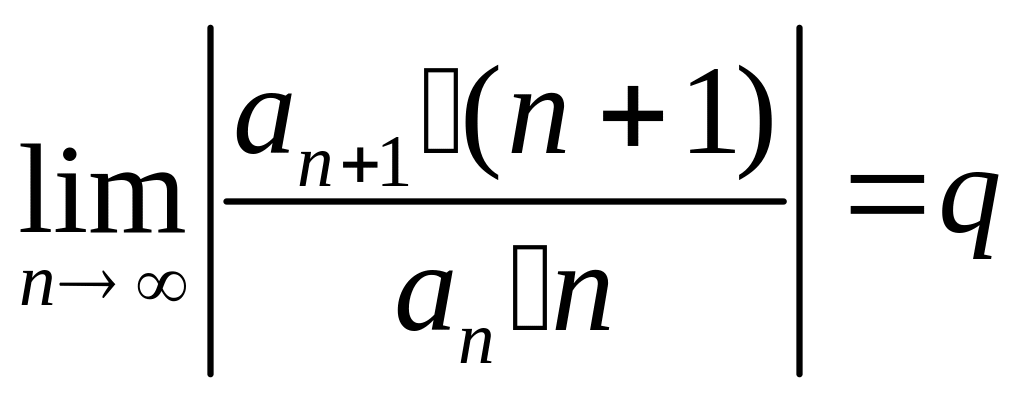что и требовалось.

Отсюда в частности следует, что все степенные ряды, получаемые почленным дифференцированием исходного ряда, имеют один и тот же радиус сходимости. Все эти ряды будут сходиться правильно на замкнутом отрезке, лежащем внутри интервала сходимости.

3. Сумма степенного ряда непрерывна в каждой точке x₀ интервала (-R, R) (ибо он сходится равномерно на отрезке [-x₀, x₀]). Рассмотрим пример ряда: =S(x). Функция S(x) разрывна только при x=1, но вне интервала сходимости она не является суммой ряда.

4. Степенные ряды можно почленно интегрировать в интервале сходимости (-R, R). Пусть a и b – точки, лежащие внутри (-R, R). Тогда будем иметь:

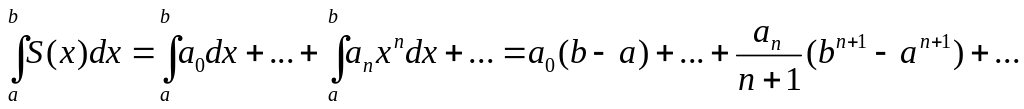
5. Степенные ряды можно почленно дифференцировать в любой точке интервала сходимости, причем будем иметь:

46.Выражение коэффициентов сходящегося степенного ряда через сумму ряда. Ряд Маклорена и ряд Тейлора.

47.Разложение произвольной функции в ряд Маклорена и в ряд Тейлора. Формулировка достаточных условий сходимости этих рядов к порождающей функции.

Разложение функций в степенные ряды .

Сумма S(x) степенного ряда в интервале сходимости будет непрерывной и бесконечное число раз дифференцируемой функцией. Часто бывает интересно узнать обратный вопрос: какая функция f(x) может быть суммой некоторого степенного ряда? Прежде всего, ясно, что такая функция должна быть бесконечное число раз дифференцируемой в интервале сходимости. Далее, если эта функция является суммой ряда ( т.е. если f(x)= ), сходящегося в некотором конечном интервале, то с помощью неоднократного дифференцирования левой и правой частей этого равенства и удовлетворения равенству в точке в точке x₀ убеждаемся, что должны выполняться следующие соотношения:

Откуда заключаем, что коэффициенты степенного ряда a_n следующим образом (как и в формуле Тейлора) выражаются через производные функции f(x):

Тогда:

Итак, если функцию f(x) можно разложить в степенной ряд с центром в точке x₀ , то этот ряд имеет вышенаписанный вид. Он оказывается рядом Тейлора, а коэффициенты

называются коэффициентами Тейлора для функции f(x) в точке x₀. Всякий сходящийся степенной ряд является рядом Тейлора для своей суммы. Следует обратить внимание на то, что если предположить, что функция f(x) имеет все производные в точке x₀, то это еще не означает, что ее можно разложить в степенной ряд. Такой ряд может даже расходиться на всей оси x (кроме точки x₀). Но если он и сходится, то необязательно к функции, его породившей.

Примеры: Пусть функция f(x ) такова, что ее производные известные: . Тогда ряд будет иметь вид:

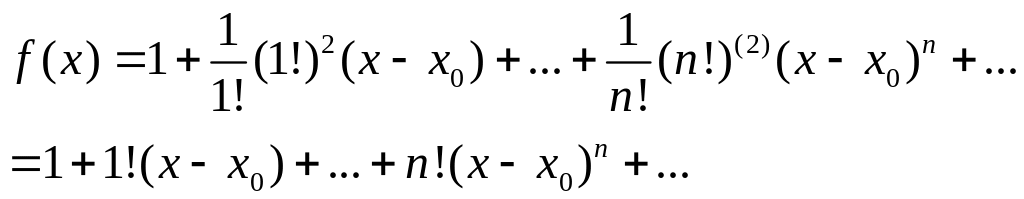
Этот ряд сходится только в точке x= x₀.Радиус сходимости этого ряда равен нулю.

Условия разложения функций в ряд Тейлора.

Теорема. Если в некотором интервале с центром в точке x₀ все производные ограничены одним и тем же числом (говорят тогда, что они ограничены по совокупности), то эта функция разлагается в ряд Тейлора.

Действительно, пусть производные обладают свойством ограниченности, т.е. пусть существует такое положительное число M>0, что для всех номеров n и для всех x из упомянутого выше интервала имеют место неравенства . Запишем формулу Тейлора для f(x):

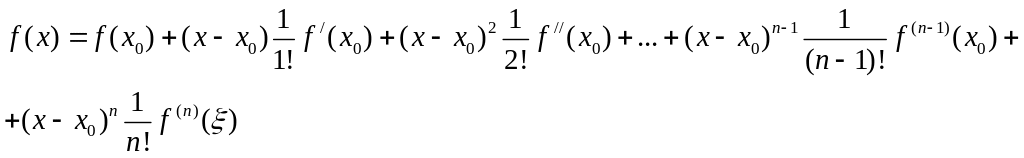
где  - некоторая точка, лежащая между точками x₀ и x. Так как f⁽ⁿ⁾(x) ограничена (для всех n), то .

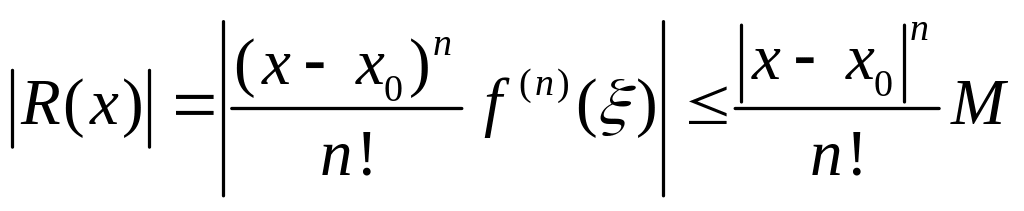Отношение стремится к нулю при любом заданном (зафиксированном) x и . В этом можно убедиться, формально рассмотрев ряд . По признаку Даламбера, он сходится, если