1. Непрерывность суммы равномерно сходящегося ряда.

Пусть ряд равномерно сходится в некоторой области D, причем его члены являются непрерывными в D функциями. Тогда и сумма ряд S(x) будет непрерывной функцией в области D.

Для доказательства обозначим S _n(x) частичную сумму ряда и пусть r_n(x) - остаток ряда. Имеем по определению: .

Тогда . Берем произвольную точку x₀ D . Рассмотрим и составим приращение суммы ряда в точке x₀ : . Далее, для модулей:

. Берем произвольное >0 . Подберем такое N, чтобы для всех n>N имели место неравенства: и

Тогда в D имеем: . Зафиксируем n и учтем при этом, что S_n(x) - непрерывная функция в точке x₀ . Тогда можно подобрать x , близкое к x₀ , чтобы . В итоге имеем неравенство , означающее в силу произвольности  непрерывность суммы ряда в произвольной точке x₀ области D, то есть и во всей области D.

2. Почленный переход к пределу.

Пусть в области D ряд сходится равномерно и его сумма равна S(x). Пусть существуют пределы , где a - точка области D. Тогда существует предел , причем (без доказательства).

3. Почленное интегрирование ряда .

Теорема. Если ряд из непрерывных функций u_n(x) сходится в области D : a  x  b равномерно, то сумму ряда S(x) можно интегрировать, причем

Таким образом, равномерно сходящийся ряд можно почленно интегрировать, причем проинтегрированный ряд будет сходиться. Имеем:

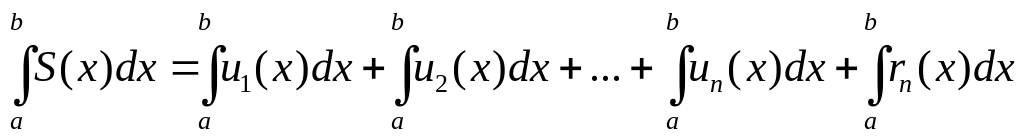
Берем >0. Докажем, что можно удовлетворить неравенству

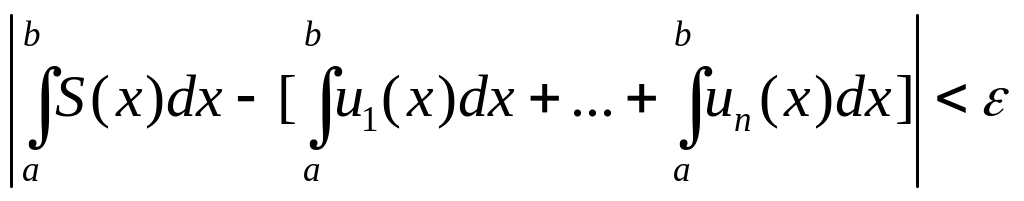
подбирая n большим. В силу равномерной сходимости ряда на отрезке a  x  b можно утверждать, что существует такое натуральное N , что при всех n >N , . Тогда: , что и требовалось.

Итак, для равномерно сходящегося ряда имеем: .

4. Теорема о дифференцировании ряда.

Пусть ряд сходится к S(x) равномерно в области D : [ a, b ] и пусть функции (все, при любом n) непрерывны в этой области. Тогда если ряд сходится равномерно в этой же области D , то его сумма равна . По-другому, имеет место равенство:

Действительно, если ряд равномерно сходится в области [ a, b ], то можно взять произвольную точку x из этого отрезка, и если в этой точке имеет место равенство , то прежде всего будем иметь в виду, что (x) непрерывна. Но тогда:

Следовательно, , что и требовалось доказать.

Аналогичные свойства верны и для правильно сходящихся рядов.

44. Степенные ряды. Теорема Абеля. Область сходимости степенного ряда и ее основные характеристики: центр сходимости и радиус сходимости степенного ряда.

Рассмотрим ряд, членами которого являются степенные функции от аргумента x:

Такой ряд называется степенным. В этом ряде действительные числа называются коэффициентами степенного ряда, величина x₀ –произвольно заданное действительное число, одно и то же для всех членов ряда, x - аргумент нашего функционального ряда. Величины и x₀ полностью задают степенной ряд. ьКраткая запись ряда: . В случае x₀ = 0 имеем ряд . Заметим, что при помощи преобразования x-x₀ = y можно свести задачу изучения ряда к изучению более простого ряда (в дальнейшем вместо y пишем x).

Для степенного ряда имеет место теорема Абеля:

Если степенной ряд сходится в некоторой точке x₀, отличной от нуля (x₀  0), то он сходится, причем абсолютно, и в любой точке x, удовлетворяющей условию . Докажем это.

Так как ряд сходится, то его общий член стремится к нулю при стремлении номера n к бесконечности. Следовательно, члены этого ряда ограничены как члены сходящейся (к нулю) последовательности . Это означает, что существует такое положительное число M >0, что для всех номеров n выполняются неравенства: . Тогда берем произвольное x ( ) и рассмотрим ряд: = = . Оценим абсолютную сходимость этого ряда : - сходится, ибо это геометрическая прогрессия со знаменателем .

Следствие. Если ряд расходится при x₀, то он расходится и при любом x, .

Область сходимости степенного ряда .

Из теоремы Абеля и следствия из нее вытекает, что если степенной ряд имеет отличные от нуля точки сходимости x₀ и точки расходимости x₁, то всякая точка сходимости лежит к началу координат не дальше, чем точка расходимости. При этом получается, что точки сходимости степенного ряда заполняют некоторый промежуток на числовой оси x с центром в начале координат. Этот промежуток можно характеризовать числом R таким, что в точках x, ряд сходится (причем абсолютно), а в точках x , - ряд расходится. В точках x=-R и x=R ряд может как сходиться, так и расходиться. Существование R можно объяснить так:

в точке x^*, лежащей между x₀ и x₁, будет либо сходимость, либо расходимость; так и перебираем точки отрезка [x₀,x₁], пока не исчерпаем весь этот отрезок.

Определение. Число R называется радиусом сходимости степенного ряда , если для всякого ряд сходится, а для всякого ряд расходится. Интервал (-R, R) называют интервалом сходимости, начало координат – центр интервала сходимости.

Разъяснение:

Для ряда центром интервала сходимости будет точка x₀ . Число R будет радиусом сходимости, если для ряд сходится, а для ряд расходится. Интервал сходимости этого ряда: -R+x₀ < x <R+x₀ . На концах интервала сходимости x=-R+x₀ и x= R+x₀ ряд может либо сходиться, либо расходиться.

Для отыскания радиуса сходимости , характеризующего область сходимости степенного ряда, можно поступать с рядом, как с числовым – применять к нему признаки Даламбера, Коши и другие.

Пусть, например, существует предел . Тогда находим ; ; . Если q=0, то вся действительная ось x является областью сходимости. Если q= , то ряд сходится только в точке x=0, а на всей оси x он расходится. Если же не существует (но, допустим, существует самая правая предельная точка (точка сгущения) числовой последовательности , то обозначив эту правую точку через находим, что заведомо ряд будет сходиться, если , т.е. если

Аналогично поступаем при применении признака Даламбера. Пусть существует 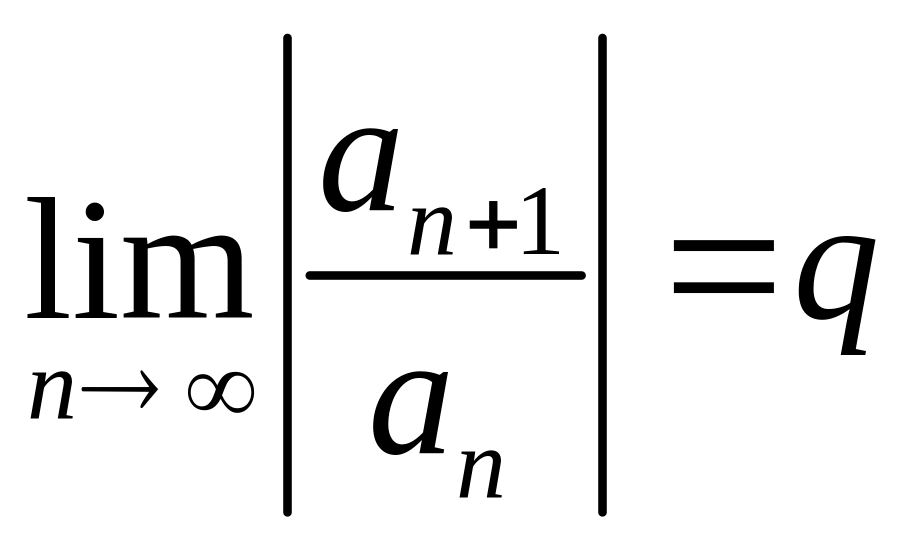. Тогда

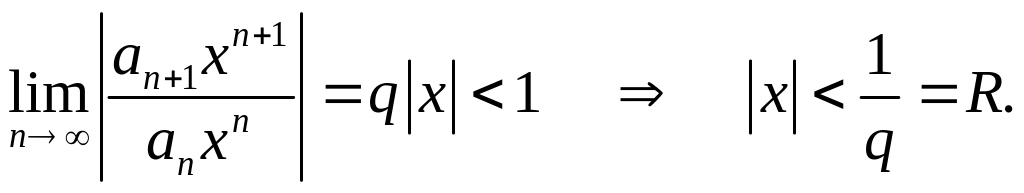Сходимость ряда на концах x=-R и x=R исследуется отдельно.