
- •35.Признак сравнения для рядов (в двух формах)
- •36.Признак Даламбера.
- •37. Признак Коши (радикальный). Интегральный признак Маклорена – Коши.
- •38. Сходимость знакопеременных рядов. Абсолютная и неабсолютная (условная) сходимость знакопеременного ряда.
- •39.Два свойства неабсолютно сходящихся рядов
- •40. Знакочередующиеся ряды. Признак Лейбница. Нахождение суммы ряда Лейбница с заранее заданной точностью.
- •Непрерывность суммы равномерно сходящегося ряда.
- •Почленное интегрирование ряда .
- •Теорема о дифференцировании ряда.
- •44. Степенные ряды. Теорема Абеля. Область сходимости степенного ряда и ее основные характеристики: центр сходимости и радиус сходимости степенного ряда.
- •45. Аналитические свойства суммы степенных рядов:
- •46.Выражение коэффициентов сходящегося степенного ряда через сумму ряда. Ряд Маклорена и ряд Тейлора.
- •47.Разложение произвольной функции в ряд Маклорена и в ряд Тейлора. Формулировка достаточных условий сходимости этих рядов к порождающей функции.
- •48.Разложение основных элементарных функций в ряд Маклорена (с указанием области сходимости).
- •49.Простейшие приложения рядов: приближенное нахождение определенных интегралов.
35.Признак сравнения для рядов (в двух формах)
Пусть имеем ряд A :
![]() ,
в котором все члены положительные:
,
в котором все члены положительные:
![]() (члены, равные нулю, можно выбросить из
ряда без ущерба для сходимости-расходимости
ряда).
(члены, равные нулю, можно выбросить из
ряда без ущерба для сходимости-расходимости
ряда).
Лемма. Если частичные суммы ряда
Sn=
a1 + a2+
… + an
с положительными членами ограничены
сверху (![]() ),
то ряд А сходится. Это связано с тем,
что последовательность частичных сумм
),
то ряд А сходится. Это связано с тем,
что последовательность частичных сумм
![]() строго
монотонна и ограничена сверху.
Следовательно, она имеет предел.
строго
монотонна и ограничена сверху.
Следовательно, она имеет предел.
Признак сравнения. Пусть даны два ряда:
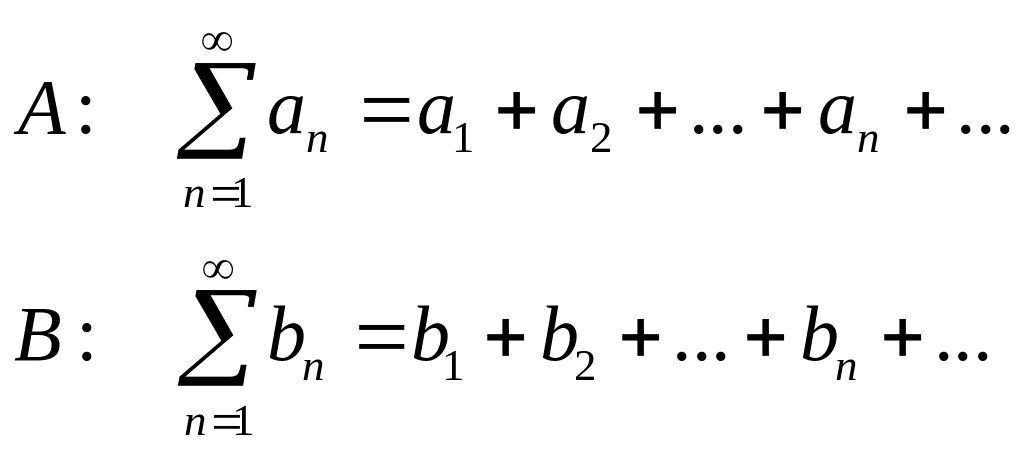
Пусть
![]() Тогда из сходимости ряда А следует
сходимость ряда В , из расходимости
ряда В следует расходимость ряда
А.
Тогда из сходимости ряда А следует
сходимость ряда В , из расходимости
ряда В следует расходимость ряда
А.
Действительно, если сходится ряд А, то есть если он имеет сумму, то частичные суммы ряда В будут ограничены сверху и будут строго монотонно возрастающими. По уже упоминавшемуся свойству монотонных ограниченных сверху последовательностей, частичные суммы ряда В будут иметь предел, ряд В также сходится.
Аналогично, если ряд В расходится, то это означает, что его частичные суммы неограниченны сверху. Но тогда и последовательность частичных сумм ряда А будет неограниченной сверху и предела иметь не будет, ряд А также расходится.
Если существует предел
![]() ,
то ряды А и В сходятся одновременно
(или расходятся одновременно).
,
то ряды А и В сходятся одновременно
(или расходятся одновременно).
Если же k=0, то из сходимости ряда В следует сходимость ряда А . При k= , из расходимости ряда В следует расходимость ряда А.
Аналогично, если ряд В расходится, то это означает, что его частичные суммы неограниченны сверху. Но тогда и последовательность частичных сумм ряда А будет неограниченной сверху и предела иметь не будет, ряд А также расходится.
36.Признак Даламбера.
Рассмотрим знакоположительный ряд
![]() .
Допустим, что имеется предел:
.
Допустим, что имеется предел:![]() Тогда при q<1 ряд А
сходится, а при q>1
ряд А расходится. Случай q=1
будет критическим, признак Даламбера
не дает ответа. Докажем сходимость
ряда А при q<1.
Поскольку q<1, то
существует q0,
удовлетворяющее неравенству q<q0<1.
Далее, так как
Тогда при q<1 ряд А
сходится, а при q>1
ряд А расходится. Случай q=1
будет критическим, признак Даламбера
не дает ответа. Докажем сходимость
ряда А при q<1.
Поскольку q<1, то
существует q0,
удовлетворяющее неравенству q<q0<1.
Далее, так как
![]() то существует N,
такое что для всех n
>N имеет место
неравенство:
то существует N,
такое что для всех n
>N имеет место
неравенство:
![]() ,
откуда
,
откуда
![]() .
Распишем эти неравенства подробнее:
.
Распишем эти неравенства подробнее:

Остаток
![]() ряда А сравниваем с остатком
геометрической прогрессии:
ряда А сравниваем с остатком
геометрической прогрессии:
![]() ,
который сходится, ибо знаменатель q0
этой прогрессии меньше единицы.
Следовательно, остаток RN
тоже сходится, ибо его члены меньше
членов сходящейся геометрической
прогрессии. А если остаток RN
сходится, то сходится и сам ряд А.
,
который сходится, ибо знаменатель q0
этой прогрессии меньше единицы.
Следовательно, остаток RN
тоже сходится, ибо его члены меньше
членов сходящейся геометрической
прогрессии. А если остаток RN
сходится, то сходится и сам ряд А.
Расходимость ряда А при q>
1 также следует из признака сравнения:
![]() что (n>N)
что (n>N)
![]() т.е. члены остатка
т.е. члены остатка
![]() и так далее – члены нашего ряда превосходят
члены расходящейся геометрической
прогрессии, ряд А также расходится.
и так далее – члены нашего ряда превосходят
члены расходящейся геометрической
прогрессии, ряд А также расходится.
37. Признак Коши (радикальный). Интегральный признак Маклорена – Коши.
Признак Коши. Рассмотрим
ряд A :
с положительными членами. Пусть существует
![]() Тогда если q <1,
то ряд сходится, если q>1
то ряд расходится. При q=1
признак Коши ответа не дает.
Тогда если q <1,
то ряд сходится, если q>1
то ряд расходится. При q=1
признак Коши ответа не дает.
Для доказательства рассмотрим
прогрессию
![]() , где
, где
![]() .
Тогда ясно, что эта прогрессия сходится,
ибо
.
Тогда ясно, что эта прогрессия сходится,
ибо
![]() Но:
Но:
![]() при n>N.
Следовательно
при n>N.
Следовательно
![]() ;
Из сравнения с написанной сходящейся
прогрессией следует сходимость нашего
ряда.
;
Из сравнения с написанной сходящейся
прогрессией следует сходимость нашего
ряда.
Расходимость
при
![]() следует из того, что например
следует из того, что например
![]() не стремится к нулю.
не стремится к нулю.
Пример:
![]() .
Сходится ли этот ряд? Имеем
.
Сходится ли этот ряд? Имеем
![]() при
при
![]() .
Ряд сходится при всех x.
.
Ряд сходится при всех x.
Интегральный признак сходимости. (Маклорена – Коши).
Пусть дан ряд
,
члены которого являются значениями
непрерывной монотонно убывающей функции
![]() при целочисленных значениях аргументов,
т.е.
при целочисленных значениях аргументов,
т.е.
![]() .
Тогда ряд сходится или расходится
одновременно с несобственным интегралом:
.
Тогда ряд сходится или расходится
одновременно с несобственным интегралом:
 .
.
Доказательство. Пусть интеграл сходится и пусть =S0. Но тогда из геометрических соображений видно, что
 или:
или:
 .
Перепишем это неравенство:
.
Перепишем это неравенство:
![]() ,
,
![]() - последовательность частичных сумм
- последовательность частичных сумм
![]() ограничена сверху. Поскольку она
монотонно возрастает, то имеет предел
– ряд сходится.
ограничена сверху. Поскольку она
монотонно возрастает, то имеет предел
– ряд сходится.
Пусть теперь интеграл
расходится. Тогда
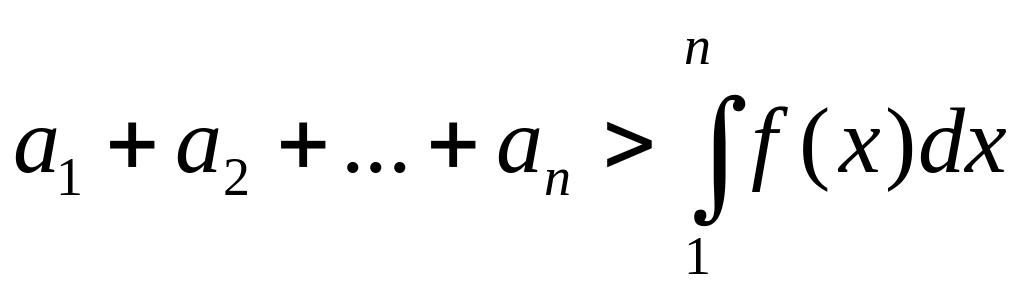 .
С возрастанием номера n
правая часть этого неравенства
неограниченно растет, ряд расходится.
.
С возрастанием номера n
правая часть этого неравенства
неограниченно растет, ряд расходится.
Пример. Рассмотрим достаточно общий
ряд
![]() ,
где s - произвольная
постоянная величина. При s
= 1 ряд превращается в гармонический
,
где s - произвольная
постоянная величина. При s
= 1 ряд превращается в гармонический
![]() и расходится. Пусть теперь s>1.
Применим интегральный признак.
Полагаем
и расходится. Пусть теперь s>1.
Применим интегральный признак.
Полагаем![]() ,
находим :
,
находим : .
Интеграл сходится, и ряд также сходится.
При s<1 имеем:
.
Интеграл сходится, и ряд также сходится.
При s<1 имеем:
 .
Интеграл расходится – ряд также
расходится. Итак, ряд сходится при s
>1 и расходится при s1.
.
Интеграл расходится – ряд также
расходится. Итак, ряд сходится при s
>1 и расходится при s1.
