18. Виды сбалансированных деревьев, достоинства и недостатки.

Виды деревьев	Достоинства	Недостатки
Дерево поиска	Простота операции поиска, вставки, удаления	Не сбалансированное
Идеально сбалансированное дерево	Наименьшее возможное время поиска = O(log N)	Нет операции вставки и удаления
АВЛ	Поиск, вставка, удаление за O(log N)	Необходимость выполнять операции балансировки
Красно-черные ( = СДБ)	См. СДБ	См. СДБ
Б-дерево	Возможность создания очень больших разветвленных деревьев	Требуются обращения ко вторичной памяти
ДБ-деревья		Хуже, чем СДБ
Дерево оптимального поиска	Оптимальный поиск при различных вероятностях ключей (чем больше вероятность, тем ближе к корню)	Нет операций вставки и удаления; Сложность построения O( )
Splay-дерево	Сбалансированно Время операций O(log N)	Могут вырождаться в линеный список

19. Дерево оптимального поиска

Бывают случаи, когда информация о вероятности появления ключа известна. В таких ситуациях характерно постоянство ключей, то есть ключи не добавляются, не удаляются, и сохраняется структура дерева. И для сокращения времени необходимо использование таких деревьев, в которых самые часто встречающиеся вершины находились бы ближе к корню дерева.

1. Будем рассматривать дерево с псевдовершинами. Т. е. обнаружение того факта, что некий ключ k не является ключом в дереве поиска, можно рассматривать,как обращение к псевдовершине (псевдоузлу), вставленной между ближайшими меньшим и большим ключами.

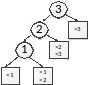
2. Вместо вероятности 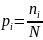, будем рассматривать:

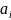– число поисков вершины ;

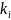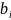– число поисков псевдовершины , .

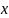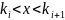(Если поделить и на N, то получится та же самая вероятность)

3. Длина средневзвешенного пути:

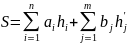
n – количество вершин,

m – количество псевдовершин,

ai, bi – вершина и псевдовершина соответственно,

hi, hj – уровень вершины, псевдовершины соответственно.

Свойство:

Любое поддерево дерева оптимального поиска является оптимальным.

Т. е. если дерево оптимального поиска разделим пополам относительно вершины, то левои и правое поддерево по основному свойству будут также оптимыльными.

Тогда длина средневзвешенного пути для левого поддерева:

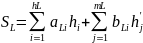
Длина средневзвешенного пути для правого поддерева

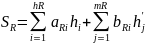
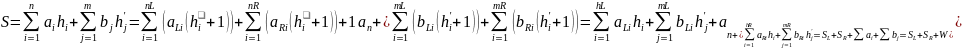
W – вес дерева оптимального поиска – количество всех возможных поисков.

Построение дерева:

1. Построение таблицы весов, 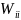– вес дерева 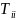(дерево с ключами ;

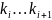2. Достраиваем таблицу, ;

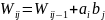3. Таблица путей, ;

4. .

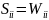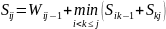Сложность .
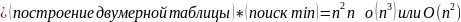
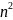