14. Дерево поиска. Основные операции, вычисление средней длины пути.

Дерево поиска – все вершины в правом поддереве > x (вершина), все вершины в левом поддереве < x.

В дереве поиска можно найти любой ключ, стартуя с корня и спускаясь в левое или правое поддерево в зависимости только от ключа в текущем узле. Если дерево идеально сбалансировано, то поиск среди n элементов можно выполнить за О(logn). Этим деревья поиска выгодно отличаются от линейных списков.

Операции:

Обход дерева

О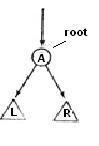 бход дерева можно совершать тремя способами:

1. A,L,R(префиксный обход)

2. L,A,R (инфиксный обход)

3. L,R,A (постфиксный обход)

(подробно см. пункт 12)

Поиск вершины

Использование двоичного дерева поиска позволит найти искомую вершину за О(logn), причем высота дерева составляет log₂n.

Добавление

Данная операция соотносится с операцией поиска и они объединяются в одну – поиска-включения. При этом минимальной время – O(log₂n), максимальное - O(n). Аналогом по быстродействию является быстрая сортировка и поиск медианы в ней.

Если дерево пусто, заменить его на дерево с одним корневым узлом ((K,V), null, null) и остановиться.

Иначе сравнить K с ключом корневого узла X.

• Если K>=X, рекурсивно добавить (K,V) в правое поддерево Т.

• Если K<X, рекурсивно добавить (K,V) в левое поддерево Т.

Удаление

Если дерево T пусто, остановиться;

В остальном различают 3 случая:

• Отсутствует компонента с ключом, равным х.

• У компоненты с ключом х не более 1 потомка.

• У компоненты с ключом х 2 потомка. В этой ситуации элемент должен быть заменен либо на самый правый элемент левого поддерева, либо на самый левый элемент правого поддерева.

Вычисление средней длины пути в дереве поиска:

П

i

усть вершины пронумерованы от 1 до n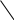

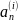– средняя длина пути

L

R

i-1 вершина

n-i вершин

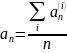
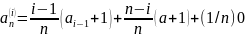– левое поддерево, правое поддерево, корень

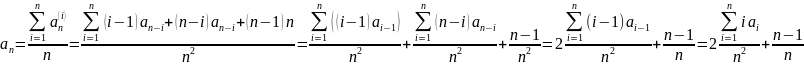
а) Преобразуем

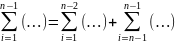
б) сумму считаем до (n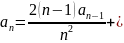-1)

(1)

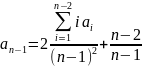(2) умнож. на

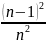
Подставляем (2) в (1)

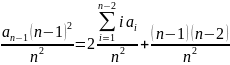
Тогда

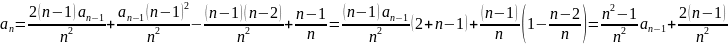
По индукции можно доказать следующее

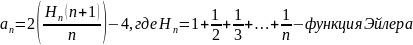
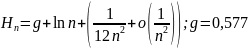- при больших n последнее слагаемое опускаем

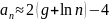
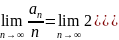
В среднем случае длина пути случайного дерева отличается от длины пути в идеально сбалансированном на 38%, в большинстве случаев это не критично, но если задача связана с максимально быстрым поиском, то нужно строить идеально сбалансированное.

15. АВЛ-СБАЛАНСИРОВАННЫЕ ДЕРЕВЬЯ. ОПЕРАЦИИ, СЛОЖНОСТЬ.

АВЛ-сбалансированное дерево – двоичное дерево, сбалансированное по высоте, в котором высоты поддеревьев каждой из вершин отличаются не больше, чем на 1.

Пример АВЛ – деревья Фибоначчи, где каждое следующее строится на основе двух предыдущих.

Формула, определяющая количество вершин для дерева Ф. n-ого порядка – рекурсивная:

.

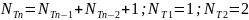За время О(log n) можно сделать операции включения вершины с данным ключом, исключения, найти вершину с данным ключом.

АВЛ никогда не будет выше ИДБ чем на 45%:

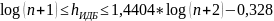
Операция вставки:

Проход по пути поиска, включение и проверка на нарушение баланса, балансировка.

Пусть новый узел вставляется в L, увеличивая его высоту на 1, тогда имеют место 3 случая:

1. hl=hr: после вставки высота становится неравной, но критерий балансировки не нарушается

2. hl<hr : высоты становятся равными, баланс только улучшается

3. hl>hr : критерий балансировки нарушается, и дерево требуется перестроить

Рассматриваем 4 случая (случай 3 и 4 – зеркальные отображения случаев 1 и 2 соответственно):

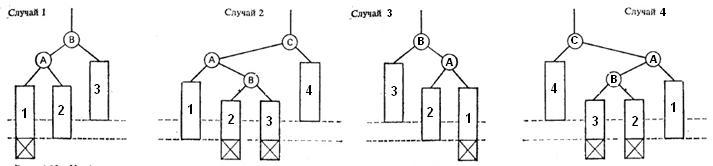
Одигарный поворот(LL) Двойной поворот(LR) (RR) (RL)

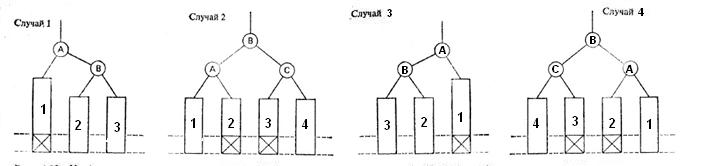
Алгоритм определения типа поворота (при добавлении в левое поддерево, с правым наоборот):

1. Находим ближайшую к низу вершину, которая является разбалансированной.

2. Рассмотрим ее левое поддерево. Если левое поддерево этого поддерева выше правого, то случай 1, иначе – случай 2.

3. Расставляем буквы и цифры, осуществляем поворот согласно схемам.

Сложность операции балансировки предполагает, что АВЛ используют, когда поиск проиcходит чаще, чем включение, иначе следует брать СДБ.

Операция изменения ссылок не зависит от размера дерева и составляет O(1), операция просмотра сверху вниз O(log n)итого – O(1)+2 O(log n).

Пример:

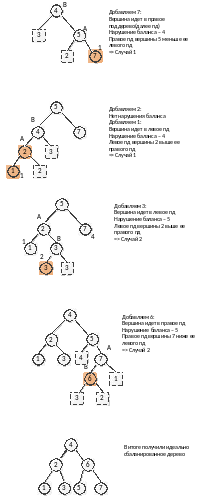
Операция удаления – как в дереве поиска + балансировка

Операции вставки и удаления – происходят как в дереве поиска, при этом после каждого действия требуется проверка на нарушение баланса и, при необходимости, выполнение балансировки по указанной схеме.

В среднем случае: на 2 включения 1 балансировка. А при удалении поворот в 1 случае из 5.

Процедура удаления из сбалансированного дерева строится на основе алгоритма удаления из обычного дерева. Простые случаи – концевые узлы и узлы с единственным потомком.

В худшем случае удаление проводится за O(logn).

16. Б-ДЕРЕВЬЯ. ОПЕРАЦИИ, СЛОЖНОСТЬ.

Б-деревья - сбалансированные сильно ветвящиеся деревья, удобные для хранения информации на дисках. Характерным для Б-деревьев является их малая высота h. Представление информации во внешней памяти в виде Б-дерева стало стандартным способом в системах баз данных.

В Б-дереве узел может иметь много сыновей, на практике до тысячи. Количество сыновей (максимальное) определяет степень Б-дерева.

Если задана некоторая верхняя граница числа потомков, то модно представить их как компоненты некоторого массива в записи, представляющей любую вершину. Если число потомков у разных вершин варьируется, то такое представление может привести к плохому использованию доступной памяти. В этом случае проще представлять потомков в виде линейного списка со ссылками от предка на самого младшего или старшего потомка (но операции в этом случае буду сложнее).

Применение сильно ветвящихся деревьев - поиск в больших объемах данных, которые не помещаются в оперативную память.

Б-деревья делят на страницы. Мы получаем структуры, которые помещаются в одно окно, тогда поиск идет не вниз, а вширь – вероятность найти объект выше.

Б-дерево порядка n обладает следующими свойствами:

• Каждая страница содержит не более 2n элементов.

• Каждая страница, кроме корневой, содержит не менее nэлементов.

• Каждая страница представляет собой либо лист (не имеет потомков), либо имеет m+1 потомков, где m-число ключей на данной странице.

• Все страницы-листья находятся на одном уровне

Б

Стр 1

-дереьвья порядка 2:

10

20

30

m = 3,

(m+1) ключей

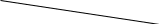
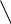
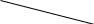
8

9

11

15

17

21

29

31

35

38

40

Операции:

Поиск ключа: Читаем первую страницу, ищем ключ, если не находим, то переходим по ссылке между 2 наиболее близкими к искомому ключами.

Например: ищем 15 – переходим по ссылке межу 10 и 20 и т.д.

Вставка: сначала с помощью поиска находим место. Если на станице m<2n, то вставляем. Иначе создаем новую страницу-соседа, распределяем 2n ключей между ними, но 1 ключ (по значению средний) уходит наверх на родительскую страницу.

Удаление: Если m>n, то удаляем. Иначе берем элементы с соседней страницы (если не хватает, сливаем 2 страницы вместе).

Для дерева из N элементов для выполнения операций потребуется не более k=log_nNрекурсивных вызовов (обращений к страницам), коэффициент использования памяти = 50%, т. к. страницы всегда заполнены минимум на половину

17. ДБ- И СДБ- ДЕРЕВЬЯ. ОПЕРАЦИИ, СЛОЖНОСТЬ.

ДБ-дерево.

Максимальное количество ключей на странице – 2, ссылки могут быть не только вертикальными, но и горизонтальными. Реализация (представление в виде массива не удобно и не эффективно, поэтому используют линейные списки):

struct DBTree {

Tdata data;

struct DBTree *left;

struct DBTree *right;

bool h; //чтобы обозначить, по горизонтали или по вертикали направлена правая ветвь

}

Максимальная длина пути = 2log N, при включении характерен рост к корню.

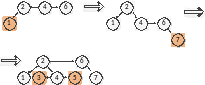
Схемы включения в ДБ-дерево:

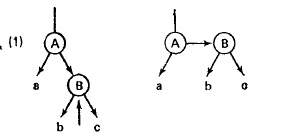
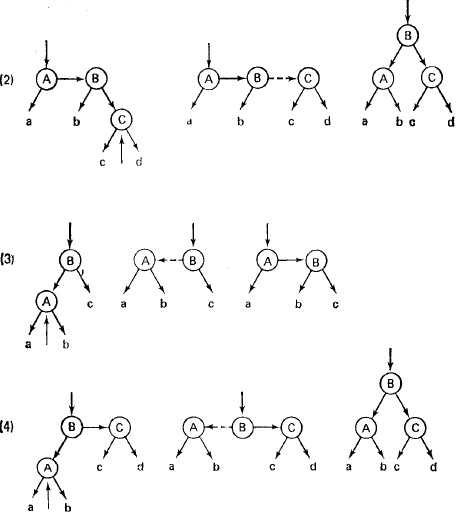
Пример:

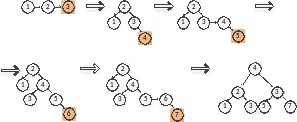
СДБ-дерево.

Возможность делать ссылки в обе стороны, т. е. иметь левого и правого брата.

Свойства:

• Каждая вершина имеет 1 ключ и не более 2 ссылок на поддеревья.

• Ссылки могут быть вертикальными и горизонтальными. Нет ни одного пути поиска с 2 подряд идущими ссылками.

• Все листья находятся на одном уровне.

Длина самого протяженного пути поиска не более, чем вдвое, превышает высоту дерева log N,

т. е. путь поиска <= 2 log N.

СДБ удобно для вставки.

Реализация:

struct SDBTree {

Tdatadata;

struct SDBTree *left;

struct SDBTree *right;

boo lhr;

boo lhl;

}

Операция вставки:

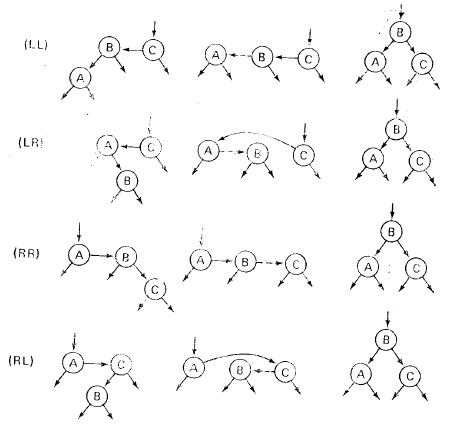
Пример:

Операция поиска занимает 2 log N – на одном уровне можем сделать <= 2 действий.