1.7 Идеально-газовая шкала температур.

На основании сказанного, можно сделать вывод: для измерения температуры необходима такая термометрическая величина, изменение которой с температурой было бы независимо (или слабо зависимо) от химической природы вещества.

Почти такой термометрической величиной характеризуется газообразное состояние вещества, подчиняющееся уравнению Клапейрона-Менделеева:

(1.7.1)

Как видно из (1.7.1), давление газа при постоянном объёме и объём газа при постоянном давлении могут быть взяты в качестве термометрической величины, однако и здесь возникают те же трудности, так как реальные газы лишь приближённо могут рассматриваться как идеальные, т.е. удовлетворяющие уравнению (1.7.1).

Поэтому для устранения снова возникающей неоднозначности принято все термометры градуировать по эталонному газовому термометру с термометрическим телом Не (гелий) и термометрической величиной Р (давление газа) при постоянном объёме. Этот выбор обосновывают тем, что:

1. Гелий, после водорода, в наименьшей степени отклоняется от законов идеального газа (отклонения эти для воздуха, азота, углекислого газа и т.п., больше, чем для гелия). Исключение водорода связано с тем, что при высоких температурах он начинает химически действовать на материал сосуда (как правило стекло), в котором он находится.

2. Измерение давления газа при постоянном объёме производится с большей точностью, чем измерение объёма при постоянном давлении.

Однако и здесь возникают трудности: в области высоких температур применение эталонного гелиевого термометра ограничивается практическими осложнениями, а именно: гелий проникает через стенки сосуда, в котором он находится, при этом уменьшается число N молекул гелия в сосуде. В этих условиях гелий заменяют на азот. При низких температурах становятся заметными отступления от простого закона (1.7.1). Ввиду этого газовый термометр используют в качестве эталонного только для такого интервала температур, где с высокой степенью точности выполняется закон (1.7.1).

Таким образом, в идеально-газовой шкале температур в качестве термометрического тела выбирают газообразный гелий (азот), а термометрической величиной - его давление при постоянном объёме. Температуру в этой шкале обозначают буквой Т, а термометрическую величину х - буквой Р. Зависимость между ними выбирают линейной, вида (1.6.1) с b = 0, т. е.

(1.7.2).

Как видно из (1.7.2), температура в этой шкале равна нулю, когда давление газа Р = 0. Шкала, а также температура, измеренная в этой шкале, называется абсолютными, если в нуле температурной шкалы термометрическая величина обращается в нуль.

В абсолютной идеально-газовой шкале так же, как и в шкале Цельсия, разность температур между двумя реперными точками (температурой Т₁ плавления льда и температурой Т₂ кипения воды при нормальном атмосферном давлении) принимается равной 100, т.е. один градус в шкале Цельсия равен одному градусу в абсолютной шкале по определению. Таким образом, в абсолютной шкале

Т₂ –Т₁ = 100 (1.7.3).

Второе уравнение для определения значений температур в реперных точках абсолютной шкалы находится измерением давлений Р₁ и Р₂ соответствующих температурам Т₁ и Т₂ в реперных точках. Эти измерения дают

(1.7.4).

Решая уравнения (1.7.3). – (1.7.4), находим

Т₁=273,15К, Т₂=373,15К

Очевидно, любая температура Т в абсолютной шкале определяется по формуле (1.6.6).

(1.7.5).

Разделим обе части выражения (1.7.5) на T₁, получим

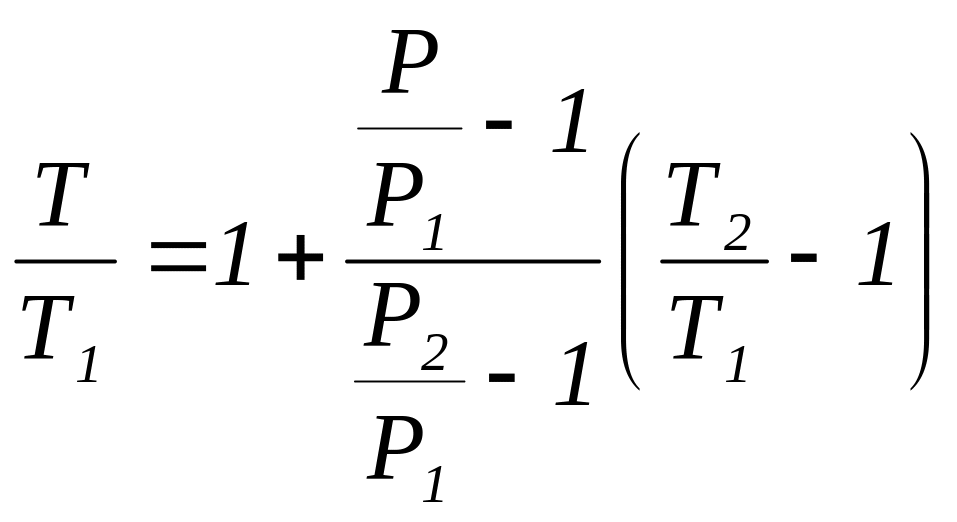(1.7.6)

Подставив (1.7.4) в (1.7.6), находим

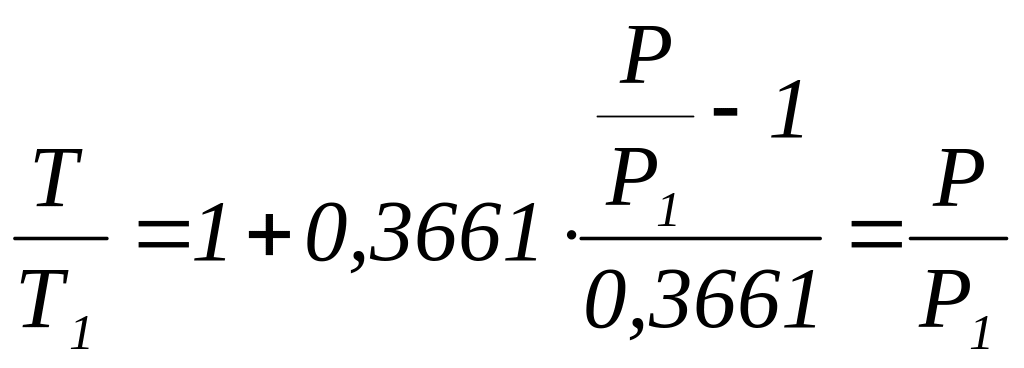(1.7.7)

или

, (1.7.8)

где Р₁ - давление в газовом термометре, находящемся в тающем льду. Чтобы при помощи газового термометра измерить температуру тела, необходимо это тело привести в тепловой контакт с газовым термометром и измерить манометром давление газа в нём. Тогда температура Т вычисляется по формуле (1.7.8).

Ввиду того, что так называемая тройная точка воды (одновременное сосуществование в равновесии трёх фаз воды твёрдой, жидкой и газообразной) значительно лучше воспроизводится на опыте, чем точки плавления льда и кипения воды, в 1954 году по международному соглашению абсолютная шкала или шкала Кельвина строится по одной реперной точке - тройной точке воды температуре которой приписываются точно Т_тр.= 273,16К (или 0,01С)

Тогда любая температура Т, измеряемая газовым термометром определяется по формуле, аналогичной (1.7.8):

(1.7.9)

Указанный выше выбор численного значения температуры тройной точки воды сделан для того, чтобы промежуток между точками плавления льда и кипения воды с максимально возможной точностью составлял 100 К. Тем самым устанавливается преемственность температурной шкалы Кельвина с абсолютной шкалой, определяемой двумя реперными точками. Измерения показали, что температуры точек плавления льда и кипения воды в шкале, Кельвина с одной реперной точкой равны приблизительно 273,15К и 373,15К. Единица температуры в этой шкале - Кельвин - 1/273,16 температурного интервала между тройной точкой воды и точкой абсолютного нуля температуры.

И, наконец, для шкал Кельвина и Цельсия на основании выражений (1.6.6) и (1.6.8)

(1.7.10)

(1.7.11)

Вычитая из (1.7.10) выражение (1.7.11), получим связь между шкалами Кельвина и Цельсия

Т,К = tС+273,15 (1.7.12)