10.Ознаки порівняння додатніх числових рядів.Приклади.

О-я:Якщо n а_n. - наз-ся знакододатній.

Заув-я:

Звластивості 1 випливає що дослідження знаковідьємного ряду рівносильно досл-ню рівносильного знакододатнього ряду.

Теорема1(ознаки порівняння)

Якщо n викон-ся нер-ть 0 а_n b_n (1) то із збіжності ряду (2) випливає збіжність (3) ,а розбіжності 3 випливає розб-ть 2.

Дов-ня: Нехай ряд 2 збігається , S_n= , і _n= - частинні суми рядів 3 і 2 т.к 2 збіг-ся то

lim_n _n =.Таким чином {S_n} обмежена зверху числом  крім того ця посл-ть не спадна.

За т-ю про існування границі обмеженої неспадної посл-ті одержимо що S=lim_n S_n тобто 3 збігається.

Нехай тепер ряд 3 розбіжний. Якщо ми припустимо що 2 збіжний то за доведеним 3 повинен бути збіжним, а це суперечить умові.

Ознаки порівняння можна застосовувати і тоді коли нер-ть 1 викон-я не для всіх n, а починаючи з деякого номера N. Оскільки за 3 на збіжність ряду не впливає приєднання скінченої кількості чисел.

Застосовуючи ознаки пор-х треба знати які ряди збіжні , а які розбіжні.

Т-ма2(причинна ознака порівняння)

Якщо задані 2 додатні числові ряда (4) , (5) існує границя lim_n а_n/b_n=e де 0<l<+, то ряди 4 5 збігаються або розбігаються одночасно тобто мають однакову поведінку.

Дов-ня: Нехай lim_n а_n/b_n=l тоді >0 існує N():n>N викон-ся нер-ть а_n/b_n -l<

(l-) b_n а_n (l+) b_n(6). Якщо 4 збіжний то з лівої частини 6 і Теор-и1 випливаєщо ряд також збіжний з властивості 1 числових рядів що тоді і також збіжний. Нехай 4 розбіжний тоді з правої частини 6 випливає що розбіжний тому за вл-ю 1 розб-й.

Наслідки:

1)Якщо аn екв-но bn, lim_n а_n/b_n=l то 4 5 або одночасно збіг-ся або розбіг-ся.

11. Знакоочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.

Знакопочередним називається такий числовий ряд знаки членів якого строго чергуються тобто ряд два довільні сусідні члени якого мають різні знаки: а₁-а₂+а₃-...+(-1)^n-1a_n+…= (1) де a_n0, n>N.

Теорема 1 (ознака Лейбніца): Ряд (1) збіжний якщо а_n > а_n+1, n>N (2) і lim_n а_n=0 (3).

Доведення: Розглянемо частинну сумму ряду (1) з парним числом членів S_2n=а₁-а₂+а₃-a₄+...+a_2n-1-a_2n= (а₁-а₂)+(а₃-a₄)+...+(a_2n-1-a_2n). З (2) випливає, що кожна різниця в дужках додатна, а тому S_2n0, n>N. Послідовність {S_2n} крім того монотонно зростає. Покажемо, що ця послідовність обмежена зверху, дійсно S_2n=a₁-[(а₂-а₃)+(а₄-a₅)+...+(a_2n-2-a_2n-1)+a_2n]  а₁. Таким чином посл-ть {S_2n}, як обмежена зверху монотонна посл-ть має границю. Позначимо її через: lim_n S_2n = S_.

Розглянемо тепер посл-ть частинних сумм з непарним числом членів S_2n+1= S_2n+а_2n+1.

Властивість (3): lim_n S_2n+1 = lim_n S_2n+ lim_n а_2n+1 = S+0=S . Таким чином lim_n S_2n+1 = lim_n S_2n = S це і означає, що ряд(1) збіжний.

Приклад: Дослідити на збіжність ряд . Даний ряд є знакопочереднім, для нього а_n=1/n, а_n+1=1/(n+1), lim_n а_n= lim_n 1/n=0 тому за теоремою 1 даний ряд збігається.

О-я: Ряд називається знакозмінним якщо серед його елементів є як додатні так і від’ємні числа.

З-я1: В даному означенні розглядається випадок коли числовий ряд містить нескінченну кількість додатніх членів і нескінченну кількість від’ємних членів. Зрозуміло, що розглянутий знакопочередній ряд є частинним випадком знакозмінного.

Нехай а₁+а₂+а₃+a₄+...+a_n+...= - знакозмінний ряд. Розглянемо ряд кладений із модулів його членів , справедлива теорема:

Теорема 2: Якщо збігається ряд , то збігається ряд .

Доведення: Позначимо через | a_n|+ a_n =2p_n, | a_n|- a_n =2q_n. Зрозуміло, що 0 2p_n |a_n |; 0 2q_n |a_n |. Оскільки ряд з модулів |a_n | збігається, то за ознакою порівняння: і також збіжні, але a_n = p_n - q_n. Тоді ряд = = - . За властивістю 2 числових рядів питання 14.

Приклад: Дослідити на збіжність ряд . Даний ряд є знакопочереднім, розглянемо ряд з модулів його членів: , оскільки |sin n|/n³1/n³, а ряд збігається (узагальнений гармонічний ряд з показником степені =31), то за означенням порівняння: |sin n|/n³ збіжний, тому за теоремою 2 збіжним буде ряд sin n/n³.

Зауваження: Теорема 2 дає лише достатню умову збіжності знакозмінного ряду тому, що твердження обернене до теореми 2 не виконується. Оскільки існують ряди, які є збіжними, а ряди побудовані з модулів їх членів розбігаються. Приклад: збігається, але ряд складений з модулів його членів розбіжний (гармонічний ряд).

О-ня 1: Ряд називається абсолютно збіжним якщо збігається ряд .

О-ня 2: Якщо ряд збігається, а ряд розбігається, то ряд називається умовно збіжним рядом.

У прикладах ряд збігається абсолютно, а ряд збігається умовно.

12.Функціональні ряди поняття рівномірной збыжн. озн Вейерштр.

Озн: Нехай { } _n=1 послідовність функції визначено на деякій числовій множині Е . Функціональним рядом називають вираз (1). Візьмемо точку Х₀ і у ряді (1) покладемо Х=X₀ одержемо числовий ряд (2). Ряд (2) може бути як збіжним так і розбіжним.

Озн-я: Якщо ряд(2) збігається, точка Х₀ –точка збіжності функціонального ряду (1). Якщо ряд (2) розбігається то точка Х₀ – точка розбіжності функціонального ряду множини всіх точок збіжності функціонального ряду (1) називається областю збіжності цього ряду.

Зауваження: Зрозуміло , що область збіжності ряду(1) може ,як співпадати з множиною Е так і становити деяку її частину.

Оз-ня: N-ю частиною сумою функціонального ряду (1) називають вираз .

В кожній точці Х ,яка належить області збіжності ряду(1) існує скінченна границя , цю границю називають сумою ряду (1) і пишуть - визначена в області збіжності функціонального ряду (1).

Оз-ня: N- нним залишком функціонального ряду(1) називають вираз

зрозуміло, що для всіх точок Х з області збіжності ряду(1)

Зауваження: Відомо, що сума скінченого числа неперервной ф-й є ф-ю неперервною.Крім того сума скінченого числа ф-ї, можно почлено диференцюювати та інтегрувати. (якщо існують відповідні похідні і інтеграли). Виявляеться, що властивості незавжди виконуються для суми нескінченого числа доданків для ф-них рядів. Однак всі ці властивості зберігаються для так званих рівномірно збіжних ф-них рядів.

Оз-ня: Ф-ний ряд (1) наз. збіжним на деякій множині D E, якщо існуе N=N(E) і незалежить від Х, що для n>N, D виконуеться / (х)/< E.

Основні властивості рівномірного збіжних ф-них рядів:

1. Якщо членами ф-ного ряду (1) є неперервні ф-цій на деякій множині D і цей ряд рівномірно збігаеться то його сума є ф-ю неперервною на множині D.

2. Якщо ф-ний ряд (1) рівномірно збігаеться на [a;b] і його члени є неперервні на цому відрізку ф-й то ряд (1) можна почлено інтегрувати у межах [ , ] [a,b] тобто: S(х)dx= (x)dx= (x)dx

3. Якщо ряд (1) збігаеться на відрізку [a;b] а ряд складених з його похідних (х)

рівномірно збігаеться на [a;b] і крім того ф-й [a;b], /N то ряд (1) можна почлено диференцюювати, тобто: (x)= = , [a;b]

Теорема: (Ознака Верштрасе) Ф-ний ряд один абсолютно і рівномірно, зберігаеться на [a;b] , якщо для /N виконуеться нерівність / / , х [a;b] де ряд збіжний додатній числовий ряд.

Дов. З умови три і ознаки порівняння випливае, що ряд (1) є абсолютно збіжним на відрізку [a;b] . Покажемо теперь рівномірну збіжність ряду (1) . Оскільки ряд (1) абсолютно збігаеться то абсолютним буде його залишок: = ,

де -n-ий залишок ряду відомо, що коли числовий ряд збігаеться його залишок при n прямуе до 0.Дісно, якщо n , тоді >0

>N E Звідси для всіх виконуеться нерівність / (х)/<E Це означае, що ряд (1) є рівномірно збіжним на [a;b]

Приклад: Дослідити на рівномірну збіжність ф-ий ряд: виконуеться нерівність Ряд збігаеться за ознакою Доломбера:

,

g=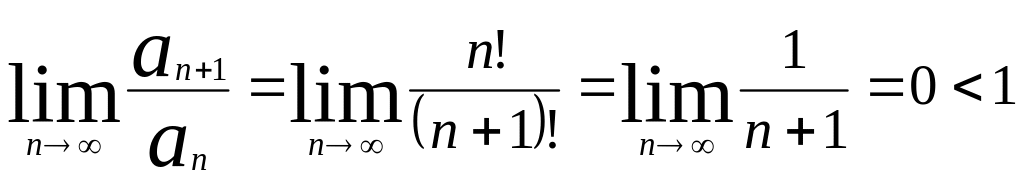

Таким чином вказаний ф-ний ряд рівномірно збігаеться за ознакою Верштрасе на всій числовій осі.

13. Поняття степеневого ряду. Теорема Абелья. Інтервал та радіус збіжності степеневого ряду.

Озн: Степеневим рядом наз. Ф-ний ряд віду (1)

де , дійсні числа, які наз. коефіціентами ряду. Степеневим рядом за степеннями двохчлена наз. ф-ним рядом виду (2)

Зауваження 1: Заміною завжди можно перейти від степеневого ряду (2) до ряду (1) тому надалі будемо розглядати лише степеневі ряди вигляду (1)

Зауваження 2: Всякий степеневий ряд вигляду (1) завжди збіжний в точці х=0 і його сума Таким чином область збіжності ряду (1) завжди містить принаймні одну точку.

Теорема1(Абелья) Якщо степеневий ряд (1) збігаеться в точці то він абсолютно збігаеться для всіх