
- •1.Функція багатьох змінних. Границя функції багатьох змінних.
- •2. Неперервність ф-ї багатьох змінних.
- •3.Частинні похідні. Диференцируємость ф-ї багатьох змінних.
- •4.Повний диференціал ф-ї багатьох змінних. Диференціали вищих порядків.
- •5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.
- •6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.
- •7. Невласні інтеграли 1 роду. Приклади.
- •8. Невласні інтеграли 2-го роду.
- •9.Числові ряди Найпростіші властивості.
- •10.Ознаки порівняння додатніх числових рядів.Приклади.
- •11. Знакоочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.
- •Теорема2(Абелья) Якщо ряд (1) розбіжний в точці то він буде розбіжним для всіх
- •14.Ряд Тейлора
- •14.2Разложение элементарн. Функций в ряд Макларена
- •15 Тригонометрический ряд Фурье.
3.Частинні похідні. Диференцируємость ф-ї багатьох змінних.
Нехай ф-я z=f(x,y) визначена на околі точки М(x,y), надамо змінній х приріст х, залишаючи при цьому змінну у незмінною, так щоб точка М1(х+х,у) належала заданому околу точки М.
Означення: Величина хz= f(х+х,у)-f(x,y) – частинний приріст ф-ї z=f(x,y) по змінній х в т. М(x,y).
Аналогічно визначається частинний приріст змінної у уz= f(х,у+у)-f(x,y).
Означення:
Якщо існує границя
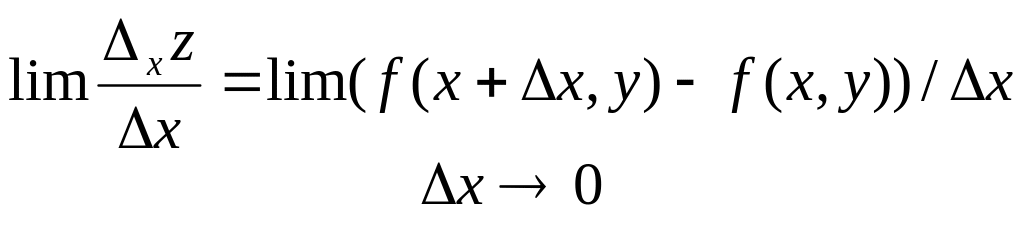 , то її називають частиною похідної
ф-ї z=f(x,y)
по змінній х в точці М(х,у) і позначають
одним з символів: f/x,
z/x,
f’x,z’x.
, то її називають частиною похідної
ф-ї z=f(x,y)
по змінній х в точці М(х,у) і позначають
одним з символів: f/x,
z/x,
f’x,z’x.
Частинну похідну по змінній х в т. М0(х0, у0) позначають f(х0,у0)/x, z’xМ0.
Аналогічно
визначається частинна похідну по
змінній у:
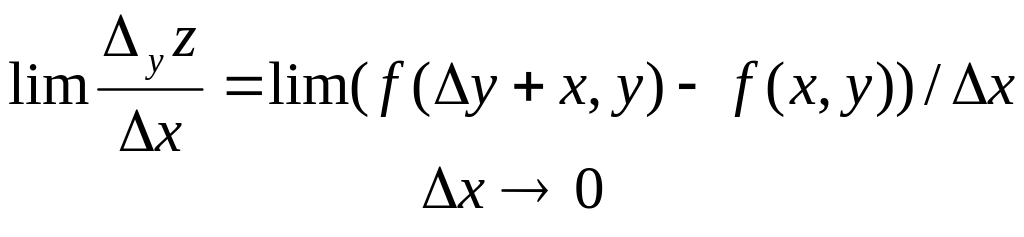 .
.
Заув-я Згідно з озн-м при знаходженні похідної z’x обчисл. Звичайну похідну 1 змінної по х вважаючи у-const. Тому для обчислення частинних похідних справедливі формули : правила диф-ня ф-ї однієї змінної. Похідна z’x характеризує швидкість зміни ф-ї z=f(x,y) у напрямі Ох, а z’у-Оу.
Геометричний зміст частинних похідних.
Графіком ф-ї z=f(x,y) є деяка поверхня. Графіком ф-ї z=f(x,y0) є лінія перетину цієї поверхні з площею у=у0. Виходячи з геометричного змісту похідної для ф-ї однієї змінної одержимо що fу(x0,y0)=tgx де х- кут Нірго додатнім напр.. Ох і додатної до кривої z=fу(x,y0) в точці М0(x0,y0, fу(x0,y0).
Аналогічно fу(x0,y0)=tg.
Якщо ф-я z=f(x,y) визначена у деякій області і має частинні похідні z’x і z’у в усіх точках (x,y) D, то її частинні похідні можна розглядати як нові ф-ї що задані в області D.
Озн: Якщо існує частинна похідна по х від ф-ї f /x, то наз-ся частинною похідною 2-го порядку від ф-ї z=f(x,y) по х .
Якщо існує частинна пох-на по у від ф-ї f /у її наз-ть частинною пох-ю 2-го пор-ку по у. Якщо розглядати частинну пох-ну по у від ф-ї f /x, то ця пох-на наз-ся мішаною частинною пох-ю 2-го пор-ку від ф-ї z=f(x,y).
Для ф-ї 2-х змінних можна розг-ти 4 пох-х 2-го порядку : z”xх, z”xу, z”уу, z”ух.
Т-ма:(про мішані похідні)
Якщо ф-я z=f(x,y) визначена із своїми пох-ми z”xх, z”xу, z”уу, z’ух у деякому околі точки М0 , причому z”xу і z’ух неперервні в точці М0 то в цій точці z”xу от м0 до ух = z’ух от м0.
Заув-ня: аналогічна теорема справедлива для будь яких мішаних похідних які неп-ні і відрізняються лише порядком диф-ня.
Приклад:
Знайти пох-ні 2-го порядку
Z=x3-x2y+y3
z’x=3x2-2xy; z’у=-x2+3y2;
z”ух=( z’у) ’x=-2x.
Нехай ф-я z=f(x,y) визначена в деякому околі точки М(x,y), надамо змінним х та у приріст х,у, так щоб точка М1(х+х,у+у) належала вказаному околу і розглянемо повний приріст точки М.
Означення: Величина хz= f(х+х,у)-f(x,y) – частинний приріст ф-ї z=f(x,y) по змінній ф-ї z=f(x,y) в точці М(x,y) z= f(х+х,у+у)-f(x,y).
Означення: Ф-я z=f(x,y) диференцируєма в точці М, якщо її повний приріст в цій точці можна надати у вигляді z=Ах+Ву+x+y (1), де А,В – дійсні числа, які не залежать від х,у.
х,у), х,у) – нескінченно малі ф-ї, якщо х, у0.
Теорема 1(неперервність диференцируємої ф-ї): Якщо ф-я z=f(М) диференцируєма в точці М, то вона неперервна в цій точці.
Доведення: Якщо ф-я z=f(М) диференцируєма в точці М, то з (1) випливає ,це означає, що ф-я неперервна в точці М( Теорема 2, означення 1’).
Теорема 2(існування частинних похідних диференцируємої ф-ї): Якщо ф-я z=f(x,y) диференцируєма в точці М(х,у), то вона має в цій точці частинні похідні fx’(x,y)= fx’, fy’=fy’(x,y), z=fx’х+ f’уу+x+y .
Доведення:
Оскільки ф-я z=f(x,y)
диференцируєма в точці М(х,у), то в цій
точці виконується (1). Підставимо у (1)
у=0.
Тоді zх=Ах+(x,0)
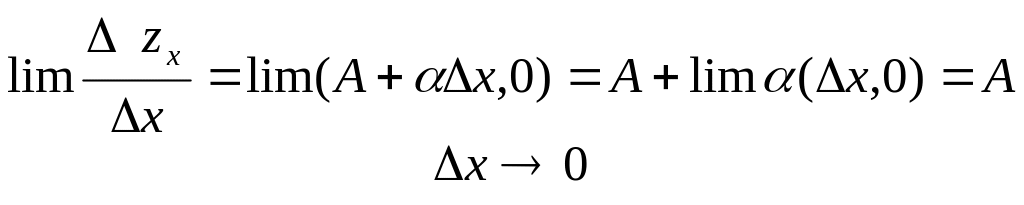 ,
тобто А=
fx’(x,y).
Аналогічно, якщо взяти х=0
і перейти до границі при у0,
одержимо, що В=fy’(x,y).
,
тобто А=
fx’(x,y).
Аналогічно, якщо взяти х=0
і перейти до границі при у0,
одержимо, що В=fy’(x,y).
З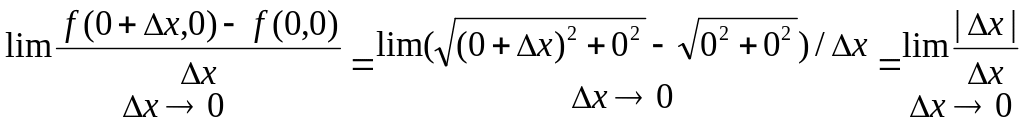 ауваження:
Твердження обернені до теорем 1 і 2 в
загальному випадку не виконуються.
Тобто з неперервності f(x,y),
а також з існування її частинних похідних
у т. М ще не випливає диференцируємость
ф-ї.
ауваження:
Твердження обернені до теорем 1 і 2 в
загальному випадку не виконуються.
Тобто з неперервності f(x,y),
а також з існування її частинних похідних
у т. М ще не випливає диференцируємость
ф-ї.
Приклад: z=(х2+у2)1/2, ф-я z неперервна в точці (0,0), але недиференцируєма в цій точці: границі не існує, тому, не існує і похідної fx’(0,0), аналогічно не існує fy’(0,0), тому за теоремою 2 ф-я z недиференцируєма.
Теорема 3(достатні умови диференцируємості): Якщо ф-я z=f(x,y) у деякому околі т. М має частинні похідні і вони неперервні в т. М, то ф-я z=f(x,y) диференцируєма в точці М.
Д![]() оведення:
Надамо змінним х та у приріст х,у0,
так щоб точка М1(х+х,у+у)
належала вказаному околу і розглянемо
повний приріст ф-ї в точці М. z=
f(х+х,у+у)-f(x,y)=f(х+х,у+у)-f(x,y+у)+f(x,y+у)-f(x,y)=теорема
Лагранжа=f’(x+1х,у+у)х+
fy’(x,y+2у)у
(2), де 0102.
Тут ми використовуємо теорему Лагранжа
(оскільки дана ф-я має частинні похідні).
Оскільки частинні похідні неперервні
в т. М, то
оведення:
Надамо змінним х та у приріст х,у0,
так щоб точка М1(х+х,у+у)
належала вказаному околу і розглянемо
повний приріст ф-ї в точці М. z=
f(х+х,у+у)-f(x,y)=f(х+х,у+у)-f(x,y+у)+f(x,y+у)-f(x,y)=теорема
Лагранжа=f’(x+1х,у+у)х+
fy’(x,y+2у)у
(2), де 0102.
Тут ми використовуємо теорему Лагранжа
(оскільки дана ф-я має частинні похідні).
Оскільки частинні похідні неперервні
в т. М, то
 випливає з неперервності. Аналогічно
випливає з неперервності. Аналогічно
 випливає з неперервності. Тоді
f’(x+1х,у+у)=fх’(x,у)+(x,y);
fy’(x,y+2у)=fу’(x,у)+(x,y),
де (x,y)
і (x,y)-
нескінченно малі ф-ї при х,
у0.
Підставляючи ці вирази у рівність (2),
одержимо z=fx’(х,у)х+
fу’(х,у)у+(x,y)x+(x,y)y,
а це і означає, що ф-я f(x,y)
диференцируєма в т. М.
випливає з неперервності. Тоді
f’(x+1х,у+у)=fх’(x,у)+(x,y);
fy’(x,y+2у)=fу’(x,у)+(x,y),
де (x,y)
і (x,y)-
нескінченно малі ф-ї при х,
у0.
Підставляючи ці вирази у рівність (2),
одержимо z=fx’(х,у)х+
fу’(х,у)у+(x,y)x+(x,y)y,
а це і означає, що ф-я f(x,y)
диференцируєма в т. М.
Наслідок: Щоб ф-я f(x,y) була диференцируєма в точці необхідно, щоб вона мала в цій точці частинні похідні і достатньо щоб вона мала в цій точці неперервні частинні похідні.
