Критерий согласия Колмогорова
Критерий согласия Колмогорова отличается своей простотой и находит широкое применение в исследовании надежности машин и их элементов. Для его применения на графике строится эмпирическая функция распределения F*(x,) и выбранная аппроксимирующая функция F(x) предполагаемого закона распределения. При этом за меру расхождения между F*(x,) и F(x) выбирается величина:
где
= max | F(x)
- F*(x) | - максимальное расхождение между
опытной и теоретической плотностями
вероятности случайных величин;
N— объем статистических данных.
На основе специальных таблиц
определяется
вероятность Р (
)того,
что если конкретный вариационный признак
распределен по рассматриваемому
теоретическому распределению, то из-за
чисто случайных причин максимальное
расхождение между фактическими и
теоретическими накопленными частотами
будет не меньшим, чем фактически
наблюдаемое. По результатам вычислений
величины Р (
) делают следующие выводы:
1. Если вероятность Р ( ) достаточно велика, то гипотезу
о том, что фактическое распределение близко к теоретическому,
можно считать подтвержденной;
2. Если же вероятность Р ( ) мала - гипотеза отвергается.
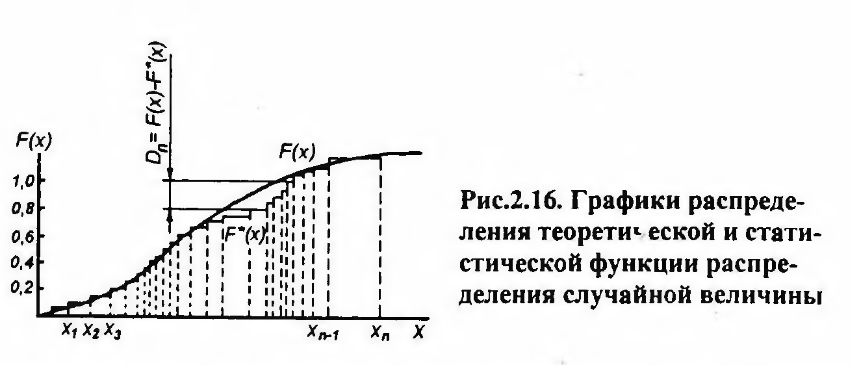
Так, если < 1,0, то принятый теоретический закон не противоречит эмпирическому.
Границы критической области для критерия Колмогорова зависят от объема выборки: чем меньше число результатов наблюдений, тем выше необходимо устанавливать критическое значение вероятности. Если число отказов при наблюдении составило N= 10... 15, то Р( )> 0,5, если N> 100, то Р( ) = 0,01. ..0,05.
Критерий Колмогорова рекомендуется применять, если параметры распределения F(x) известны до опыта и ставится задача по результатам эксперимента проверить только согласованность теоретического и опытного распределения.
Большим достоинством критерия Колмогорова является возможность оценки справедливости гипотезы при малых объемах наблюдений случайной величины. Однако необходимо отметить, что при больших объемах наблюдений (N> 100) лучше пользоваться критерием Пирсона
Пример. В результате наблюдений получено 170 значений случайной величины х. Наибольшее расхождение между теоретическим и расчетным значениями функции F(x) составляет: Dn = max |F(x) - F*(x)| = 0,0149. Необходимо оценить принадлежность распределения к нормальному закону.
Решение. Вычисляем значение параметра :
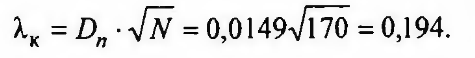
Из таблицы находим значение вероятности Р( ) : Р (0,194) = 1,0.
Таким образом Р( )>0,05 и гипотеза о нормальном законе распределения случайной величины справедлива.
Критерий согласия Пирсона
Критерий
Пирсона
2
(хи) является наиболее состоятельным
при большом цикле наблюдений. Его
состоятельность состоит в том, что он
почти всегда опровергает неверную
гипотезу и обеспечивает минимальную
ошибку в принятии неверной гипотезы по
сравнению с другими критериями. Этот
критерий следует применять в тех случаях,
когда теоретические значения параметров
функции распределения случайной величины
неизвестны.
Критерий согласия Пирсона 2 определяется по уравнению:
где
-
число интервалов укрупненного
статистического ряда;
m, - опытная частота в i-ом интервале статистического ряда;
-
теоретическая частота в i-ом
интервале.
Теоретическая частота:
где N- число точек информации;
F(t)
и F(
)
- интегральные функции i-го
и (i
- 1)-го интервалов статистического ряда.
Полученное
значение
2
сравнивают с критическим (табличным)
значением
(r)
этого критерия. Значение
(r)
определяется по специальным
математико-статистическим таблицам в
зависимости от числа степеней свободы
r,
уровня значимости а или доверительной
вероятности Р (см. табл.)
Доверительной считается такая вероятность, которую можно признать достаточной для суждения о достоверности характеристик, полученных на основе выборочных наблюдений. В качестве доверительной вероятности принимают значения 0,95; 0,99; 0,999. Последняя обеспечивает более надежные выводы. Для инженерных расчетов приемлемой является доверительная вероятность Р = 0,95.
Число степеней свободы определяется по формуле:
где s - количество параметров теоретического распределения (для нормального закона s = 1, для экспоненциального и распределения Вейбулла - s = 2).
- число интервалов укрупненного статистического ряда;
Гипотезу о предполагаемом законе распределения считают справедливой при условии 2 < (r) Если 2 >= (r) , то гипотезу отвергают.
Недостатком критерия Пирсона 2 является то, что он не дает однозначной оценки для заключения об оптимальности принятого теоретического закона распределения. Кроме того, применение критерия 2 эффективно при числе результатов наблюдений N>30.