Инвертор

Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).

Применение логических элементов

Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.

Комбинационные логические устройства

Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами.

• Шифратор

• Дешифратор

• Мультиплексор

• Демультиплексор

• Полусумматор

• Сумматор

Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.

Последовательностные цифровые устройства

Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.

• Триггер

• Счётчик импульсов

• Регистр

• Венъюнктор

• Секвентор

30. Линии с потерями. Телеграфные уравнения. Причины искажения сигналов в линиях с потерями.

Телеграфные уравнения - пара линейных дифференциальных уравнений, описывающих распределение напряжения и тока в линии электропередачи по времени и расстоянию. Уравнения были составлены Оливером Хевисайдом, в 1880-х разработавшим модель линии электропередачи, описанную в этой статье. Теория Хевисайда применима к линиям электропередачи всех частот, включая высокочастотные линии (такие, как телеграфные и радиочастотные проводники), линии со звуковыми частотами (например, телефонные линии), низкочастотные линии (например, силовые линии) и постоянный ток.

Уравнения

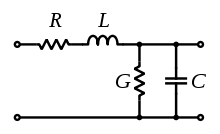
Схематическое изображение элементарных компонентов линии электропередачи.

Телеграфные уравнения, как и все другие уравнения, описывающие электрические явления, могут быть сведены к частному случаю уравнений Максвелла. С точки зрения практики, предполагается, что проводники состоят из бесконечной цепи двухполюсников, каждый из которых представляет собой бесконечно короткий участок линии:

• Удельное сопротивление проводников R представлено в виде резистора (выражается в Омах на единицу длины).

• Удельная индуктивность L (возникает из-за магнитного поля вокруг проводников, самоиндуктивности и т.д.) представлена в виде катушки (генри на единицу длины).

• Емкость C между двумя проводниками представлена в виде конденсатора (фарад на единицу длины).

• Проводимость диэлектрического материала, разделяющего два проводника (изоляции) G представлена в виде резистора между проводом под напряжением и нулевым проводом (сименс на единицу длины). В модели этот резистор имеет сопротивление 1 / G Ом.

Для ясности повторим, что модель основана на бесконечной цепи элементов, показанных на картинке, и номиналы ее частей указаны на единицу длины. Также можно использовать R', L', C' и G', чтобы подчеркнуть, что значения являются производными по координате.

Телеграфные уравнения выведены в той же форме в следующих источниках:: ^[1], ^[2], ^[3], ^[4], ^[5], ^[6], ^[7]