[Править]Различные постановки задачи Коши

• ОДУ первого порядка, разрешённое относительно производной

• Система   ОДУ первого порядка, разрешённая относительно производных (нормальная система  -го порядка)

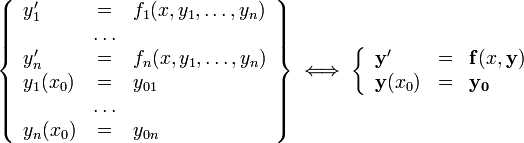
• ОДУ  -го порядка, разрешённое относительно старшей производной

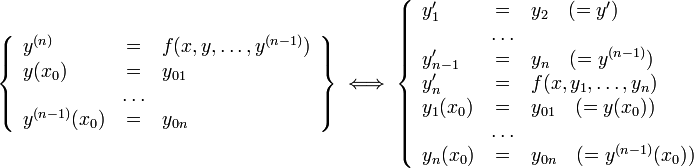
12 Дифференциальные уравнения с разделяющимися переменными

Определение и способ решения

Пусть   — некоторая функция,   — ее производная. Для удобства будем записывать производную виде  , имеющем смысл отношения бесконечно малых приращений — дифференциалов. Дифференциал   — приращение значения переменной в окрестности  , стремящееся к нулю. Дифференциал функции   — малое приращение функции,  . Пусть   и   — некоторые функции от   и  . Рассмотрим уравнение

.

Уравнение такого вида называется обыкновенным дифференциальным уравнением с разделяющимися переменными. Умножим его на  :

.

Последнее равенство означает, что малые приращения левой и правой частей равны. Поэтому их суммы также равны. Предположим что при     и возьмем интегралы от левой и правой частей. Пределы интегрирования — от   до   для левой части и от   для   для правой части уравнения:

.

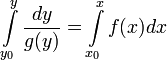Решая получившееся в результате интегрирования алгебраическое уравнение, мы можем выразить  .

Значения   и   называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных —  , где   — первообразная  ,   — произвольная постоянная, запишем это в виде

.

Следует отметить, что у дифференциального уравнения с разделяющимися переменными могут существовать так называемые нулевые решения — постоянные  , удовлетворяющие уравнению  . При них равны нулю как правая, так и левая части дифференциального уравнения (поскольку производная константы равна нулю).

[править]Пример 1

Решить дифференциальное уравнение  .

Разделим переменные:

.

Т. к. начальные условия не заданы, возьмем неопределенный интеграл от обеих частей уравнения:

,

.

Осталось лишь выразить   через  :

.

Найдем также нулевые решения:

.

Ответ:  .

13 Однородное дифференциальное уравнение

Существует два понятия однородности дифференциальных уравнений.

[править]1

Обыкновенное уравнение первого порядка   называется однородным относительно x и y, если функция   является однородной степени 0:

.

Однородную функцию можно представить как функцию от  :

.

Используем подстановку  , а затем воспользуемся правилом произведения :  . Тогда, дифференциальное уравнение  сводится к уравнению с разделяющимися переменными:

.

[править]2

Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение   — однородно, если  .

В случае, если  , говорят о неоднородном дифференциальном уравнении.

Именно для решения линейных однородных диф. уравнений была построена целая теория, чему способствовало выполнение у них принципа суперпозиции.

[править]См. также

14 линейные дифференциальные уравнения первого порядка

Обыкновенное дифференциальное уравнение вида

называется линейным дифференциальными уравнениями. Для его решения обычно используют метод вариации постоянной. Для этого сначала необходимо решить соответствующее однородное дифференциальное уравнение

которое является дифференциальным уравнением с разделяющимися переменными.Полученное общее решение   этого уравнения надо подставить в исходноеобыкновенное дифференциальное уравнение, неоднородное дифференциальное уравнение, считая, что   . Затем необходимо решить полученное обыкновенное дифференциальное уравнение относительно неизвестной функции   и подставить его решение в ранее полученную формулу   .

Чтобы решить уравнение Бернулли вида

необходимо сделать замену переменной   . После замены будет получено линейное дифференциальное уравнение.