
- •Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Определение
- •Определение
- •[Править]Сходимость числовых рядов
- •[Править]Необходимый признак сходимости ряда
- •Знакочередующийся ряд
- •[Править]Признак Лейбница
- •[Править]Оценка остатка ряда Лейбница
- •Степенной ряд
- •[Править]Пространство степенных рядов
- •[Править]Сходимость степенных рядов
- •[Править]Признаки сходимости
- •Ряд Тейлора
- •[Править]Определение
- •[Править]Связанные определения
- •[Править]Свойства
- •[Править]Формула Тейлора
- •[Править]Различные формы остаточного члена
- •Ряды Маклорена некоторых функций
- •8 Ряды фурье Ряд Фурье
- •10 Двойной Интегралл Двойной интеграл
- •11 Понятие о дифференциальном уравнении. Задача Коши
- •Задача Коши
- •[Править]Различные постановки задачи Коши
- •12 Дифференциальные уравнения с разделяющимися переменными
- •13 Однородное дифференциальное уравнение
- •15 Линейное дифференциальное уравнение с постоянными коэффициентами
- •[Править]Однородное уравнение [править]Уравнение порядка n
- •[Править]Уравнение второго порядка
- •Тандартная модель
- •Действия над комплексными числами
Ряд Тейлора
[править]
Материал из Википедии — свободной энциклопедии
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а такжеНьютон.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Содержание [убрать]
|
[Править]Определение
Пусть
функция ![]() бесконечно
дифференцируема в некоторой окрестности точки
бесконечно
дифференцируема в некоторой окрестности точки ![]() .
Формальный ряд
.
Формальный ряд

называется
рядом Тейлора функции ![]() в
точке
.
в
точке
.
[Править]Связанные определения
В случае, если
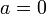 ,
этот ряд также называется рядом Макло́рена.
,
этот ряд также называется рядом Макло́рена.
[Править]Свойства
Если есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке области определения сходится к в некоторой окрестности .
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности . Например, Коши предложил такой пример:
![]()
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке равны нулю.
[Править]Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции вокрестности некоторой точки.
Теорема:
-
Пусть функция имеет
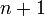 производную в
некоторой окрестности
точки
,
производную в
некоторой окрестности
точки
, 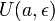
Пусть

Пусть
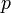 —
произвольное положительное число,
—
произвольное положительное число,
тогда:
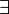 точка
точка 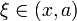 при
при 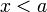 или
или 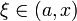 при
при 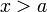 :
: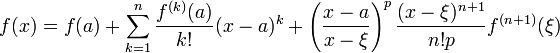
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
[Править]Различные формы остаточного члена
В форме Лагранжа:
![]()
В форме Коши:
![]()
В интегральной форме:

Ослабим предположения:
Пусть функция имеет
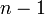 производную
в некоторой окрестности точки
производную
в некоторой окрестности точки
И производную в самой точке , тогда:
![]() —
остаточный
член в асимптотической форме (в
форме Пеано,
в локальной фо
—
остаточный
член в асимптотической форме (в
форме Пеано,
в локальной фо
Ряды Маклорена некоторых функций
Экспонента:
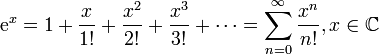
Натуральный логарифм:
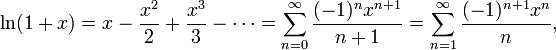 для
всех
для
всех ![]()
Биномиальное разложение:
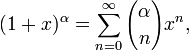 для
всех
и
всех комплексных
для
всех
и
всех комплексных ![]() где
где
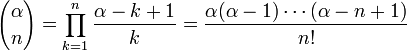
В частности:
Квадратный корень:
![]() для
всех
для
всех
![]() для
всех
для
всех
Конечный геометрический ряд:
![]() для
всех
для
всех ![]()
Тригонометрические функции:


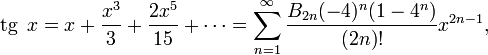 для
всех
для
всех ![]() где
где ![]() — Числа
Бернулли
— Числа
Бернулли
![]() для
всех
для
всех ![]() где
— Числа
Бернулли
где
— Числа
Бернулли
![]() для
всех
для
всех
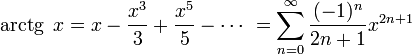 для
всех
для
всех
Гиперболические функции:

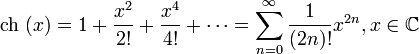
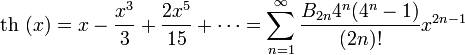 для
всех
для
всех
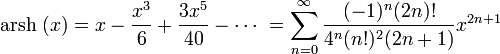 для
всех
для
всех
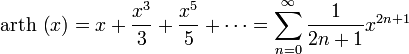 для
всех
для
всех
8 Ряды фурье Ряд Фурье
[править]
Материал из Википедии — свободной энциклопедии

Добавление членов ряда Фурье
Ряд Фурье —
представление произвольной функции
с
периодом ![]() в
виде ряда
в
виде ряда

Этот ряд может быть также переписан в виде
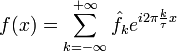 .
.
где
![]() —
амплитуда k-го
гармонического колебания,
—
амплитуда k-го
гармонического колебания,
![]() —
круговая
частота гармонического колебания,
—
круговая
частота гармонического колебания,
![]() —
начальная
фаза k-го
колебания,
—
начальная
фаза k-го
колебания,
![]() — k-я
комплексная амплитуда
— k-я
комплексная амплитуда
В более общем виде рядом Фурье элемента гильбертова пространства называется разложение этого элемента по ортогональному базису. Существует множество системортогональных функций: Уолша, Лагера, Котельникова и др.
Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя придифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.
