
- •Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Определение
- •Определение
- •[Править]Сходимость числовых рядов
- •[Править]Необходимый признак сходимости ряда
- •Знакочередующийся ряд
- •[Править]Признак Лейбница
- •[Править]Оценка остатка ряда Лейбница
- •Степенной ряд
- •[Править]Пространство степенных рядов
- •[Править]Сходимость степенных рядов
- •[Править]Признаки сходимости
- •Ряд Тейлора
- •[Править]Определение
- •[Править]Связанные определения
- •[Править]Свойства
- •[Править]Формула Тейлора
- •[Править]Различные формы остаточного члена
- •Ряды Маклорена некоторых функций
- •8 Ряды фурье Ряд Фурье
- •10 Двойной Интегралл Двойной интеграл
- •11 Понятие о дифференциальном уравнении. Задача Коши
- •Задача Коши
- •[Править]Различные постановки задачи Коши
- •12 Дифференциальные уравнения с разделяющимися переменными
- •13 Однородное дифференциальное уравнение
- •15 Линейное дифференциальное уравнение с постоянными коэффициентами
- •[Править]Однородное уравнение [править]Уравнение порядка n
- •[Править]Уравнение второго порядка
- •Тандартная модель
- •Действия над комплексными числами
Степенной ряд
[править]
Материал из Википедии — свободной энциклопедии
Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
![]()
в
котором коэффициенты
берутся
из некоторого кольца ![]() .
.
-
Содержание
[убрать]
1 Пространство степенных рядов
2 Сходимость степенных рядов
2.1 Признаки сходимости
2.2 См.также
3 Вариации и обобщения
[Править]Пространство степенных рядов
Сюда перенаправляется запрос «Формальный степенной ряд». На эту тему нужна отдельная статья.
Пространство степенных
рядов с одной переменной и коэффициентами
из
обозначается ![]() .
Пространство
имеет
структуру дифференциальной
алгебры над
кольцом
(коммутативной,
целостной, с единицей, если таково же
кольцо
).
Оно часто используется в математике
ввиду того, что в нём легко представимы
и разрешимы формальные
дифференциально-алгебраические и даже
функциональные соотношения (см.
метод производящих
функций).
При его использовании эти соотношения
превращаются в алгебраические уравнения
на коэффициенты рядов. Если они
разрешаются, говорят о получении
формального решения исходной задачи в
виде формального степенного ряда.
.
Пространство
имеет
структуру дифференциальной
алгебры над
кольцом
(коммутативной,
целостной, с единицей, если таково же
кольцо
).
Оно часто используется в математике
ввиду того, что в нём легко представимы
и разрешимы формальные
дифференциально-алгебраические и даже
функциональные соотношения (см.
метод производящих
функций).
При его использовании эти соотношения
превращаются в алгебраические уравнения
на коэффициенты рядов. Если они
разрешаются, говорят о получении
формального решения исходной задачи в
виде формального степенного ряда.
В определены операции сложения, умножения, формального дифференцирования и формальной суперпозиции. Пусть
![]()
Тогда:
![]()
![]()
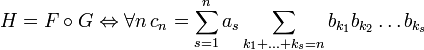 (при
этом необходимо, чтобы соблюдалось
(при
этом необходимо, чтобы соблюдалось ![]() )
)
![]()
[Править]Сходимость степенных рядов
Из
формального степенного ряда с вещественными
или комплексными коэффициентами путем
приписывания формальной
переменной ![]() какого-нибудь
значения в поле вещественных или
комплексных чисел можно получить
числовой ряд. Числовой ряд считается
сходящимся (суммируемым),
если сходится последовательность
частичных сумм, составленных из его
членов, и называется абсолютно
сходящимся,
если сходится последовательность
частичных сумм, составленных из его
членов, взятых по модулю (по норме).
какого-нибудь
значения в поле вещественных или
комплексных чисел можно получить
числовой ряд. Числовой ряд считается
сходящимся (суммируемым),
если сходится последовательность
частичных сумм, составленных из его
членов, и называется абсолютно
сходящимся,
если сходится последовательность
частичных сумм, составленных из его
членов, взятых по модулю (по норме).
[Править]Признаки сходимости
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
Первая теорема Абеля: Пусть ряд
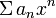 сходится
в точке
сходится
в точке 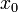 .
Тогда этот ряд сходится абсолютно в
круге
.
Тогда этот ряд сходится абсолютно в
круге 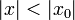 и
равномерно по
и
равномерно по 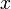 на
любом компактном
подмножествеэтого
круга.
на
любом компактном
подмножествеэтого
круга.
Обращая
эту теорему, получаем, что если степенной
ряд расходится при ![]() ,
он расходится при всех
,
таких что
,
он расходится при всех
,
таких что ![]() .
Из первой теоремы Абеля также следует,
что существует такой радиус
круга
(возможно,
нулевой или бесконечный), что при
.
Из первой теоремы Абеля также следует,
что существует такой радиус
круга
(возможно,
нулевой или бесконечный), что при ![]() ряд
сходится абсолютно (и равномерно по
на
компактных подмножествах круга
),
а при
ряд
сходится абсолютно (и равномерно по
на
компактных подмножествах круга
),
а при ![]() —
расходится. Это значение
называется
радиусом сходимости ряда, а круг
—
кругом сходимости.
—
расходится. Это значение
называется
радиусом сходимости ряда, а круг
—
кругом сходимости.
Формула Коши-Адамара: Значение радиуса сходимости степенного ряда может быть вычислено по формуле:
![]()
(По
поводу определения верхнего предела ![]() см.
статью «Частичный
предел последовательности».)
см.
статью «Частичный
предел последовательности».)
Пусть ![]() и
и ![]() —
два степенных ряда с радиусами
сходимости
—
два степенных ряда с радиусами
сходимости ![]() и
и ![]() .
Тогда
.
Тогда
![]()
![]()
![]()
Если у ряда свободный член нулевой, тогда
![]()
Вопрос
о сходимости ряда в точках границы ![]() круга
сходимости достаточно сложен и общего
ответа здесь нет. Вот некоторые из теорем
о сходимости ряда в граничных точках
круга сходимости:
круга
сходимости достаточно сложен и общего
ответа здесь нет. Вот некоторые из теорем
о сходимости ряда в граничных точках
круга сходимости:
Признак Д’Аламбера: Если при и
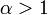 выполнено
неравенство
выполнено
неравенство
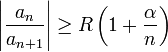
тогда степенной ряд сходится во всех точках окружности абсолютно и равномерно по .
Признак Дирихле: Если все коэффициенты степенного ряда положительны и последовательность монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности
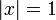 ,
кроме, быть может, точки
,
кроме, быть может, точки 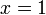 .
.Вторая теорема Абеля: Пусть степенной ряд сходится в точке . Тогда он сходится равномерно по на отрезке, соединяющем точки 0 и .
Сумма степенного ряда как функция комплексного параметра является предметом изучения теории аналитических функций.
