Знакочередующийся ряд

[править]

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 августа 2011; проверки требуют 6 правок.

Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:

[Править]Признак Лейбница

Основная статья: Теорема Лейбница о сходимости знакочередующихся рядов

Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:

Пусть для знакочередующегося ряда выполняются следующие условия: 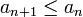 (монотонное невозрастание {an} по абсолютной величине)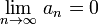 . Тогда этот ряд сходится.

Замечания:

Проверить информацию. Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье. На странице обсуждения должны быть пояснения.

Если, выполнены все условия, и ряд из модулей ( ) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность   существенна.

Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.

Пример

. Ряд из модулей имеет вид   — это гармонический ряд, который расходится.

Теперь воспользуемся признаком Лейбница:

1. знакочередование выполнено 

2. 

3. .

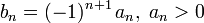
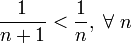
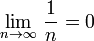Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.

[Править]Оценка остатка ряда Лейбница

Из доказательства признака Лейбница следует, что сумма знакопеременного сходящегося ряда меньше по модулю первого члена остатка ряда. Поскольку любой остаток ряда r_nявляется также рядом Лейбница, то для него справедливо:

.

6 абсолютная и условная сходимость знакопеременного ряда

Абсолютная и условная сходимость Ряд   называется абсолютно сходящимся, если ряд   также сходится.  Если ряд   сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.  Ряд   называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Пример 1

Исследовать на сходимость ряд  . Решение. Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем        поскольку  . Следовательно, данный ряд сходится.

Пример 2

Исследовать на сходимость ряд  . Решение. Попробуем применить признак Лейбница:        Видно, что модуль общего члена не стремится к нулю при n → ∞. Поэтому данный ряд расходится .

7 понятие степенного ряда.Ряд Тейлора,Маклорена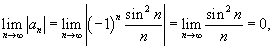
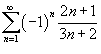