Корреляционный анализ

- математико-статистический метод выявления наличия корреляционной зависимости между компонентами многомерной случайной величины, определения силы и направления их связи.

Предпосылки корреляционного анализа

При построении корреляционных моделей исходят из выполнения условий случайности результатов наблюдений и нормальности закона распределения анализируемой многомерной генеральной совокупности.

Понятие "корреляционная зависимость"

Корреляционной зависимостью случайной величины Y от случайных величин X₁, X₂,…, X_k называется функциональная зависимость условного математического ожидания M(Y/x₁,x₂,…,x_k) величины Y от значений x₁, x₂,…, x_k переменных X₁, X₂,…, X_k:

M(Y/x₁,x₂,…,x_k)=f(x₁,x₂,…,x_k).

Функция f(x₁,x₂,…,x_k), устанавливающая зависимость условного математического ожидания M(Y/x₁,x₂,…,x_k) случайной величины Y от значений x₁, x₂,…, x_k случайных переменных X₁, X₂,…, X_k, называется функцией регрессии случайной величины Y на случайный вектор (X₁, X₂,…, X_k).

Аналитическое представление корреляционной зависимости в виде M(Y/x₁,x₂,…,x_k)=f(x₁,x₂,…,x_k) называется уравнением регрессии случайной величины Y на случайный вектор (X₁,X₂,…,X_k).

Двумерная корреляционная модель

Исследуется зависимость между признаками X, Y. Предполагается, что распределение случайного вектора (X,Y) подчинено закону Гаусса: плотность совместного распределения случайных величин X, Y определяется формулой:

.

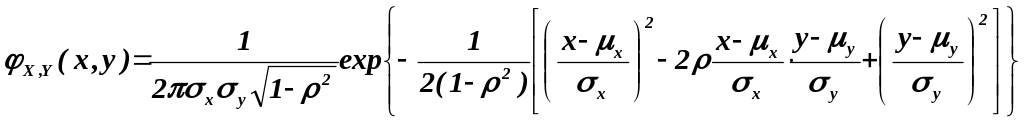Параметры двумерного нормального распределения имеют следующий теоретико-вероятностный смысл:

μ_x - математическое ожидание величины X;

μ_y - математическое ожидание величины Y;

σ_x – среднее квадратическое отклонение величины X;

σ_y - среднее квадратическое отклонение величины Y;

ρ - коэффициент корреляции между признаками X, Y.

Коэффициент корреляции как мера стохастической связи

Если ρ_xy=0, то плотность распределения вектора (X,Y) приобретает вид:

,

т.е. φ_X,Y(x,y)=φ_X(x)φ_Y(y), что означает независимость случайных величин X, Y.

Таким образом, в рамках корреляционного анализа понятия некоррелированности и независимости эквивалентны, что дает основание рассматривать коэффициент корреляции ρ_xy в качестве меры стохастической связи признаков X, Y.

Уравнение линейной парной регрессии

Из курса теории вероятностей известно, что

,

При этом условная плотность величины Y определяется на основании выражения:

.

Используя представления φ_X,Y(x,y), φ_X(x) для нормально распределенных случайных величин (X,Y), X и осуществляя соответствующее интегрирование, получаем уравнение линейной парной регрессии Y на X:

или ,

где - коэффициент регрессии Y на X.

Из вида уравнения линейной парной регрессии следует, что график функции регрессии есть прямая линия.

Замечание

В случае , т.е. некоррелированности X, Y, прямая линия регрессии Y на X параллельна координатной оси .

Положительный знак коэффициента корреляции означает, что прямые линии регрессии имеют в координатной плоскости положительный тангенс угла наклона, с увеличением (или уменьшением) значения X пропорционально в среднем возрастает (соответственно убывает) значение переменной Y.

Отрицательный знак коэффициента корреляции указывает на обратную тенденцию.

Парный коэффициент детерминации

Степень рассеяния значений Y относительно линии регрессии Y на X характеризуют условная дисперсия:

.

Расчет по этой формуле дает следующее выражение:

.

Квадрат коэффициента корреляции называется парным коэффициентом детерминации.