
- •Высшая математика Основные теоремы и определения
- •Свойства рядов.
- •Критерий Коши.
- •Степенные ряды.
- •Признак сравнения рядов с неотрицательными членами.
- •Ряд Тейлора.
- •Предельный признак Даламбера.
- •Нормальные системы обыкновенных дифференциальных уравнений.
- •Знакочередующиеся ряды.
- •Абсолютная и условная сходимость рядов.
- •Свойства абсолютно сходящихся рядов.
- •Тригонометрический ряд.
- •Функциональные ряды.
- •Разложение в ряд Фурье непериодической функции.
- •Свойства равномерно сходящихся рядов.
- •Ряды Фурье для функций любого периода.
- •Список литературы
Высшая математика Основные теоремы и определения
Определение.
Сумма членов бесконечной числовой
последовательности
 называется числовым рядом.
называется числовым рядом.

При
этом числа
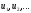 будем называть членами ряда, аun
– общим членом ряда.
будем называть членами ряда, аun
– общим членом ряда.
Определение.
Суммы
 ,
n
= 1, 2, …
называются частными (частичными) суммами
ряда.
,
n
= 1, 2, …
называются частными (частичными) суммами
ряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, …,Sn, …
Определение.
Ряд
 называется сходящимся, если сходится
последовательность его частных сумм.
Сумма сходящегося ряда – предел
последовательности его частных сумм.
называется сходящимся, если сходится
последовательность его частных сумм.
Сумма сходящегося ряда – предел
последовательности его частных сумм.

Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
Свойства рядов.
1) Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.
2)
Рассмотрим два ряда
 и
и ,
где С – постоянное число.
,
где С – постоянное число.
Теорема.
Если
ряд
 сходится
и его сумма равнаS,
то ряд
сходится
и его сумма равнаS,
то ряд
 тоже
сходится, и его сумма равна СS.
(C
0)
тоже
сходится, и его сумма равна СS.
(C
0)
3)
Рассмотрим два ряда
 и
и .
Суммой или разностью этих рядов будет
называться ряд
.
Суммой или разностью этих рядов будет
называться ряд ,
где элементы получены в результате
сложения (вычитания) исходных элементов
с одинаковыми номерами.
,
где элементы получены в результате
сложения (вычитания) исходных элементов
с одинаковыми номерами.
Теорема.
Если
ряды
 и
и сходятся
и их суммы равны соответственноS
и , то ряд
сходятся
и их суммы равны соответственноS
и , то ряд
 тоже сходится и его сумма равнаS
+ .
тоже сходится и его сумма равнаS
+ .

Разность двух сходящихся рядов также будет сходящимся рядом.
Сумма сходящегося и расходящегося рядов будет расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Критерий Коши.
(необходимые и достаточные условия сходимости ряда)
Для
того, чтобы последовательность
 была
сходящейся, необходимо и достаточно,
чтобы для любого
была
сходящейся, необходимо и достаточно,
чтобы для любого существовал такой номерN,
что при n
> N
и любом p
> 0, где р – целое число, выполнялось
бы неравенство:
существовал такой номерN,
что при n
> N
и любом p
> 0, где р – целое число, выполнялось
бы неравенство:
 .
.
1.3
Определение. Ряд
 называется
равномерно сходящимся на отрезке [a,b],
если равномерно сходится на этом отрезке
последовательность частных сумм этого
ряда.
называется
равномерно сходящимся на отрезке [a,b],
если равномерно сходится на этом отрезке
последовательность частных сумм этого
ряда.
Теорема. (Критерий Коши равномерной сходимости ряда)
Для
равномерной сходимости ряда
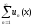 необходимо
и достаточно, чтобы для любого числа
>0 существовал такой номерN(),
что при n>N
и любом целом p>0
неравенство
необходимо
и достаточно, чтобы для любого числа
>0 существовал такой номерN(),
что при n>N
и любом целом p>0
неравенство

выполнялось бы для всех х на отрезке [a,b].
Теорема. (Признак равномерной сходимости Вейерштрасса)
(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)
Ряд
 сходится
равномерно и притом абсолютно на отрезке
[a,b],
если модули его членов на том же отрезке
не превосходят соответствующих членов
сходящегося числового ряда с положительными
членами :
сходится
равномерно и притом абсолютно на отрезке
[a,b],
если модули его членов на том же отрезке
не превосходят соответствующих членов
сходящегося числового ряда с положительными
членами :

т.е. имеет место неравенство:
 .
.
Еще
говорят, что в этом случае функциональный
ряд
 мажорируется числовым рядом
мажорируется числовым рядом .
.
ряд
 называется положительным, если Un≥0,
для всех n
€ N
называется положительным, если Un≥0,
для всех n
€ N
Интегральный признак Коши.
Если
(х) – непрерывная положительная функция,
убывающая на промежутке
[1;), то
ряд (1)
+ (2) + …+ (n)
+ … =
 и несобственный интеграл
и несобственный интеграл
 одинаковы в смысле сходимости.
одинаковы в смысле сходимости.
Пример.
Ряд
 сходится при >1 и расходится 1 т.к.
соответствующий несобственный интеграл
сходится при >1 и расходится 1 т.к.
соответствующий несобственный интеграл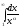 сходится при >1 и расходится 1. Ряд
сходится при >1 и расходится 1. Ряд называется общегармоническим рядом.
называется общегармоническим рядом.
Следствие.
Если f(x)
и (х) – непрерывные функции на интервале
(a,
b]
и
 то интегралы
то интегралы и
и ведут себя одинаково в смысле сходимости.
ведут себя одинаково в смысле сходимости.
