6 Исследование робастности полученной зс методом в.Л.Харитонова

Интервальная матрица состояния спроектированной ЗС имеет вид:

Матрица имеет интервальный характеристический полином (ИХП)

где

Полиномы В.Л.Харитонова в этом случае записываются в форме:

Нетрудно увидеть, что, в силу положительности коэффициентов, все полиномы Л.В.Харитонова являются гурвицевыми, а, следовательно, гурвицевым является и ИХП . А это, по теореме В.Л.Харитонова, означает, что полученная в пункте 5 замкнутая система робастно устойчива.

7 Синтез параметрически инвариантной системы

Дано ВМО ВСВ НОУ с интервальными матричными компонентами в форме

,

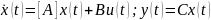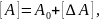
получаемое с использованием интервальной арифметики на основе интервальной реализации параметров 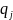, записываемых в форме 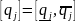при следующих граничных (угловых) значениях:

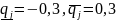
Формирование ВМО ВСВ интервального НОУ:

При условии, что q₁= q₂= q₃= q₄= q₆= q₇=0, матрица состояния объекта принимает вид:

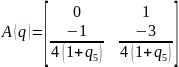
1. Назначим желаемую структуру собственных значений матрицы состояний F проектируемой системы в форме σ{F}={λ₁, λ₂=-15} где

2. Формирование матриц описания объекта

3. Формирование матрицы D

Так как , то матрицу вариаций можно представить как произведения столбца на строку:

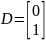
Определяем свободные параметры условия принадлежности:

(*)

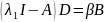
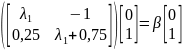
откуда следует что

Таким образом спектр собственных чисел матрицы F примет вид:

Проверка на принадлежность ядру матрицы:

Условие не выполняется, поэтому абсолютной параметрической инвариантности не достичь, и нужно ограничиться только некоторым значением ошибки по выходу в проектируемой системе.

4. Решение уравнений Сильвестра

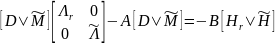
Представим это выражение в виде двух уравнений Сильвестра:

,

,

где

Найдем решение этих уравнений относительно матриц и 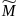соответственно:

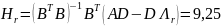
Вычислим матрицу отрицательной обратной связи :

5. Формирование матрицы прямой связи по задающему воздействию

Сконструируем матрицу 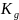прямой связи по внешнему задающему воздействию :

Построим реализационную версию закона управления в виде

,

где

Проверим эффективность спроектированного неадаптивного закона управления на предмет удовлетворения техническим требованиям показателей качества по выходу и ошибке номинальной версии системы, а также наличие у системы параметрической инвариантности. Промоделируем систему для вариаций параметра при угловых значениях

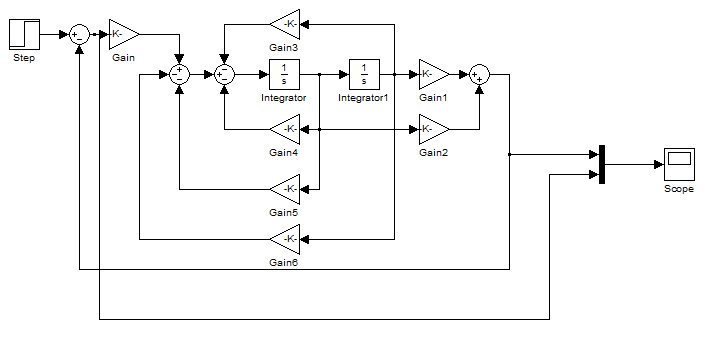
Рисунок 7.1. Схема моделирования спроектированной системы

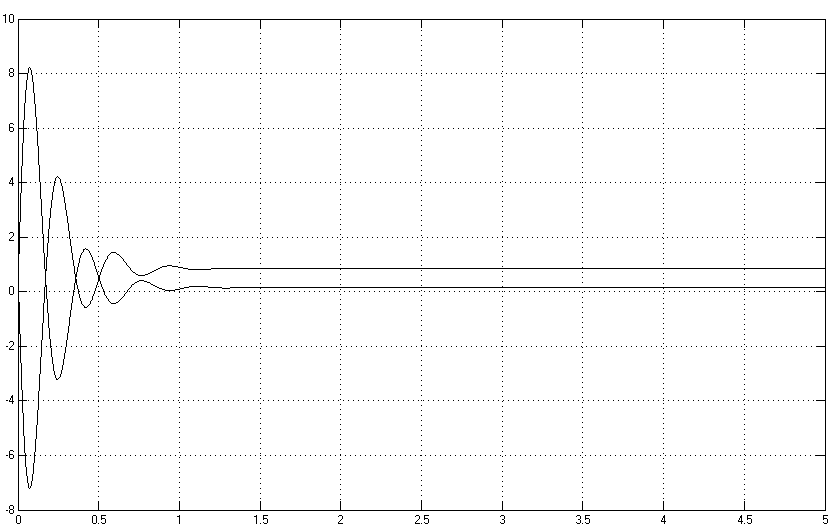
Рисунок 7.2. Графики переходных процессов

Для моего варианта расчетной условие не выполняется, поэтому абсолютной параметрической инвариантнотсти не достичь, и нужно ограничиться только некоторым значением ошибки по выходу в проектируемой системе.