
- •Задание 2 – Построение мтч доу к вариации интервала дискретности
- •3 Построение мтч дискретного объекта управления (доу) к вариации интервала дискретности
- •4 Построение матрицы функций модальной чувствительности, и выделение неблагоприятного сочетания вариаций параметров
- •5 Построение закона управления для объекта, заданного интервальными элементами
- •6 Исследование робастности полученной зс методом в.Л.Харитонова
- •7 Синтез параметрически инвариантной системы
- •8 Заключение
Санкт-Петербургский Государственный Университет
Информационных Технологий, Механики и Оптики
Кафедра Систем Управления и Информатики
Расчетная работа
по курсу «Адаптивные и робастные системы»
Вариант: А-А-А-А-Б-Б-Б-А
Выполнил:
студент группы 4148
Терегулов Б.З.
Проверила:
Слита О.В.
Санкт-Петербург
2011
Задание 1 – Построение МТЧ НОУ. Ранжирование параметров
Дана передаточная функция «вход-выход (ВВ)» НОУ:

где
 ,
,

 .
.
Передаточная функция вход-выход НОУ:

Перейдем к канонической управляемой форме:
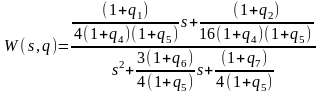
 - представление НОУ:
- представление НОУ:
 ,
,
 ,
,

Матрицы номинального ОУ:
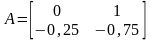 ,
,
 ,
,
 .
.
Построение семейства моделей траекторной чувствительности [1, 2]:

 ,
,
 ,
,
 ,
,
 .
.
Формирование семейства агрегированных систем:

где
 ,
,
 ,
,
 ,
,

Получим:
 ,
,
 ,
,
 ,
,

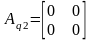 ,
,
 ,
,
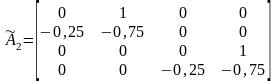 ,
,

 ,
,
 ,
,
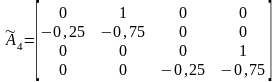 ,
,

 ,
,
 ,
,
 ,
,
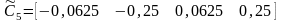
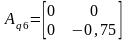 ,
,
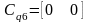 ,
,
 ,
,

 ,
,
 ,
,
 ,
,

Вычислим матрицы управляемости по функции траекторной чувствительности и их нормы:
 ,
,
 ,
,

 ,
,
 ,
,
 .
.
В силу неравенства:

проранжируем параметры по потенциальной чувствительности:
 .
.
В
результате проделанной работы делаем
вывод, что наибольшее влияние на вектор
выхода
 оказывает вариация параметра
оказывает вариация параметра
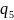 .
.
Задание 2 – Построение мтч доу к вариации интервала дискретности
Дан интервал дискретности
 ,
метод перехода к дискретному
векторно-матричному описанию ВСВ
описанию объекта управления (ДОУ) -
заменой производной отношением конечных
малых.
,
метод перехода к дискретному
векторно-матричному описанию ВСВ
описанию объекта управления (ДОУ) -
заменой производной отношением конечных
малых.

Переход к дискретному описанию ОУ осуществляется по формулам:
 ,
,
 ,
,
 ,
,
где
 ,
,

 ,
,
 ,
,
 ,
,
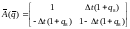 ,
,
откуда
при
 имеем:
имеем:
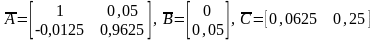 .
.
Построим модель траекторной чувствительности к вариации интервала дискретности:
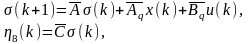
где
 ,
,
 ,
,
 ,
,
 .
.
Получим:
 ,
,

Построим агрегированный ОУ:
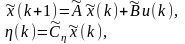
где
 ,
,
 ,
,
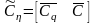
Получим:
 ,
,
 ,
,
 .
.
3 Построение мтч дискретного объекта управления (доу) к вариации интервала дискретности
Закон управления:
 должен доставлять системе
должен доставлять системе

где 
образованной объединением НОУ и ЗУ, с помощью:
матрицы
 прямой связи по входу
прямой связи по входу
 равенство входа
и выхода
равенство входа
и выхода
 в неподвижном состоянии при номинальных
значениях параметров;
в неподвижном состоянии при номинальных
значениях параметров;матрицы
 обратной связи по состоянию
обратной связи по состоянию

номинальных значений параметров распределение мод Баттерворта с характеристической частотой

Построить МТЧ спроектированной
системы по каждому из параметров и для
значения
 выделить доминирующие параметры по
степени их влияния на величину
выделить доминирующие параметры по
степени их влияния на величину
 перерегулирования и длительность
перерегулирования и длительность
 переходного процесса.
переходного процесса.
Оценить в процентах
отклонения величин перерегулирования
и времени переходного процесса систем
с неопределенностями от значений
![]() и
ЗС с номинальными параметрами (
и
ЗС с номинальными параметрами ( ).
).
По условию:
,
![]() ,
,

Из
требований к проектируемой системе
найдем матрицы
 :
:
Полином Баттерворта при заданной частоте:

отсюда:
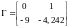
Матрица
 выбирается из условия полной наблюдаемости
пары
выбирается из условия полной наблюдаемости
пары
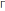 и
:
и
:
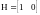
Решим
задачу медианного МУ с помощью уравнения
Сильвестра:


Найдем K:

Найдем
 :
:



Найдём :

Математическая версия закона управления:

Реализационная версия:
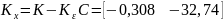

Замечание1.
Последняя версия будет реализуемой только в случае доступности измерению всех переменных состояния. В противном случае необходимо выстраивать наблюдатель с целью получения оценок переменных состояния. В этом случае закон управления примет вид:

где
 и
и
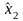 - оценки переменных состояния
- оценки переменных состояния
 и
и
 соответственно.
соответственно.
Найдем
 :
:

Замечание2.
При полученном желаемом
полиноме
 передаточная функция системы управления
примет вид:
передаточная функция системы управления
примет вид:

Переходная функция такой системы представлена на рисунке 3.1.

Рисунок 3.1 - Переходная функция СУ
Из рисунка видно, что перерегулирование превышает 550%. Это объясняется влиянием нуля передаточной функции. Тем не менее, формально требование об обеспечении распределения мод Баттерворта выполнено.
Построение семейства моделей траекторной чувствительности:

где  ,
,
 ,
, ,
,
и формирование семейства агрегированных систем:

где  ,
,
 ,
,
 ,
,

Получим:
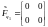 ,
,
 ,
,
 ,
,

 ,
,
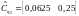 ,
,
 ,
,

 ,
,

 ,
,

 ,
,
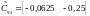
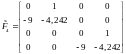 ,
,

 ,
,

 ,
,
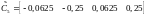
 ,
,
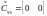
 ,
,

 ,
,
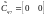
 ,
,

На рисунке 3.2. представлена структурная схема агрегированной системы: номинального объекта управления и модели траекторной чувствительности к вариации одного из параметров.

Рисунок 3.2 - Структурная схема агрегированной системы
Теперь представим графики
переходных функций номинальной системы
 в сравнении с параметрически возмущенной
в сравнении с параметрически возмущенной
 (по каждому из параметров).
(по каждому из параметров).

Рисунок
3.3 - Переходные функции агрегированной
системы при
 ,
,
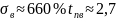 ,
,
 ,
,
 y=3.5
y=3.5

Рисунок
3.4 - Переходные функции агрегированной
системы при
 ,
,
 ,
,
 ,
y=3.6
,
y=3.6

Рисунок
3.5 -
Переходные функции агрегированной
системы при
 ,
,
 ,
,
y=0
,
,
y=0

Рисунок
3.6 - Переходные функции агрегированной
системы при
 ,
,
 ,
,
y=0,2
,
,
y=0,2

Рисунок
3.7 - Переходные функции агрегированной
системы при
 ,
,
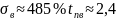 ,
,
y=1,6
,
,
y=1,6

Рисунок
3.8 - Переходные функции агрегированной
системы при
 ,
,
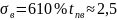 ,
,
y=1,8
,
,
y=1,8
Проанализируем полученные графики переходных функций возмущенных систем и проранжируем параметры по степени влияния на качество процессов:

Стоит отметить, что
вариация параметра
 оказывает наибольшее влияние, как на
перерегулирование, так и на время
переходного процесса (наибольшие
значения среди рассмотренных возмущенных
систем).
оказывает наибольшее влияние, как на
перерегулирование, так и на время
переходного процесса (наибольшие
значения среди рассмотренных возмущенных
систем).
