
- •2. Объектами гидромеханики являются капельные и упругие (газы) жидкости.
- •Глава I. Основы гидростатики
- •Глава 2. Основы гидродинамики
- •2.1. Основные уравнения кинематики и динамики невязкой жидкости
- •Уравнение неразрывности (сплошности, постоянства расхода)
- •3.2. Дифференциальные уравнения движения жидкости
- •Дифференциальные уравнения движения Навье-Стокса
- •Теорема жуковского о подъемной силе и направлении движения вихрей
- •Принцип подобия, как основа физического моделирования однофазных систем.
- •Закон сопротивления при движении однофазного потока
- •Основы теории гидравлических сопротивлений
- •2. Основное уравнение равномерного движения
- •3. Основной закон вязкого сопротивления
- •4. Касательное напряжение
- •5. Закон распределения скоростей при турбулентном движении.
- •Способы определения потерь напора при равномерном турбулентном движении
- •Местные сопротивления.
- •Лекция № 12 Истечение жидкости из отверстий
- •1. Истечение в атмосферу при постоянном напоре через малые отверстия в тонкой стенке
- •2. Истечение через большие отверстия в атмосферу.
- •3. Истечение через затопленное большое отверстие.
- •4. Истечение через насадки
- •8.1. Общие понятия
- •8.2. Основная формула расхода водослива
- •8.3. Водослив с острым порогом
- •8.3.1. Формы струй
- •8.3.2. Основные задачи гидравлического расчета
- •8.3.3 Определение коэффициента расхода
- •8.5. Водослив практического профиля
- •Лекция №14 Элементы реологии Течение неньютоновских жидкостей
- •Гидродинамика кипящих (псевдоожиженных) зернистых слоев
- •Механизм переноса вещества и законы диффузии
- •1. Основные понятия и определения
- •Критерии подобия процессов массопередачи в однофазном потоке
- •Основы теории турбулентного массопереноса в процессах обогащения (сепарации).
- •Уравнение (1.24) принимает вид
- •Давление частиц рв на эту пластинку сверху равно
- •Соответственно извлечение частиц этого сорта составит:
- •Гидроциклоны – аппараты, использующие вихревые турбулентные потоки для разделения минералов по плотности и классификации их по крупности.
2. Истечение через большие отверстия в атмосферу.
Основной задачей при истечении через большие отверстия в атмосферу является определение расхода. Реверсия в атмосферу является определение
 расхода.
Решить эту задачу так, как она была
решена для малого отверстия, оказывается
затруднитель-ным, так как скорости в
сжатом сечении не равны друг другу и
распределение скоростей происходит по
некоторому сложному закону (рис. 6).
расхода.
Решить эту задачу так, как она была
решена для малого отверстия, оказывается
затруднитель-ным, так как скорости в
сжатом сечении не равны друг другу и
распределение скоростей происходит по
некоторому сложному закону (рис. 6).
Наиболее просто задача решается следующим образом.
Всегда можно записать, что расход, проходящий через данное отверстие любой формы и размера, определяется по формуле
где
![]() –
площадь сжатого сечения, а
–
площадь сжатого сечения, а
![]() – средняя скорость в этом сечении. При
этом всегда
,
а
– средняя скорость в этом сечении. При
этом всегда
,
а
![]() (здесь
Н – напор в центре тяжести площади
отверстии).
(здесь
Н – напор в центре тяжести площади
отверстии).
Тогда
![]() ,
,
или,
обозначив
![]() буквой m,
расход через любой отверстие можно
определить по формуле
буквой m,
расход через любой отверстие можно
определить по формуле
![]() . (9)
. (9)
Здесь m
- коэффициент расхода,
его значения заключены в широких
пределах, в зависимости от условий входа
![]() до
0,95.
до
0,95.
Можно, конечно, определить расход и по уравнению
![]() .
.
Если отверстие
прямоугольное и расположено в вертикальной
стенке, то для элементарной площадки
![]() расход
можно определять по формуле расхода
для малых отверстий
расход
можно определять по формуле расхода
для малых отверстий
![]() .
.
Тогда для всего отверстия расход определим путем интегрирования
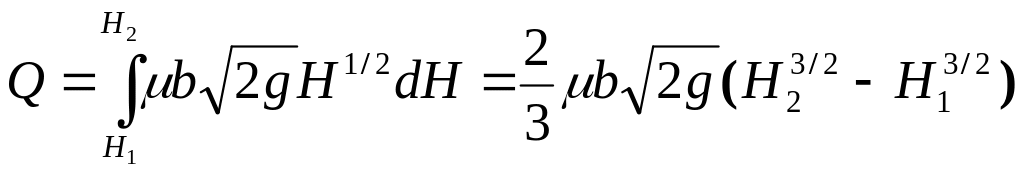
или
![]() .
(9а)
.
(9а)
Этот прием
определения расхода возможен, но он,
очевидно, не представляет собой строгого
решения, так как здесь при интегрировании
принимается
![]() ,
что не отвечает действительности
,
что не отвечает действительности
На
практике часто принимают
![]() (как
для малых круглых отверстий) тогда
(как
для малых круглых отверстий) тогда
![]() .
.
3. Истечение через затопленное большое отверстие.
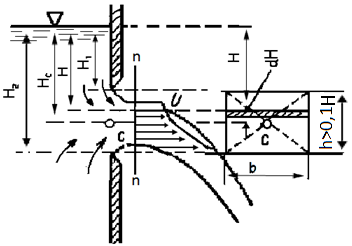
Опыт показывает, что при малом заглублении отверстия свободная поверхность снижается как перед отверстием, так и непосредственно за ним (рис. 7.7) В результате возникает прорыв воздуха через отверстие (“захлебывание” отверстия) и нарушается стационарность движения.
Здесь будем рассматривать истечение только при достаточно большом заглублении, когда указанным явлением можно пренебречь.
Определим скорость в сжатом сечении. Выбрав сечение 1-1 и сечение n-n (рис. 7.7), напишем (для точек 1 и 2)
![]() .
.
Здесь
![]() -скорость
подхода, определенная как
-скорость
подхода, определенная как
![]() ;
;
![]() - скорость в избранной точке сжатого
сечения;
- скорость в избранной точке сжатого
сечения;
![]() -
коэффициент Кориолиса;
- коэффициент сопротивления;
-
коэффициент Кориолиса;
- коэффициент сопротивления;
![]() - площадь сечения 1-1.
- площадь сечения 1-1.
Из
этого уравнения, обозначив
![]() и приняв
,
найдем скорость истечения
и приняв
,
найдем скорость истечения
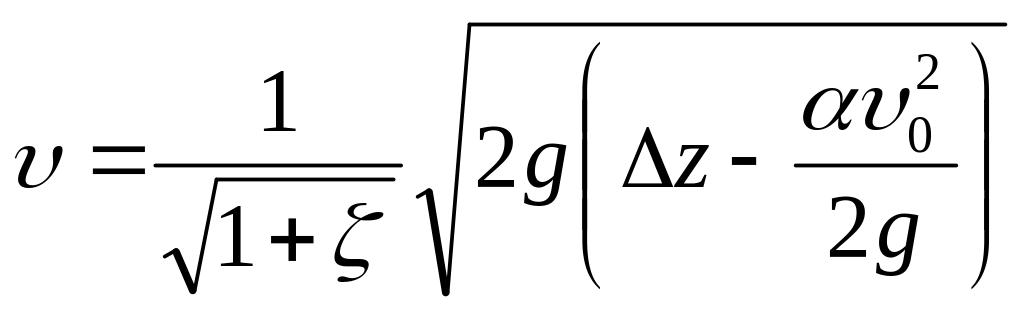
или, обозначив, как обычно, , получим
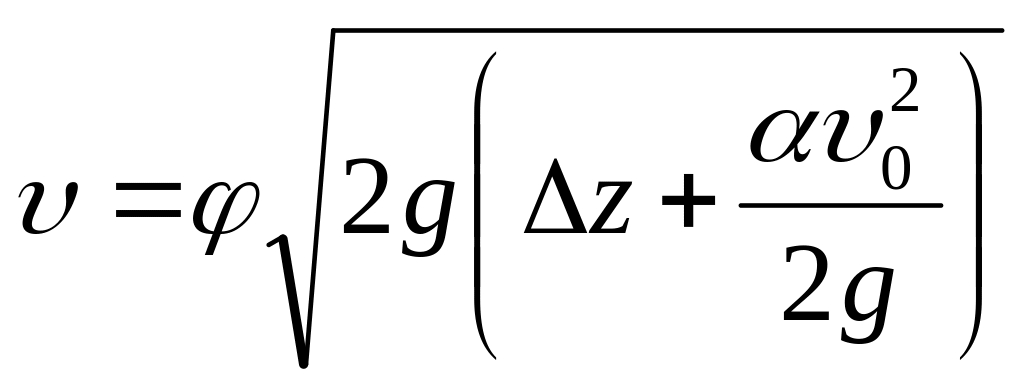 .
(10)
.
(10)
Нетрудно видеть, что полученная формула аналогична формуле (4) при истечении в атмосферу.
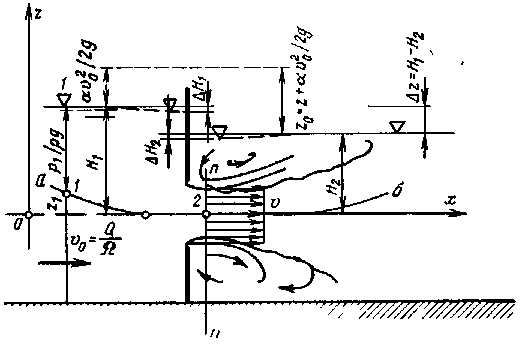
Рис. 7.
Расход, проходящий через затопленное отверстие, получим по формуле
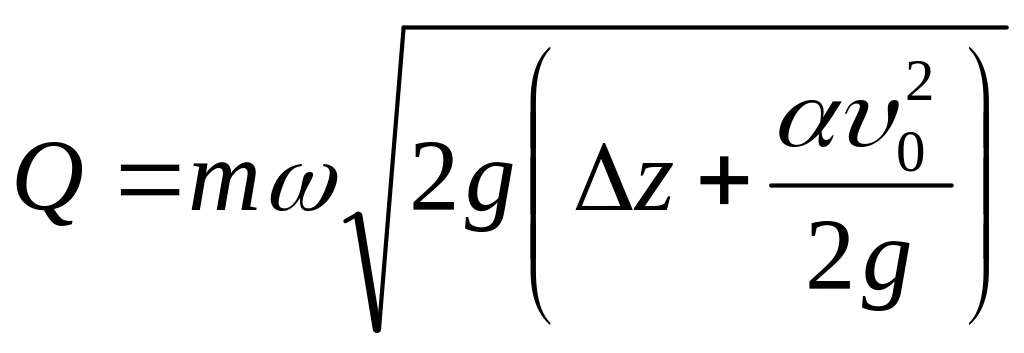 .
.
