4. Касательное напряжение

Процесс перемешивания вызывает перенос количест­ва движения из области малых скоростей потока в об­ласть больших скоростей и обратно. Очевидно, массы с малыми скоростями при входе в область течений с большими скоростями будут тормозить движение в этой области, т. е. оказывать силовое противодейст­вие движению. Это будут силы инерции, и, следовательно, физическая природа тур­булентных сопротивлений — инерционная. Массы жидко­сти с большими скоростя­ми, оказывая давление на присоединенные массы, уско­ряют их движение и расхо­дуют при этом свою энергию (при этом ускорении возни­кают сил и инерции).

О пределим касательные напряжения. Рас­смотрим два слоя: слой а—а и слой b-b (рис. 12). Пусть слом а-а движется со скоростью, равной про­екции полной скорости частицы и на ось 0-х (u_х=u∙cosα), а слой b—b движется со скоростью u_x+du_x. При этом за время dt из слоя а—а в слой b—b через площадку dω=dx dy, параллельную координатной пло­скости х0у, проходит масса dm=ρdx dyu_zdt и внедряется в слой b—b, приобретая там скорость u_x+du_x.

Составим уравнение изменения количества движения для массы dm:

(28)

Здесь dF — сила, действующая на массу dm в тече­ние времени dt, представляющая собой воздействие жидкости за пределами слоя a—а на массу dm в про­цессе ее перемещения в слой b—b.

С учетом равенства dm=ρdx dyu_zdt получим

Сила F направлена параллельно оси Ох и приходится на площадь dω=dxdy, поэтому касательное напряже­ние τ для площадки ω равно:

(29)

После подстановки и сокращения на dt получим

откуда

(30)

Здесь скорость , но осредненная скорость , так как расход потока направлен вдоль оси трубы, т. е. вдоль оси Ох, а вдоль оси Оz равен нулю (препятствуют жесткие стенки самой трубы). Поэтому . Примем далее условие , что возмож­но допустить, выбирая соответственно расстояние меж­ду слоями а-a и b-b.

Итак, для касательного напряжения можно записать:

(31)

Это будет мгновенное касательное напря­жение, а осредненное касательное напря­жение т определится по известной формуле осред­нения

(32)

Здесь, очевидно, усредняется значение подынтеграль­ной функции , и таким образом будем иметь выра­жение осредненного касательного напряжения

(33)

5. Закон распределения скоростей при турбулентном движении.

Рис.13

Прандтль при установлении закона распределения скоростей принял следующую схему течения в трубопроводе.

У стенок трубы скорости принимаются нулевыми, к центру (оси трубы) они постепенно увеличиваются, т.е. у стенок трубы создается ламинарный слой небольшой толщины δ, за пределами которого располагается центральная основная часть потока – турбулентное ядро. В связи с малыми скоростями течения в ламинарном (пристенном) слое скорости быстро нарастают, градиент скорости велик, и его можно приближенно считать величиной постоянной. В пределах центрального ядра турбулентное течение и изменение скоростей происходят не так интенсивно. Иллюстрация такой схемы показана на рис. 13.

Будем рассматривать закон распределения осредненных скоростей в центральном турбулентном ядре.

Для установления этого закона надо иметь зависимость касательного напряжения от градиента скорости (так же как и при решении этого вопроса при ламинарном движении), т.е. . Тогда, интегрируя такое дифференциальное уравнения, получаем искомую зависимость

Воспользуемся формулой (33). Входящие в нее пульсационные компоненты и по физической природе зависят от градиента скорости du_x/dz, но такая зависимость неизвестна. Поэтому введем гипотезу

и ,

где коэффициенты k₁ и k₂ должны иметь линейную размерность

Тогда из (33) после подстановки получим:

Произведение двух коэффициентов k₁, k₂ можно заменить одним множителем и написать:

,

где l, так же как и коэффициенты k₁ и k₂ имеет линейную размерность:

(34)

Эта формула принадлежит Прандтлю.

Введенный множитель l Прандтль назвал длиной пути перемешивания, понимая этот путь как расстояние, проходимое частицей с начальной скоростью для приобретения скорости того слоя с координатой z, в который внедряется эта частица.

Касательное напряжение , определяемое (34), не зависит от вязкости, но в реальных условиях при неравномерном распределении скоростей в поперечном сечении (т.е. при наличии градиентов скорости) возникает и вязкостное касательное напряжение (как и при ламинарном движении) и, следовательно, результативно полное касательное напряжение

.

Эту формулу можно записать иначе:

. (35)

Легко видеть, что выражение 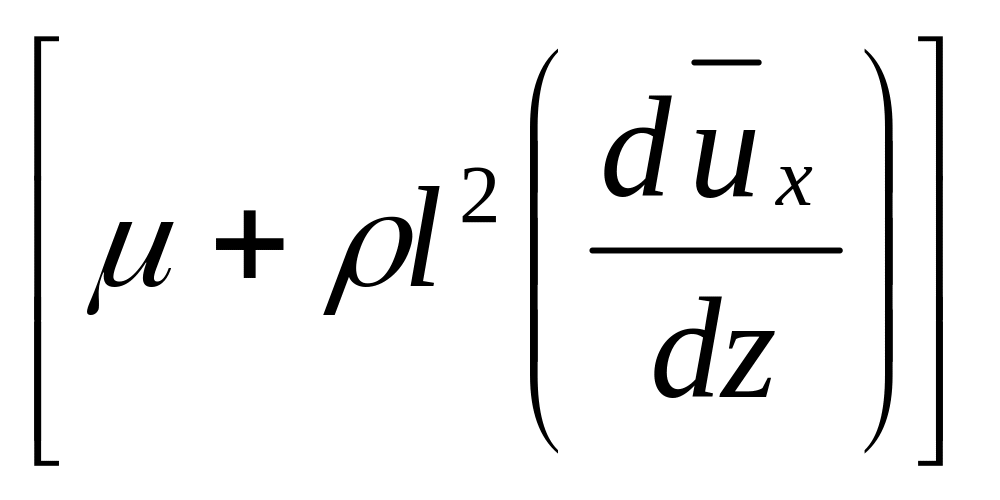играет роль вязкости турбулентного потока (подобно вязкости для ламинарных потоков), тогда, обозначив

,

можно записать:

. (36)

Уравнение (36) ( - вязкость при турбулентном движении) было предложено Буссинеском в 70-х годах прошлого века без теоретического обоснования, а по аналогии с законом Ньютона .

При больших числах Re вдали от стенок касательное напряжение зависит в основном от турбулентного состояния потока ( ) и наоборот.

Рассмотрим распределение скоростей в условиях, когда можно пренебречь , т.е. касательным напряжение вязкости.

Извлекая квадратный корень из уравнения (34) и решая относительно получаем:

.

Для интегрирования этого уравнения Прандтль ограничивает пределы интегрирования пространством от ламинарного пристенного слоя внутрь турбулентного ядра, принимая и линейную зависимость l от координаты z в виде

, (37)

где коэффициент и называется по Прандтлю универсальной постоянной, а - касательное напряжение на стенке, определяемое по (7). ПО опытам Никурадзе .

После подстановки получим дифференциальное уравнение

, (38)

где

Интегрируя (38) находим:

. (39)

Итак, распределение скорости по нормали к стенке трубы подчиняется логарифмическому закону.

Поскольку величина выражается в м/с, т.е. единице скорости, Прандтль ввел понятие скорость касательного напряжения, обозначив её u_*

(40)

Эту скорость в отечественной литературе обычно именуют динамической скоростью (по М. Н. Великанову).

Пользуясь основным уравнением равномерного движения (7), можем определять u_*, м/с, иначе:

(40а)

Используя понятие динамической скорости, (39) запишем проще:

. (41)

Определим значение постоянной С.

Значение постоянной интегрирования С находим по граничным условиям. Для турбулентного ядра имеем две границы: первая – наружная поверхность перехода ламинарного течения у стенки в турбулентный, отстоящая от оси трубы на расстоянии , и вторая – внутренняя , также цилиндрическая, вырождающаяся с приближением к центру в осевую линию трубопровода. На оси имеет место максимальная скорость , а на границе ламинарного слоя

В соответствии с этим получи на оси и , и тогда

.

Определив отсюда С, получим (41) в таком виде:

.

Для построения эпюры скоростей по этому уравнению надо иметь в виду, что координата z лежит в пределах

,

где - толщина пристенного ламинарного слоя (ламинарной пленки).

Определим толщину ламинарной пленки .

Известно, что или , но и .

Поэтому

или .

По опытным данным , сходная по структуре с числом Re, равна 11,6. Обозначив , найдем толщину пленки

. (43)

Очевидно тогда, что .

Из (43) видно, что толщина ламинарного слоя уменьшается с увеличением гидравлического уклона, а так как число при этом возрастает, то толщина δ убывает с увеличением Re.

Среднюю скорость определим по формуле .

Расход

.

Скорость можно определить по (42), так как z=r₀-r, то

.

Элементарная площадка сечении трубы

.

Итак, расход

.

Интегрируя, получаем:

.

Тогда средняя скорость

(44)

Обозначив 3/(2x)=D, получим из (5.44)

(44а)

или

(45)

По своему физическому смыслу D представляет недостачу средней скорости до максимальной (определенной в безразмерной форме), поэтому эта величина и получила название дефицит скорости. Опыты показывают, что дефицит скорости оказывается мало изменяемой величиной, и её можно считать постоянной, что и надо было ожидать, так как D зависит только от универсальной постоянной Прандтля x. Если принять x=0,40, то для дефицита скорости D получим:

.

Примечание. Многочисленные опыты показали, что универсальная постоянная Прандтля x колеблется приблизительно в пределах

0,3<x<0,45,

а дефицит скорости в пределах

3,3<D<4.

Потерянный напор в трубах определяется по формуле Дарси-Вейсбаха

.

Входящий в эту формулу коэффициент сопротивления λ при ламинарном движении (24) равен 64/Re, т.е. зависит только от числа Рейнольдса.

При турбулентном движении он зависит от многих факторов, при этом зависимость от числа Рейнольдса оказывается более сложной.

Вводя в формулу Дарси-Вейсбаха взамен диаметра d гидравлический радиус R (равный R=d/4) и учитывая известное соотношение , можем записать

,

а так как , то

или после извлечения квадратного корня

.

С учетом формулы (5.44а) можно записать и так:

. (46)

Но поскольку неизвестно отношение для вычисления λ по этой формуле, произведем некоторые преобразования. Из формулы (5.42) имеем:

. (47)

Здесь, как известно, .

Определим отношение :

но так как , то

.

Тогда (47) можно записать так:

(48)

С учетом (48) перепишем формулу (5.46) в таком виде (переходя к десятичным логарифмам):

(49)

или в самой общей форме (формула Прандтля)

. (49а)

Здесь числовые значения А и В зависят от принятого значения x, при x=0,4 получим:

.

На основе экспериментальных исследований Никурадзе формула Прандтля получила окончательный вид:

. (50)

при x=0,45

.

На основании опытных данных получена более удобная формула (формула Конакова):

рис. 14 (51)

Формула Прандтля (50) получена теоретическим путем в предположении, что толщина пристенного ламинарного слоя δ больше высоты выступов шероховатости ε (рис. 14), благодаря чему пристенный слой как бы устраняет влияние выступов на развитие водоворотных образований турбулентного потока. Однако во многих случаях это условие не соблюдается. Толщина пристенного слоя δ уменьшается с увеличением числа Re, поэтому в одной и той же трубе с данной неизменной шероховатостью, но с увеличением расхода Q, а следовательно, с увеличением Re наступает нарушение условия и шероховатость начинает оказывать свое влияние. При очень больших числах Re шероховатость играет большую и даже решающую роль.