
- •Глава 7. Линейные операторы в евклидовом пространстве
- •§1. Некоторые сведения о матрицах
- •Ортогональные и унитарные матрицы
- •Свойства ортогональных и унитарных матриц
- •Некоторые свойства эрмитовых и симметричных матриц
- •§ 2. Сопряженный линейный оператор
- •Свойства сопряженных операторов
- •§ 3. Самосопряженные линейные операторы
- •§4. Приведение уравнений кривых и поверхностей
- •Если обозначить
- •§ 5. Изометрии
- •§ 6. Классификация линейных операторов на евклидовой
- •Плоскости и в трехмерном евклидовом пространстве
- •Ортогональные операторы на евклидовой плоскости
- •Ортогональные операторы в трехмерном евклидовом пространстве
- •Симметричные операторы в
- •Разложение произвольного линейного оператора в действительном евклидовом пространстве в произведение симметричного и ортогонального
- •§ 7. Одновременное приведение к каноническому виду пары квадратичных форм
- •Правило приведения пары квадратичных форм к каноническому виду
Правило приведения пары квадратичных форм к каноническому виду
Пусть и – квадратичные формы на действительном линейном пространстве , причем положительно определена. Выберем в какой-либо базис
, (7.28)
и
обозначим
и
![]() матрицы форм
и
соответственно в этом базисе. В
пространстве
скалярное произведение зададим с помощью
симметричной билинейной формы,
соответствующей квадратичной форме
.
Это значит, линейное пространство
превращается в евклидово
матрицы форм
и
соответственно в этом базисе. В
пространстве
скалярное произведение зададим с помощью
симметричной билинейной формы,
соответствующей квадратичной форме
.
Это значит, линейное пространство
превращается в евклидово
![]() ,
а матрица Грама базиса (7.28) совпадает с
.
Как и во всяком евклидовом пространстве,
в
существует ортонормированный базис
,
а матрица Грама базиса (7.28) совпадает с
.
Как и во всяком евклидовом пространстве,
в
существует ортонормированный базис
. (7.29)
Если
![]() –
матрица Грама базиса (7.28), а
–
матрица квадратичной формы
в этом базисе, то
–
матрица Грама базиса (7.28), а
–
матрица квадратичной формы
в этом базисе, то
![]() ,
,
![]() .
В силу ортонормированности базиса
(7.29)
.
В силу ортонормированности базиса
(7.29)
![]() ,
значит,
,
значит,
![]() ,
откуда получаем, что
,
откуда получаем, что
![]() .
.
Согласно теореме 7.7, в существует ортонормированный базис, в котором квадратичная форма имеет канонический вид. Чтобы найти этот канонический вид, следует решить характеристическое уравнение
![]() (7.30)
(7.30)
а
чтобы найти векторы искомого базиса,
следует для каждого собственного
значения
![]() решить систему линейных уравнений
решить систему линейных уравнений
![]() ,
(7.31)
,
(7.31)
где
![]() –
координатный столбец искомого собственного
вектора в базисе (7.29). Но
–
координатный столбец искомого собственного
вектора в базисе (7.29). Но
{(7.30)}
{![]() }
{
}
{![]() }
}
{![]() },
},
откуда вытекает, что (7.30) равносильно уравнению
![]() .
(7.32)
.
(7.32)
Система
же (7.31) преобразуется так: {(7.31)}
{![]() }
}
{![]() }
{
}
{![]() }.
Если
}.
Если
![]() – координатный столбец искомого
собственного вектора в базисе (7.28), то
– координатный столбец искомого
собственного вектора в базисе (7.28), то
![]() ,
значит, система (7.31) равносильна следующей:
,
значит, система (7.31) равносильна следующей:
![]() .
(7.33)
.
(7.33)
Таким образом, диагональные элементы матрицы – это корни уравнения (7.32), а векторы искомого базиса – это решения системы линейных уравнений (7.33) для каждого из найденных значений .
Из вышесказанного получаем следующее правило одновременного приведения пары квадратичных форм к каноническому виду:
1. Выписываем матрицы квадратичных форм и определяем, какая из них положительно определена. Матрицу положительно определенной квадратичной формы обозначаем , а оставшуюся – .
2. Составляем уравнение (7.32), которое также называется характеристическим, и находим его корни . Записываем канонический вид каждой из квадратичных форм: будет иметь нормальный вид, а коэффициенты канонического вида формы совпадают с найденными собственными значениями .
3. Находим ортогональный базис, решая систему линейных уравнений (7.33) при каждом из найденных собственных значений .
4. Нормируем каждый вектор (скалярное произведение задано формой !).
5. Составляем
матрицу перехода от исходного базиса
к ортонормированному базису из собственных
векторов и по ней записываем линейное
невырожденное преобразование переменных
![]() .
.
Пример. Приведем одновременно к каноническому виду квадратичные формы
![]() и
и
![]() .
.
▼1. Записываем матрицы обеих квадратичных форм:
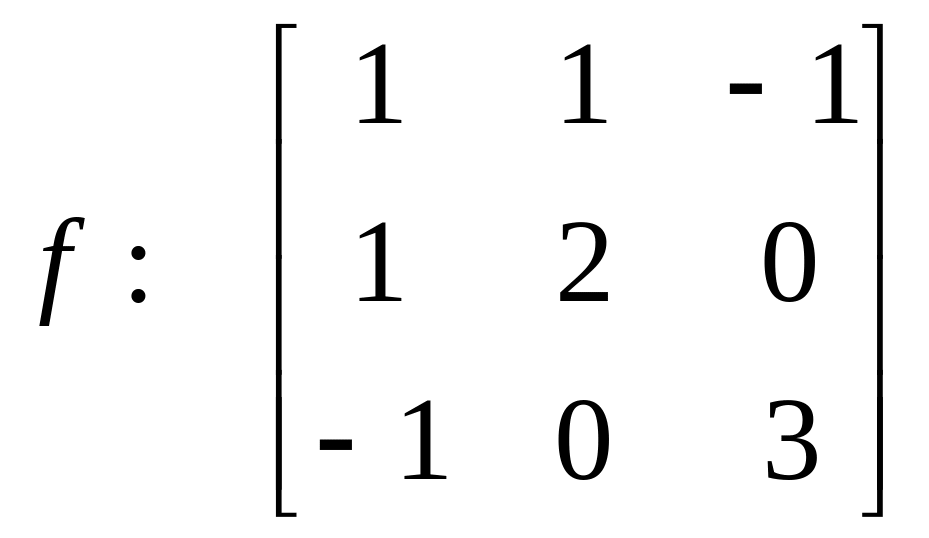 ,
,
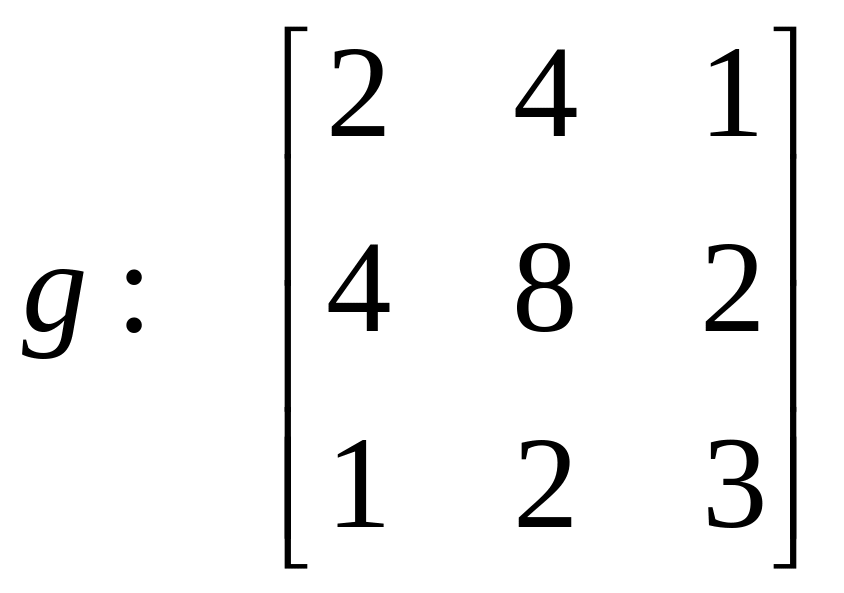 .
.
Исследуем
на знакоопределенность форму
по критерию Сильвестра:
![]() .
Итак, положительно определена форма
.
Значит,
.
Итак, положительно определена форма
.
Значит,
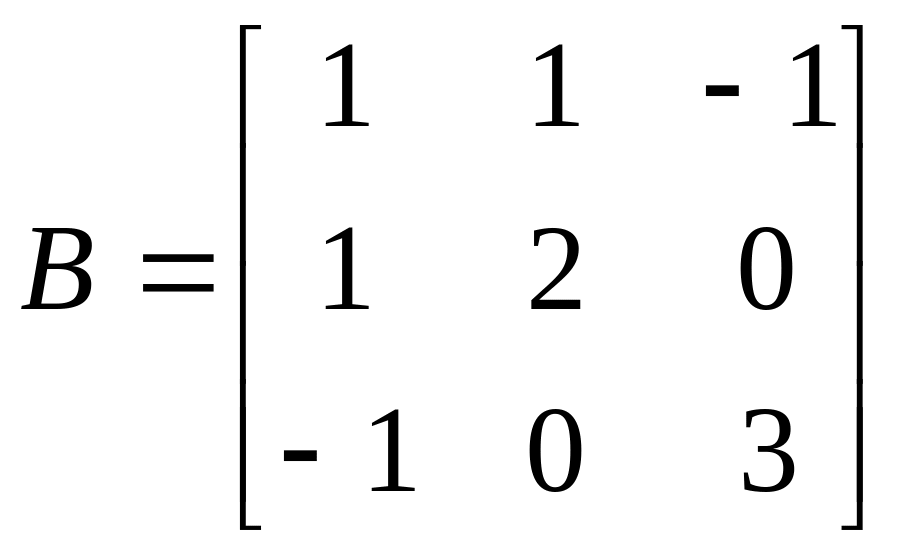 ,
,
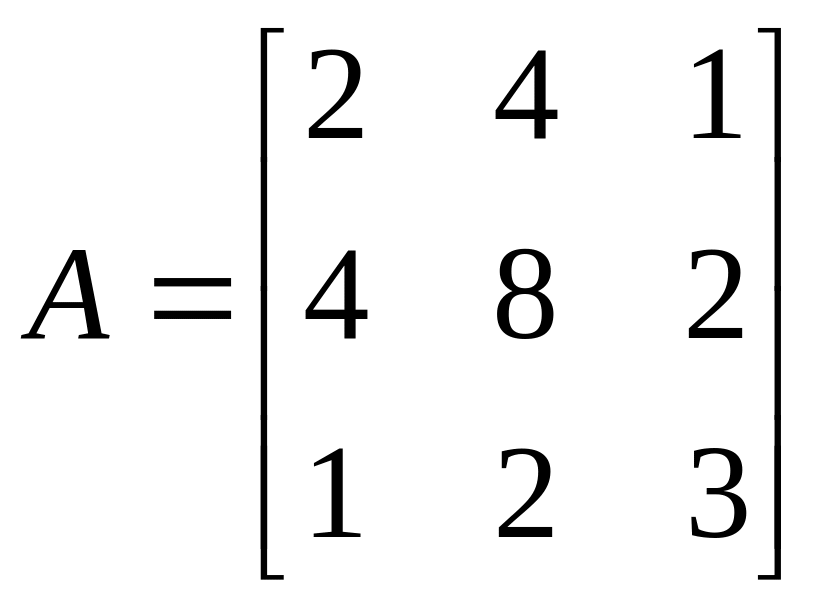 .
.
2.

![]() .
.
Записываем
характеристическое уравнение
![]() и находим его корни:
и находим его корни:
![]()
Канонический
вид квадратичной формы
![]() ,
а формы
,
а формы
![]() .
.
3.
![]() :
:

![]()
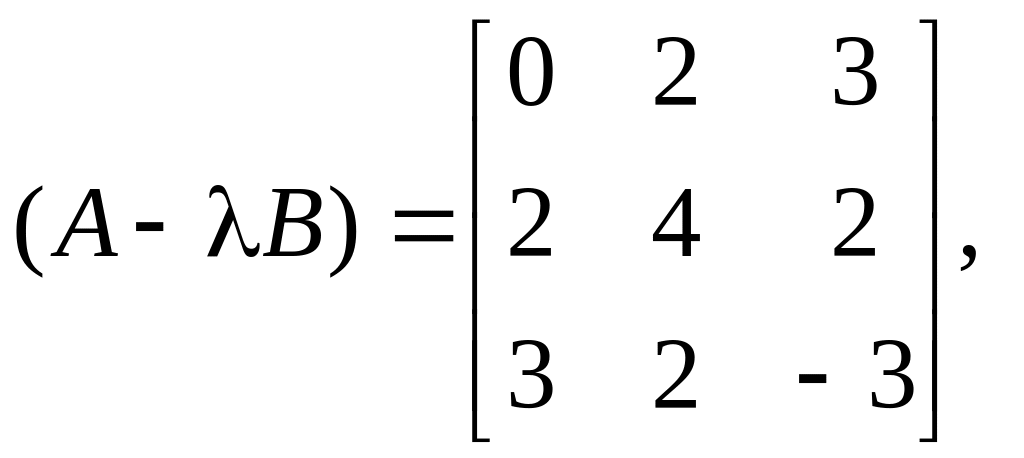
![]()

![]()
![]()
![]()
4.
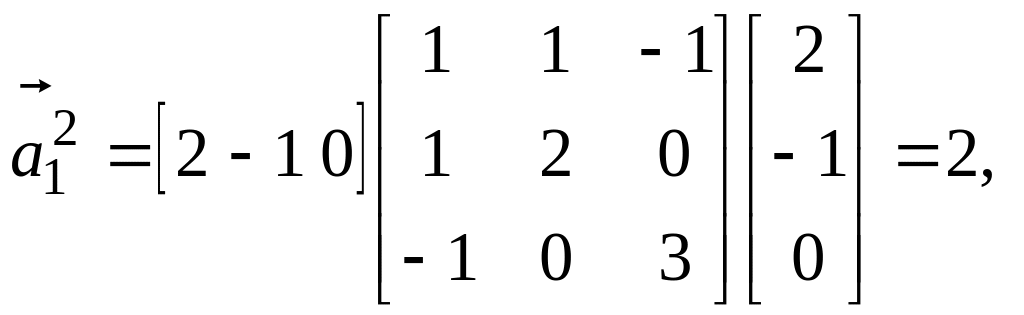
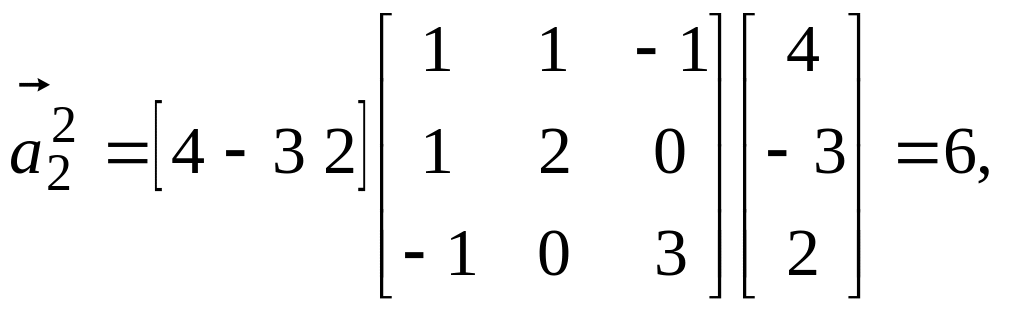

![]()
![]()
![]()
5.
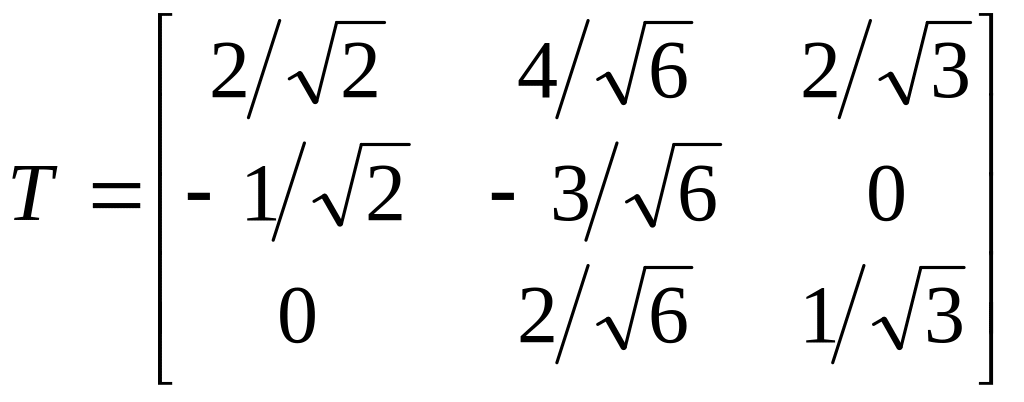 ;
;
![]()
