Симметричные операторы в

Как было доказано в § 3, для любого симметричного оператора в существует ортонормированный базис, в котором матрица оператора имеет диагональный вид. Перечислим все принципиально возможные различные случаи.

– тождественный оператор;

– симметрия относительно оси;

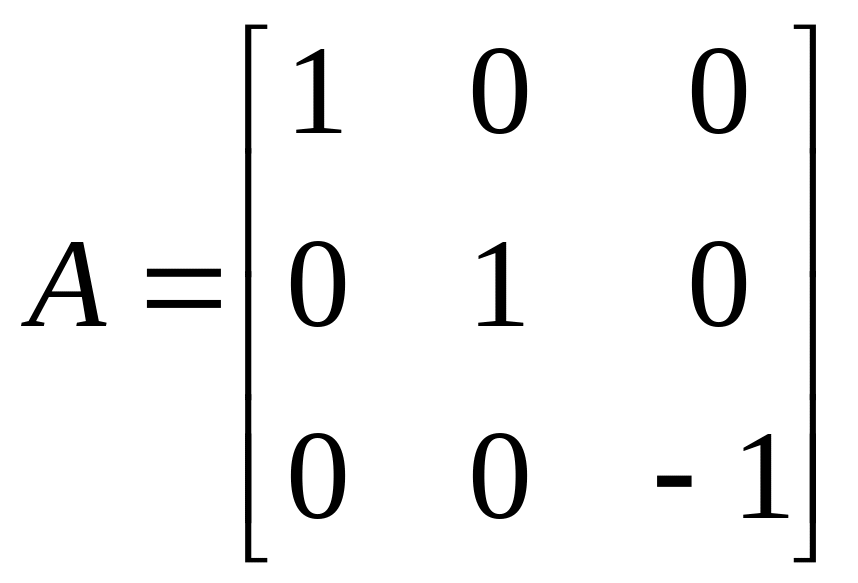– симметрия относительно плоскости;

– симметрия относительно начала координат;

(перечисленные операторы одновременно являются и ортогональными);

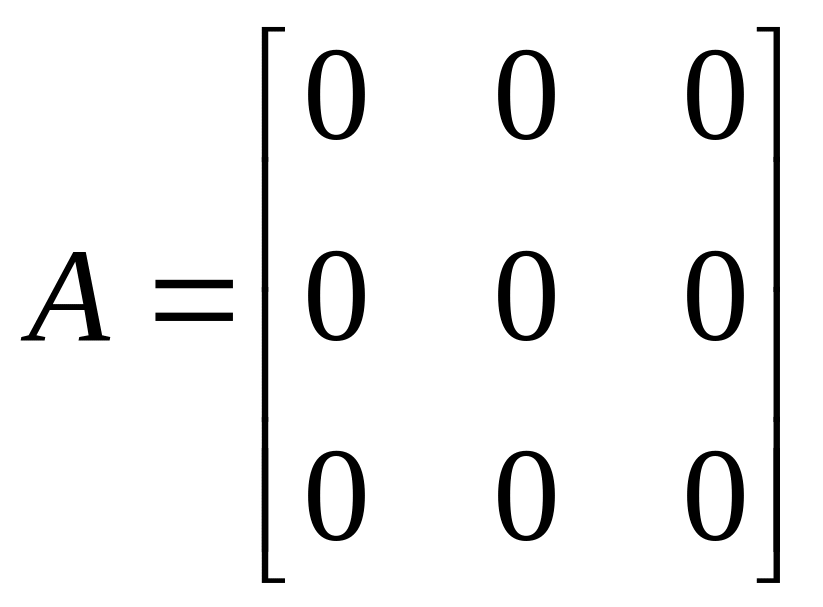– нулевой оператор;

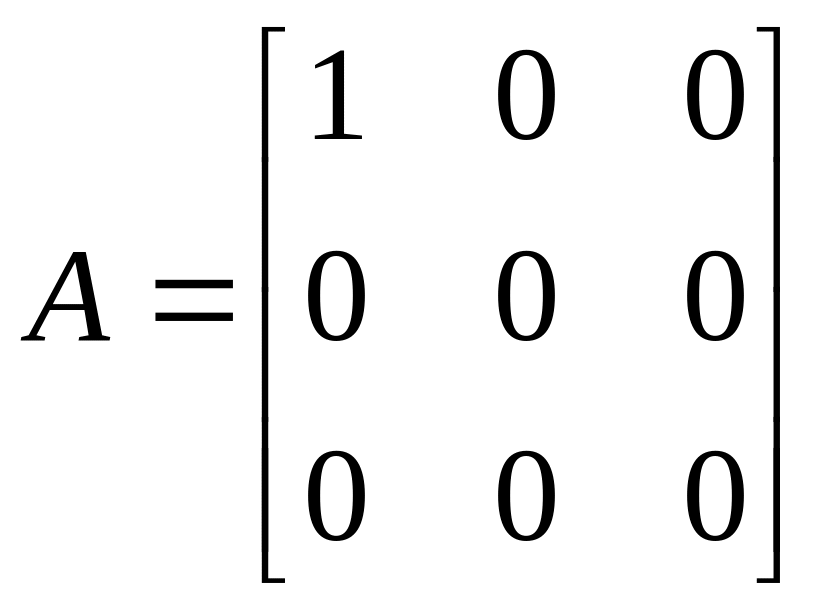– проектирование на ось с направлением вектора ;

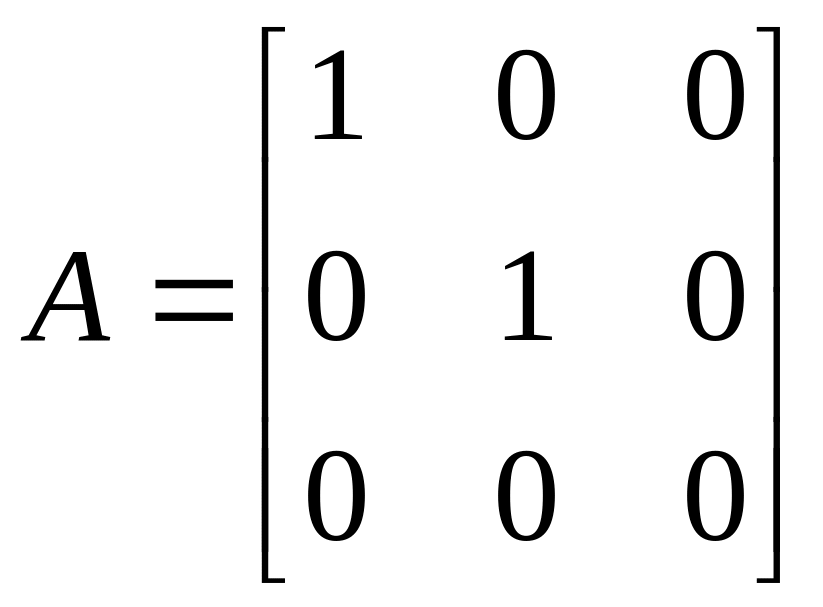– проектирование на плоскость, перпендикулярную вектору ;

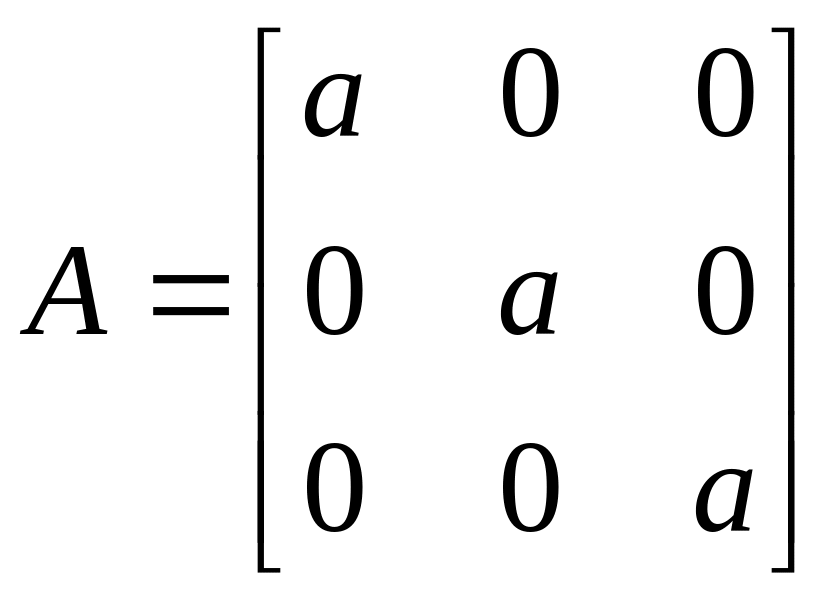– растяжение при и сжатие при ;

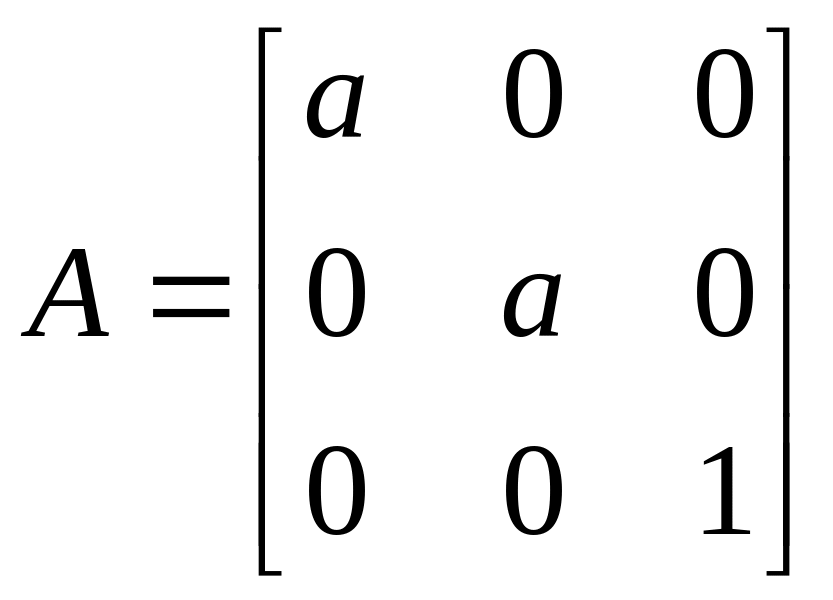– растяжение от оси при и сжатие к оси при ;

– растяжение вдоль оси при и сжатие вдоль оси при

.

Рассмотрим теперь некоторую диагональную матрицу

,

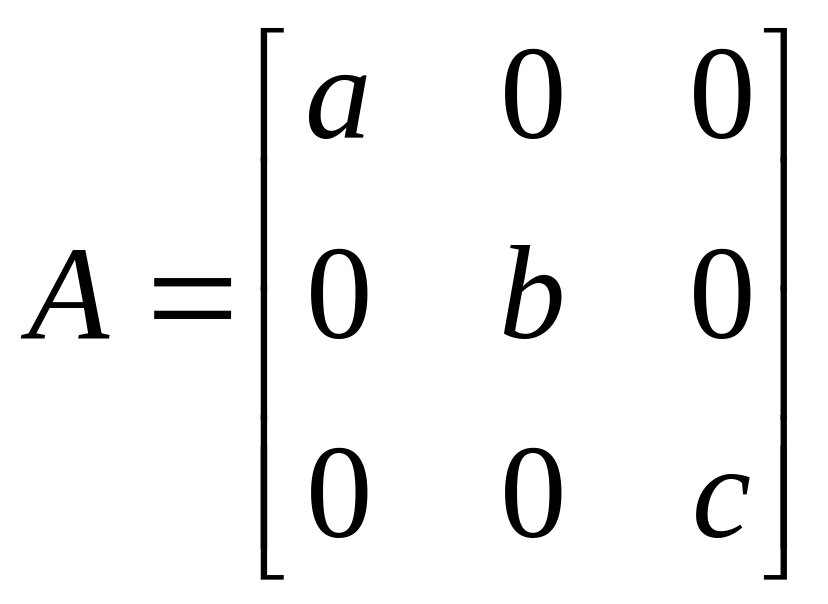в которой, например, . Тогда

,

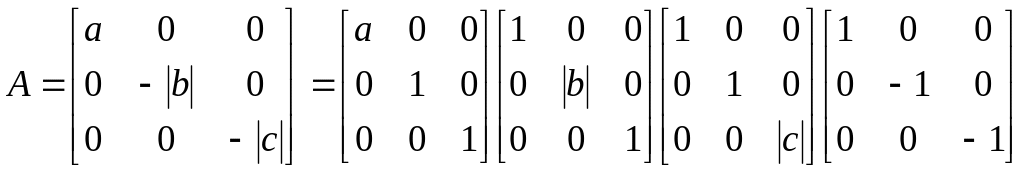т. е. оператор, заданный матрицей , есть композиция растяжений (или сжатий) вдоль трех взаимно перпендикулярных осей и симметрии относительно оси. Любая диагональная матрица может быть представлена в виде произведения перечисленных выше десяти простейших матриц. Например, при положительных и

,

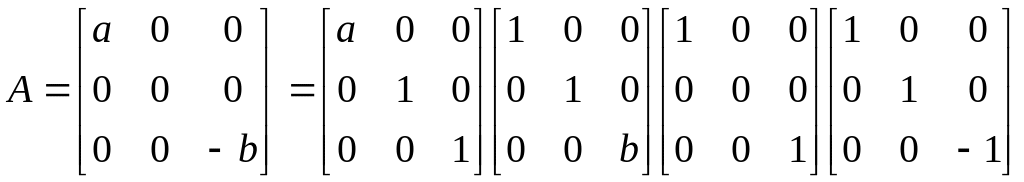откуда вытекает, что оператор с такой матрицей есть композиция двух растяжений вдоль осей, проектирования на плоскость и симметрии относительно другой плоскости.

Разложение произвольного линейного оператора в действительном евклидовом пространстве в произведение симметричного и ортогонального

Теорема 7.14. Пусть – действительное евклидово пространство. Для любого невырожденного линейного оператора существуют симметричный и ортогональный операторы такие, что .

►Рассмотрим линейный оператор . Так как , то оператор симметричный. Если – собственное значение оператора , а – соответствующий ему собственный вектор, то . С другой стороны, . Итак, , откуда вытекает, что . На самом деле, в силу невырожденности , . Как и для любого симметричного оператора, для в существует ортонормированный базис

, (7.25)

в котором матрица оператора имеет диагональный вид

,

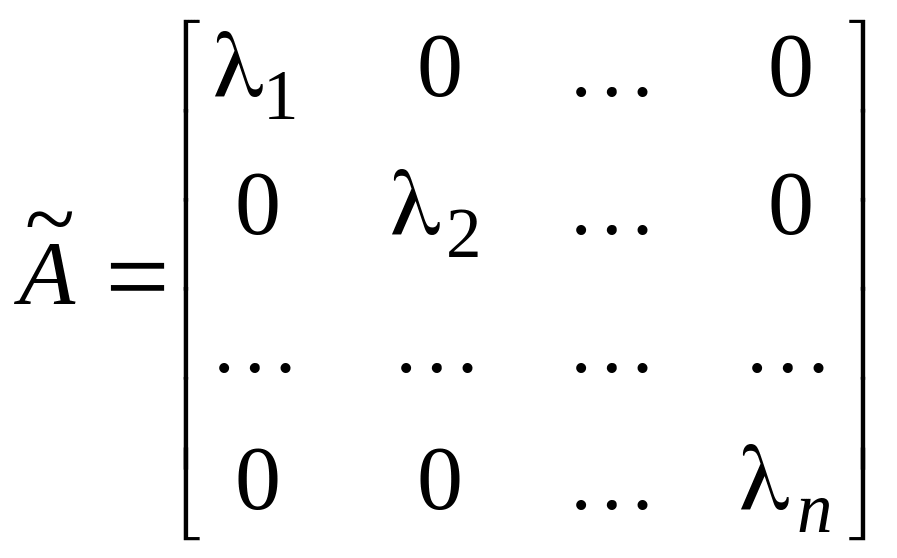причем , и не обязательно различные. Обозначим тот линейный оператор, который в базисе (7.25) имеет матрицу

.

Так как , то . Очевидно, оператор – симметричный и невырожденный, поэтому существует обратный ему линейный оператор , также симметричный (его матрица в базисе (7.25) – это

,

она тоже симметрична). Положим

. (7.26)

Учитывая, что [симметрия ] = , делаем вывод, что – ортогональный оператор. Теперь из (7.26) получаем . ◄

Можно доказать, что эта теорема справедлива и для вырожденных линейных операторов.

Следствие. Любая действительная квадратная матрица может быть представлена в виде произведения ортогональной и симметричной матриц.

§ 7. Одновременное приведение к каноническому виду пары квадратичных форм

Теорема 7.15. Пусть и – квадратичные формы на действительном линейном пространстве , причем одна из них положительно определена. Тогда в существует базис, в котором обе квадратичные формы имеют канонический вид.

►Пусть, например, квадратичная форма положительно определена. Тогда соответствующая ей симметричная билинейная форма тоже положительно определена. С помощью этой билинейной формы можно задать скалярное произведение на линейном пространстве и после этого оно превращается в евклидово пространство . Согласно теореме 7.7, в существует ортонормированный базис

, (7.27)

в котором форма имеет канонический вид. Так как базис (7.27) ортонормированный, то . Значит, квадратичная форма в базисе (7.27) имеет единичную матрицу, и поэтому форма в этом базисе имеет нормальный вид. ◄