
- •Глава 7. Линейные операторы в евклидовом пространстве
- •§1. Некоторые сведения о матрицах
- •Ортогональные и унитарные матрицы
- •Свойства ортогональных и унитарных матриц
- •Некоторые свойства эрмитовых и симметричных матриц
- •§ 2. Сопряженный линейный оператор
- •Свойства сопряженных операторов
- •§ 3. Самосопряженные линейные операторы
- •§4. Приведение уравнений кривых и поверхностей
- •Если обозначить
- •§ 5. Изометрии
- •§ 6. Классификация линейных операторов на евклидовой
- •Плоскости и в трехмерном евклидовом пространстве
- •Ортогональные операторы на евклидовой плоскости
- •Ортогональные операторы в трехмерном евклидовом пространстве
- •Симметричные операторы в
- •Разложение произвольного линейного оператора в действительном евклидовом пространстве в произведение симметричного и ортогонального
- •§ 7. Одновременное приведение к каноническому виду пары квадратичных форм
- •Правило приведения пары квадратичных форм к каноническому виду
§ 6. Классификация линейных операторов на евклидовой
Плоскости и в трехмерном евклидовом пространстве
Ортогональные операторы на евклидовой плоскости
Выберем
на евклидовой плоскости
![]() какой-либо ортонормированный базис
какой-либо ортонормированный базис
![]() .
Если А
– матрица ортогонального оператора
.
Если А
– матрица ортогонального оператора
![]() в этом базисе, то она ортогональна.
Значит,
в этом базисе, то она ортогональна.
Значит,
![]() .
Найдем характеристический многочлен
матрицы А:
.
Найдем характеристический многочлен
матрицы А:
![]() .
.
Рассмотрим сначала случай, когда
![]() .
Тогда характеристическое уравнение
имеет вид
.
Тогда характеристическое уравнение
имеет вид
![]() .
Это уравнение имеет два различных
действительных корня. Значит, ортогональный
оператор
имеет два различных собственных значения:
.
Это уравнение имеет два различных
действительных корня. Значит, ортогональный
оператор
имеет два различных собственных значения:
![]() и
и
![]() .
В таком случае в
существует ортонормированный базис
.
В таком случае в
существует ортонормированный базис
![]() ,
состоящий из собственных векторов
оператора
,
в котором матрица
,
состоящий из собственных векторов
оператора
,
в котором матрица
![]() оператора
имеет диагональный вид:
оператора
имеет диагональный вид:
![]() .
.
Линейный
оператор с этой матрицей, как мы знаем,
есть не что иное, как оператор симметрии
относительно оси, направление которой
задается вектором
![]() .
.
Пусть теперь
![]() .
Определим в этом случае элементы матрицы
А, учитывая, что она ортогональная,
т. е. что
.
Определим в этом случае элементы матрицы
А, учитывая, что она ортогональная,
т. е. что
![]() .
Пусть
.
Пусть
![]() .
.
Тогда
![]() ,
,
откуда получаем систему для определения элементов матрицы:
![]() (7.24)
(7.24)
Из первых
двух уравнений системы (7.24) видно, что
можно положить
![]() ,
где
,
где
![]() и
и
![]() – некоторые углы, причем
– некоторые углы, причем
![]() (так как нам важно знать не сами углы, а
значения их синусов и косинусов).
Последние два уравнения этой системы
определяют соотношения между углами
и
:
(так как нам важно знать не сами углы, а
значения их синусов и косинусов).
Последние два уравнения этой системы
определяют соотношения между углами
и
:
![]() .
.
Значит, матрица А выглядит так:
![]() .
.
Как мы уже
знаем, это матрица оператора поворота
плоскости на угол
вокруг начала координат. В частности,
если
![]() ,
то
,
то
![]() ,
т. е. получаем тождественный оператор.
Если же
,
т. е. получаем тождественный оператор.
Если же
![]() ,
то
,
то
![]() .
Этой матрице соответствует оператор
симметрии относительно начала координат.
.
Этой матрице соответствует оператор
симметрии относительно начала координат.
Таким образом, ортогональные операторы на евклидовой плоскости – это тождественный оператор, симметрия относительно начала координат или относительно некоторой оси, либо поворот плоскости вокруг начала координат.
Ортогональные операторы в трехмерном евклидовом пространстве
Известно, что всякий многочлен третьей
степени с действительными коэффициентами
имеет, по крайней мере, один действительный
корень. Поэтому всякий линейный, в том
числе и ортогональный оператор
![]() имеет, по крайней мере, одно собственное
значение
имеет, по крайней мере, одно собственное
значение
![]() ,
причем
,
причем
![]() .
Пусть
.
Пусть
![]() – единичный собственный вектор
ортогонального оператора
– единичный собственный вектор
ортогонального оператора
![]() с собственным значением
.
Обозначим
с собственным значением
.
Обозначим
![]() и рассмотрим
и рассмотрим
![]() .
Очевидно,
– двумерное евклидово пространство.
Выберем произвольные векторы
.
Очевидно,
– двумерное евклидово пространство.
Выберем произвольные векторы
![]() и
и
![]() .
Тогда
.
Тогда
![]() – собственный
– собственный![]() ортогональность
ортогональность
![]()
![]() .
.
Обозначим
![]() такой линейный оператор, что
такой линейный оператор, что
![]()
(![]() отличается от
только областью определения). Очевидно,
– тоже ортогональный оператор. Как и в
любом евклидовом пространстве, в
пространстве
можно выбрать ортонормированный базис
отличается от
только областью определения). Очевидно,
– тоже ортогональный оператор. Как и в
любом евклидовом пространстве, в
пространстве
можно выбрать ортонормированный базис
![]() .
Тогда
.
Тогда
![]() – ортонормированный базис пространства
– ортонормированный базис пространства
![]() .
Матрица оператора
в этом базисе имеет блочно диагональный
вид
.
Матрица оператора
в этом базисе имеет блочно диагональный
вид
![]() ,
,
где
![]() – матрица оператора
в базисе
.
В силу того, что оператор
ортогональный, матрица
тоже ортогональная. Это значит, что в
подходящем ортонормированном базисе
она может быть одной из матриц:
– матрица оператора
в базисе
.
В силу того, что оператор
ортогональный, матрица
тоже ортогональная. Это значит, что в
подходящем ортонормированном базисе
она может быть одной из матриц:
![]() .
.
Перечисляя всевозможные принципиально различные виды матриц в подходящем ортонормированном базисе пространства , получаем
а)
![]() .
.
 ,
– тождественный оператор;
,
– тождественный оператор;
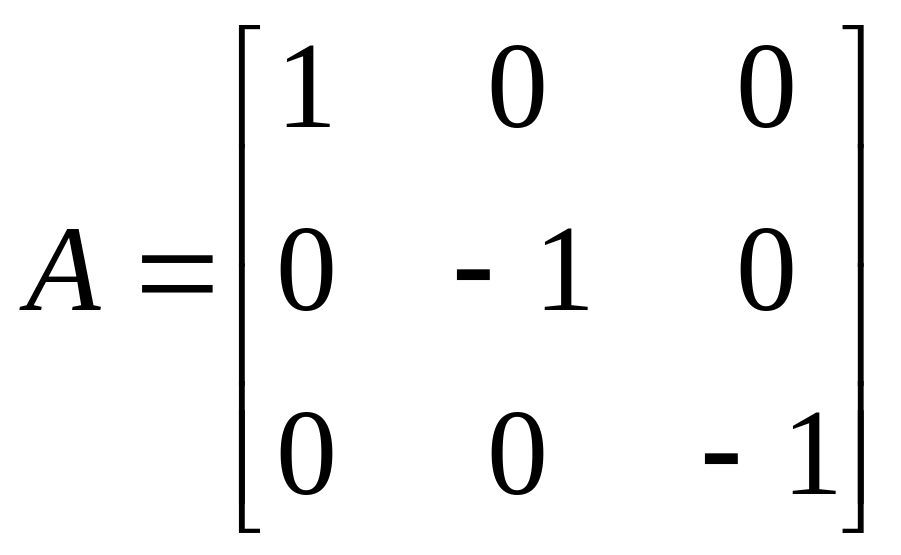 ,
– симметрия относительно оси с
направлением вектора
;
,
– симметрия относительно оси с
направлением вектора
;
 ,
– симметрия относительно плоскости,
перпендикулярной вектору
,
– симметрия относительно плоскости,
перпендикулярной вектору
![]() ;
;
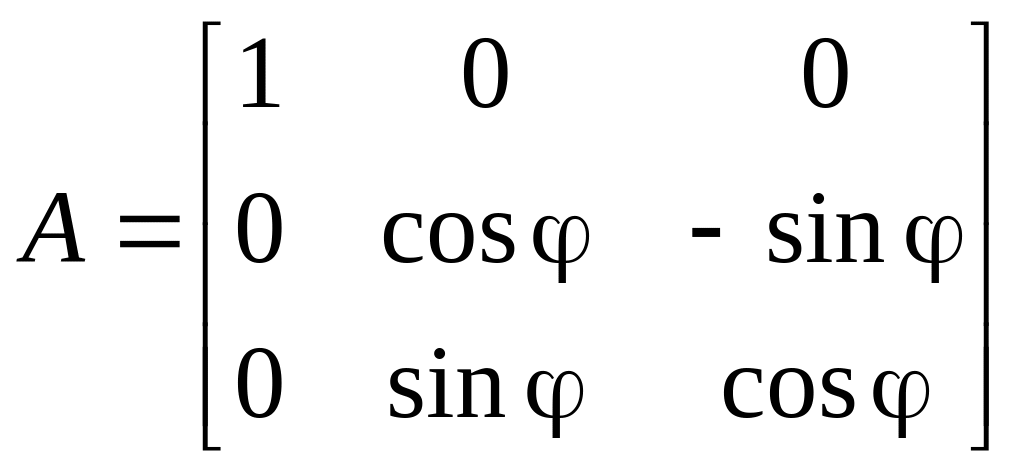 ,
– поворот вокруг оси с направлением
вектора
.
,
– поворот вокруг оси с направлением
вектора
.
б)
![]() .
.
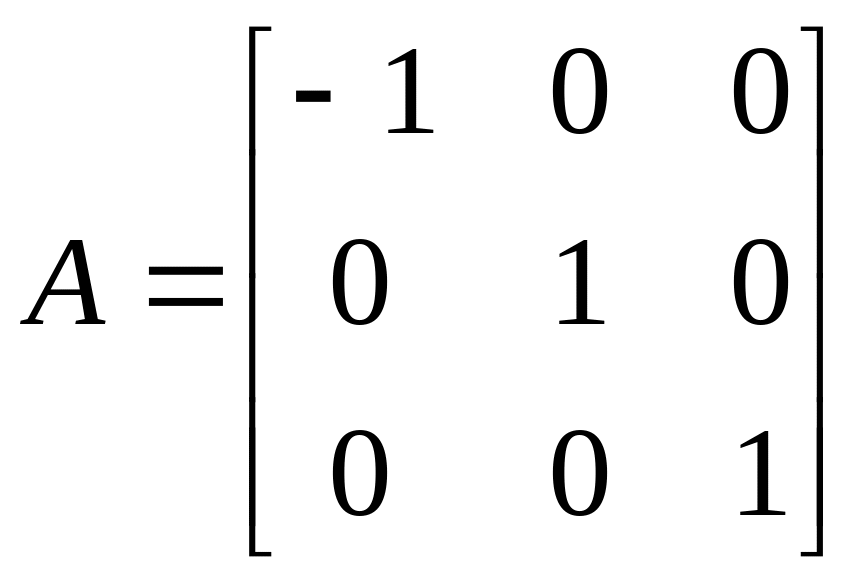 ,
– симметрия относительно плоскости,
перпендикулярной вектору
;
,
– симметрия относительно плоскости,
перпендикулярной вектору
;
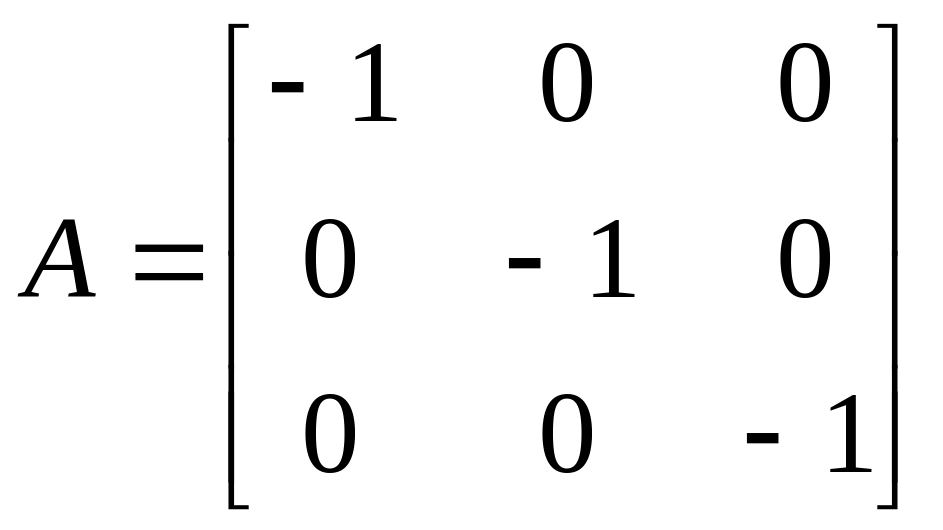 ,
– симметрия относительно начала
координат;
,
– симметрия относительно начала
координат;
 ,
– симметрия относительно оси с
направлением вектора
,
– симметрия относительно оси с
направлением вектора
![]() ;
;
 ,
– композиция поворота вокруг оси с
направлением вектора
и симметрии относительно плоскости,
перпендикулярной этому же вектору.
,
– композиция поворота вокруг оси с
направлением вектора
и симметрии относительно плоскости,
перпендикулярной этому же вектору.
Таким образом, все ортогональные операторы в трехмерном евклидовом пространстве – это: тождественный; симметрия относительно плоскости; симметрия относительно оси; симметрия относительно начала координат; поворот вокруг оси и композиция поворота вокруг оси и симметрии относительно плоскости, перпендикулярной этой же оси.
