§4. Приведение уравнений кривых и поверхностей

второго порядка к каноническому виду

Теорема 7.7. Для любой квадратичной формы на действительном евклидовом пространстве в этом пространстве существует ортонормированный базис, в котором рассматриваемая квадратичная форма имеет канонический вид.

► Пусть на евклидовом пространстве задана квадратичная форма k. Выберем в какой-либо ортонормированный базис

, (7.7)

и пусть А – матрица квадратичной формы k в этом базисе. Тогда А – симметричная, а значит, существует такая ортогональная матрица Т, что матрица – диагональная. Так как матрица Т ортогональная, то по теореме 7.1 в существует ортонормированный базис

(7.8)

такой, что Т – матрица перехода от (7.7) к (7.8). Если Ã – матрица квадратичной формы k в базисе (7.8), то = = = = А'. Матрица А' – диагональная и поэтому в базисе (7.8) квадратичная форма k имеет канонический вид.◄

Замечание. Диагональными элементами матрицы А' являются собственные значения матрицы А.

Определение. Линейное невырожденное преобразование переменных называется ортогональным, если его матрица ортогональна.

Теорема 7.8. Любую действительную квадратичную форму можно привести к каноническому виду при помощи ортогонального преобразования переменных (иная формулировка теоремы 7.7).

Следствия. 1. Для того чтобы действительная квадратичная форма была положительно определенной необходимо и достаточно, чтобы все собственные значения ее матрицы были положительными.

2. Для любой поверхности второго порядка в трехмерном пространстве существует ортонормированная система координат, в которой эта поверхность задается каноническим уравнением.

Для любой кривой второго порядка на плоскости существует ортонормированная система координат, в которой эта кривая задается каноническим уравнением.

Пример. Определить вид кривой второго порядка, приведя ее уравнение к каноническому виду, и нарисовать эту кривую, если исходное уравнение кривой имеет вид

.

▼1. Приводим к каноническому виду квадратичную часть уравнения (т. е. квадратичную форму) с помощью ортогонального преобразования переменных. Для этого записываем матрицу этой квадратичной формы и находим ее собственные значения:

, , .

Для нахождения первого собственного вектора решаем систему линейных уравнений с матрицей при : , . Чтобы найти второй собственный вектор нет необходимости решать вторую систему. Достаточно вспомнить, что он ортогонален вектору в силу симметричности матрицы А и что его координаты можно получить, как и в аналитической геометрии, переставив местами координаты вектора и в одной из них поменяв знак. Итак, . Чтобы получить ортонормированный базис, векторы и нормируем, т.е. делим каждый на его длину: , . Канонический вид квадратичной формы выглядит так: . Матрица перехода (она же матрица линейного невырожденного преобразования переменных) имеет вид

.

2. По матрице T записываем линейное невырожденное преобразование переменных:

(7.9)

Подставляем выражение переменных по формулам (7.9) в исходное уравнение. При этом квадратичная часть переходит в известный нам канонический вид, свободный член не меняется, а чтобы узнать, как изменится линейная часть, следует непосредственно подставить формулы (7.9) в уравнение, раскрыть скобки и привести подобные.

Замечание. На самом деле коэффициенты линейной части есть линейные комбинации координат векторов и с теми же коэффициентами, что и в исходном уравнении. Например, коэффициент при вычисляется так: , а при – так: .

Таким образом, после преобразования (7.9) приходим к уравнению

,

которое равносильно следующему:

.

3. Преобразуем это уравнение:

и применим к нему преобразование параллельного переноса:

После этого уравнение кривой принимает вид

,

откуда видно, что исследуемая кривая – парабола.

4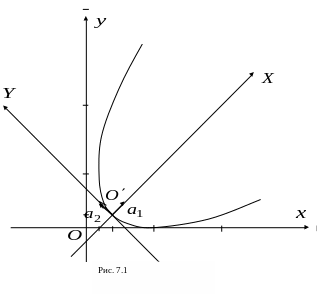 . Приступаем к рисованию. На одном рисунке изображаем и старую систему координат, и новую. При преобразовании параллельного переноса начало координат переходит в точку , в которой . Значит, . Можно узнать координаты точки и в исходной системе координат. Для этого значения и подставим в формулы (7.9): . Итак, . Направление новых осей удобнее определять не по векторам и , а по векторам и , так как они имеют целочисленные координаты (рис. 7.1).

Как видите, приведение к каноническому виду даже кривой второго порядка – занятие достаточно трудоемкое. Попробуем его упростить хотя бы в некоторых случаях.

Лемма 7.2. Для того чтобы начало координат было центром симметрии кривой второго порядка, необходимо и достаточно, чтобы коэффициенты при первых степенях переменных в ее уравнении равнялись нулю.

►Обозначим рассматриваемую кривую второго порядка. Пусть ее уравнение имеет вид:

. (7.10)

Необходимость.

{О – центр симметрии кривой Ф}

. (7.11)

Рассмотрим два случая.

а) Кривая Ф не является сдвоенной прямой. Тогда на ней можно выбрать две точки и , не лежащие с началом координат на одной прямой. Из (7.11) получаем

(7.12)

причем . Поэтому система (7.12) имеет единственное решение .

б) Ф – сдвоенная прямая . Очевидно, утверждение истинно.

Достаточность очевидна, так как уравнение кривой Ф имеет вид

.◄

Обозначим левую часть уравнения (7.10). Тогда

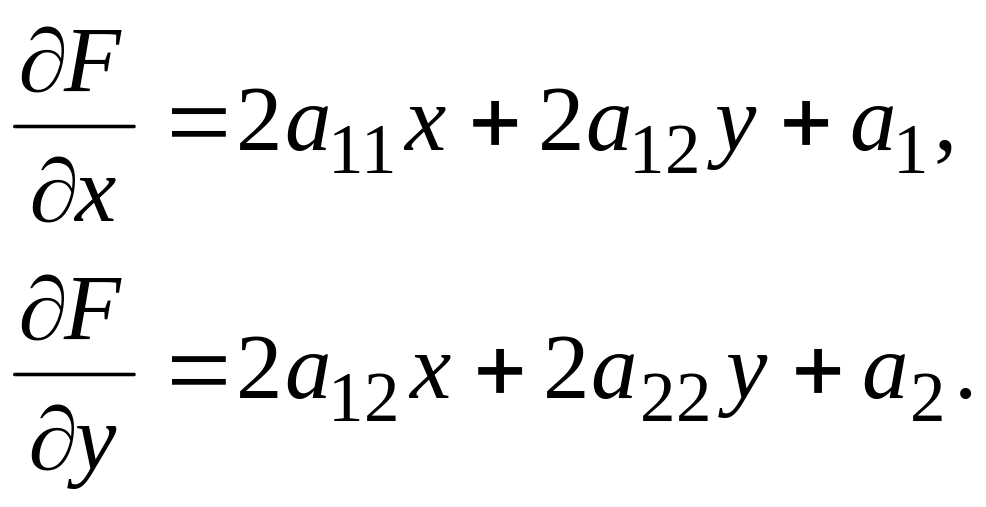(7.13)

Теорема 7.9. Для того чтобы точка была центром симметрии кривой второго порядка , необходимо и достаточно, чтобы координаты этой точки удовлетворяли системе линейных уравнений

(7.14)

►Пусть – центр симметрии кривой Ф с уравнением (7.10). Применим преобразование параллельного переноса , которое помещает начало координат в точку . При этом преобразовании уравнение (7.10) изменится так:

Последнее уравнение равносильно следующему:

. (7.15)