4. Расчет механических систем, приведение действующих нагрузок к валу электродвигателя. Приведение моментов сопротивления к валу электродвигателя.

В большинстве ЭМС электродвигатель приводит в действие производственный механизм через систему передач, элементы которой могут осуществлять как вращательные так и поступательные движения, с момент сопротивления приложенный к производственному механизму.

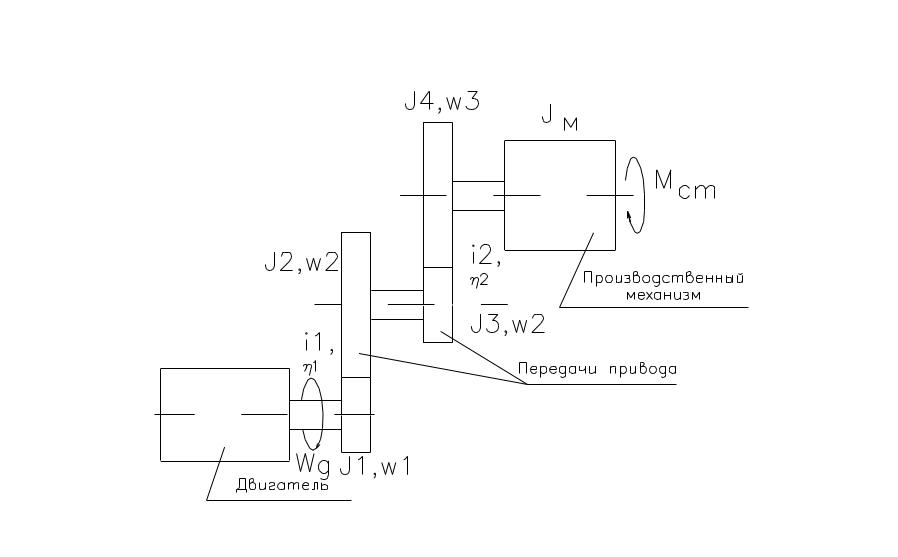
Рис.1

В процессе приведения необходимо определить такой момент М_с, который приложен к валу двигателя оказывает на систему такое же действие как и момент М_см, приложенный к производственному механизму этот момент и называется приведенным.

Приведение моментов сопротивления выполняется на основании уравнения энергетического баланса: мощность, передаваемая всем элементам системы, с учетом КПД, остается неизменной.

, где

- КПД всего механизма

Приведение Сил сопротивления к валу электродвигателя.

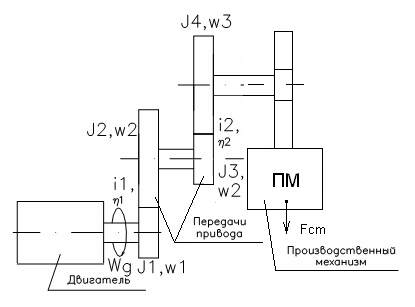
Рис. 2

Для приведения вращательного движения в поступательное уравнение записывается в виде:

Fc – приведенная сила

Uд – скорость выходного элемента двигателя

Приведение моментов инерции и масс к валу двигателя.

Привеление моментов инерции к валу двигателя осуществляется на том основании, что запас кинематической энергии, отнесенный к одной оси, остается неизменным.

Ii – момент инерции передач системы

Im – момент инерции производственного механизма

Целью приведения является нахождении такого момента инерции, который будучи соединенным с валом двигателя, оказывает на системы такое же действие как и различные элементы системы вращающиеся с различной скоростью.

- для поступательного

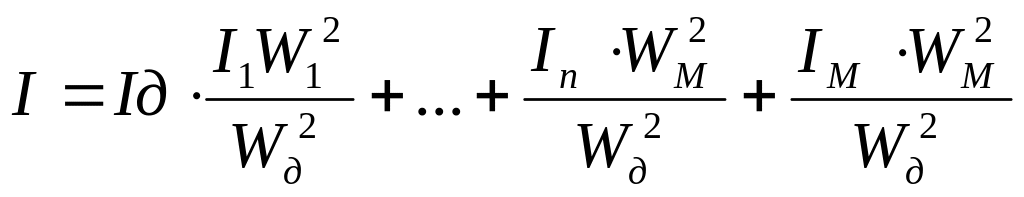
Если часть элементов системы вращается с одинаковыми скоростями, то эти элементы объедены в группы. Так для рис.1 приведен момент инерции

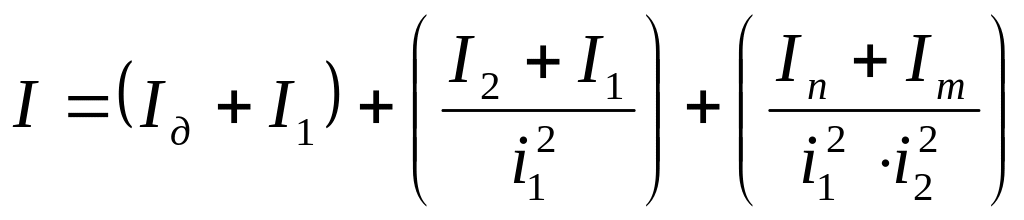
Если часть элементов системы совершает поступательные перемещения, то доп.

Если производственный механизм совершает поступательный перемещения, то

Если двигатель совершает поступательные перемещения, а производственный механизм вращается, то находится приведенная масса

m – приведенная масса

m_g – масса подвижных частей двигателя

5. Моделирование динамики разомкнутой системы

Динамика электродвигателя постоянного тока полностью описывается системой двух уравнений, первое из которых является основным уравнением двигателей постоянного тока и описывает переходные процессы в электрических цепях электродвигателя, а второе уравнение описывает механическую систему электродвигателя и построено на основании второго закона Ньютона для вращательного движения.

(1) (2)

где U- напряжение, приложенное к якорной цепи; E-э.д.с. двигателя; -активное сопротивление, ток и индуктивность якорной цепи; - активный момент двигателя и момент сопротивления, приведенный к валу двигателя; -круговая частота вращения якоря двигателя, J – момент инерции всех элементов системы, приведенный к валу электродвигателя.

Э.д.с. двигателя пропорциональна частоте вращения

, (3)

где c - конструктивный коэффициент двигателя, Ф- магнитный поток возбуждения, n- частота вращения в об/мин, c- коэффициент пропорциональности.

Активный момент двигателя пропорционален току якоря

, (4)

где - конструктивный коэффициент.

Коэффициент пропорциональности c может быть определен из формулы

где -номинальная круговая частота вращения, - частота вращения в об/мин, - номинальное напряжение , -номинальный ток якоря.

Иногда в таблицах справочных данных отсутствует одно из значений либо , тогда недостающую величину можно оценить из следующих соображений:

; ; ; .

Индуктивность якорной цепи может быть приближенно определена по формуле

где - коэффициент, равный 0,6 для двигателей без компенсационной обмотки и равный 0,25 для двигателей с компенсационной обмоткой, p- число пар полюсов двигателя.

Напишем уравнения (1) и (2) таким образом, чтобы производные тока и скорости находились в левой части

; или

; .

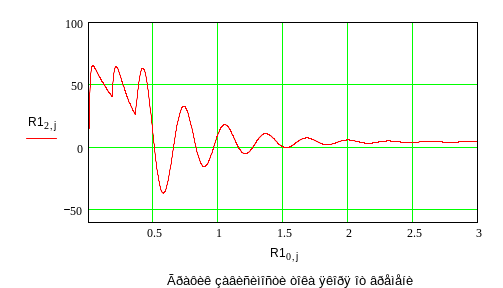
Моделирование динамики электродвигателя с приведенными нагрузками осуществляется по алгоритму, представленному на рис.2 , где n - счетчик циклов, z - количество циклов, через которое осуществляется печать, - предполагаемое время переходного процесса.

Р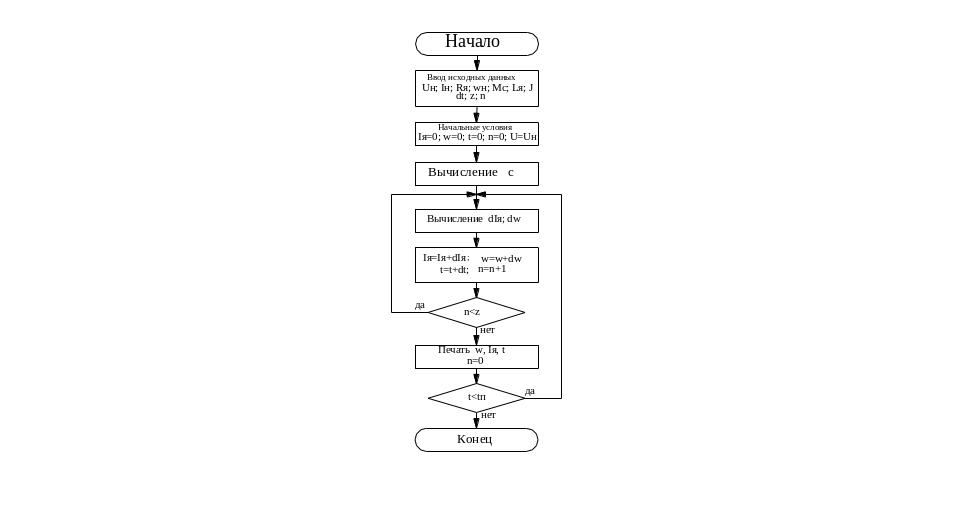 ис.2

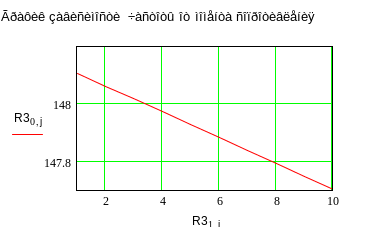
На основании моделирования необходимо построить две характеристики: механическую и регулировочную.

Механическая характеристика строится по двум точкам при некоторых значениях момента сопротивления.

Для построения регулировочной характеристики необходимо задать 6...8 значений напряжения (влево и вправо от номинального значения) и определить значения установившейся частоты вращения.

По регулировочной характеристике определяют значения минимальной и максимальной частот вращения и соответствующие им напряжения и .