
- •Основные понятия статики
- •Аксиомы статики
- •Связи и их реакции
- •Момент силы относительно точки и оси
- •Главный вектор и главный момент системы сил
- •Теорема Пуансо
- •Частные случаи приведения произвольной плоской системы сил к центру
- •Частные случаи приведения произвольной пространственной системы сил к центру
- •Уравнения равновесия различных систем сил
- •Формы уравнений равновесия плоской системы сил
- •Центр параллельных сил
- •Центр тяжести тела. Методы нахождения центра тяжести тела
- •Теорема Вариньона
- •Равновесие тела при наличии трения скольжения
- •Равновесие тела при наличии трения качения
- •Эквивалентные системы сил. Теория эквивалентности
- •Теория пар сил. Теоремы о парах
- •Статические инварианты и динамические винты
- •Центры тяжести простейших фигур
- •Фермы. Методы расчета ферм
- •Статически определенные и неопределенные задачи
- •Сила трения. Законы трения
- •Основные понятия кинематики. Скорость точки. Ускорение
- •Основные задачи кинематики точки и тела
- •Векторный, координатный и естественный способ задания движения точки
- •Определение скорости и ускорения при векторном способе задания движения.
- •Определение скорости и ускорения при координатном способе задания движения точки
- •Определение скорости и ускорения при естественном способе задания движения точки
- •Поступательное движение тела. Задание движения. Распределение скоростей и ускорений точек тела
- •Вращательное движение. Задание движения
- •Плоскопараллельное движение. Уравнение движения плоской фигуры
- •Определение скоростей при плоскопараллельном движении
Основные задачи кинематики точки и тела
Основная задача кинематики точки заключается в разработке способов задания движения точки и методов определения основных кинематических характеристик движения.
Основная задача кинематики твердого тела заключается в разработке способов задания движения и методов, позволяющих на основе небольшого числа характеристик, общих для всех точек находить кинематические характеристики каждой точки тела.
Задать движение точки, значит указать математический аппарат, с помощью которого в любой заданный наперед момент времени определить положение точки в пространстве.
Векторный, координатный и естественный способ задания движения точки
Задать движение точки, значит задать математический аппарат, с помощью которого можно в любой заданный наперед момент времени определить положение точки в пространстве.
В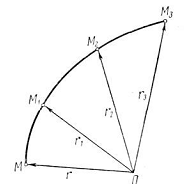 озьмем
тело отсчета. Выберем на нем некоторую
точку
О.
Чтобы определить положение точки М
в пространстве тела отсчета введем в
рассмотрение радиус-вектор.
озьмем
тело отсчета. Выберем на нем некоторую
точку
О.
Чтобы определить положение точки М
в пространстве тела отсчета введем в
рассмотрение радиус-вектор.
С
течением времени точка изменяет свое
положение в пространстве тела отсчета.
Поэтому радиус-вектор изменяется как
по направлению, так и по величине и
представляет собой некоторую векторную
функцию скалярного аргумента t,
 .
Если функция
.
Если функция
 задана или известна, то речь идет о
векторном способе задания точки.
задана или известна, то речь идет о
векторном способе задания точки.
В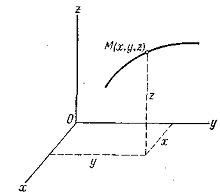 ведем
в рассмотрение тело отсчета. С телом
отсчета жестко свяжем декартовую систему
координат. Чтобы определить положение
точки М
в пространстве тела отсчета достаточно
знать ее координаты. С течением времени
координаты точки будут изменяться и
представлять собой некоторые функции
скалярного аргумента t.
ведем
в рассмотрение тело отсчета. С телом
отсчета жестко свяжем декартовую систему
координат. Чтобы определить положение
точки М
в пространстве тела отсчета достаточно
знать ее координаты. С течением времени
координаты точки будут изменяться и
представлять собой некоторые функции
скалярного аргумента t.
 .
.
Если функции известны или заданы, то речь идет о координатном способе задания движения.
П![]() усть
нам известна траектория движения точки.
На этой траектории выбираем произвольную
точку О.
Положение точки М на траектории можно
задать с помощью дуговою координаты.
усть
нам известна траектория движения точки.
На этой траектории выбираем произвольную
точку О.
Положение точки М на траектории можно
задать с помощью дуговою координаты.
С
течением времени дуговая координата
изменяется и представляет собой некоторую
функцию
 Если функция задана речь идет о
естественном способе задания движения
точки.
Если функция задана речь идет о
естественном способе задания движения
точки.
Определение скорости и ускорения при векторном способе задания движения.
При
векторном способе задания движения
положение движущейся точки в каждый
момент времени определяется радиус-вектором
 который является функцией времени
который является функцией времени
 При перемещении точки ее радиус-вектор
получает приращение
При перемещении точки ее радиус-вектор
получает приращение
 .
Отношение вектора перемещения
.
Отношение вектора перемещения
 к
промежутку времени
к
промежутку времени
 ,
в течение которого совершается это
перемещение, представляет собой вектор
средней скорости
,
в течение которого совершается это
перемещение, представляет собой вектор
средней скорости
 движения точки:
движения точки:
 .
.
В ектор
скорости точки в данный момент времени
равен производной от радиус-вектора
точки по времени:
ектор
скорости точки в данный момент времени
равен производной от радиус-вектора
точки по времени:
Вектор
скорости точки
 направлен по касательной к траектории
в сторону движения точки.
направлен по касательной к траектории
в сторону движения точки.
Допустим,
что в начальный момент точка имеет
скорость
,
а спустя время
получает приращение
 .
Разделив приращение
.
Разделив приращение
 на промежуток времени
,
получим вектор среднего ускорения этой
точки за этот промежуток времени
.
Вектор ускорения точки равен первой
производной от скорости или второй
производной от радиус-вектора точки по
времени.
на промежуток времени
,
получим вектор среднего ускорения этой
точки за этот промежуток времени
.
Вектор ускорения точки равен первой
производной от скорости или второй
производной от радиус-вектора точки по
времени.
Вектор ускорения направлен по касательной к годографу скорости — геометрическому месту концов векторов скорости движущейся точки, отложенных от одной и той же произвольной точки пространства.
