Частина друга

1. Обчислити добуток матриць та

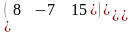1) 2) 3)

2. Знайти частинні похідні першого порядку від заданої функції

z=x·y-x²-2y²+x+10y-8

1)

2)

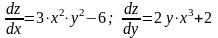
3)

3. Обчисліть визначений інтеграл:

1) 2) 3) 1.

4. Знайдіть векторний добуток [а;в] векторів

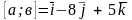1) 2) 3) .

5. Дано комплексні числа z₁ =3-7i , z₂ =3+2i. Знайти добуток цих чисел:

1) -6+21і 2) 18-9·і 3) 23-15і

6. Записати комплексне число z = в алгебраїчній формі

1. z = 2) z = 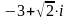3) z =

7. Знайти аргумент комплексного числа z = 1-і

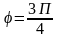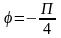1) 2) 3)

8. Записати рівняння сфери з центром у точці С(5;3;-2) і радіусом , який дорівнює 7:

1)

2)

3)

Частина третя

1. Знайти матрицю, обернену до матриці

1)

2)

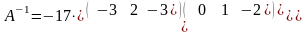
3)

2. Дано комплексні числа z₁ =-2+5i , z₂ =1-4i. Знайти частку цих чисел.

1)

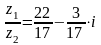
2)

3)

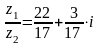
3. Знайдіть площу заштрихованої фігури:

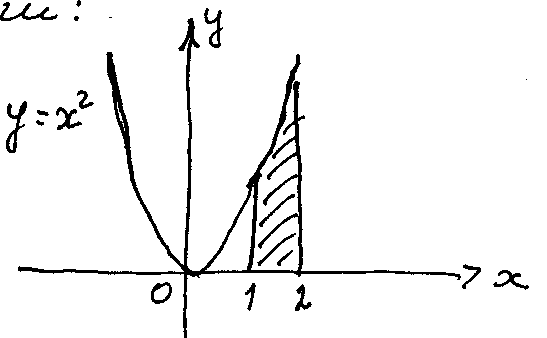
1) S=7 кв.од.

2) S= кв .од.

3) S=3 кв.од.

4. Знайдіть об’єм паралелепіпеда, побудованого на векторах

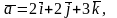
1) V=24(куб.од.)

2) V=-12(куб.од.)

3) V=12(куб.од.)

Варіант №3

Частина перша

1. Записати в радіанній мірі кут 36⁰:

1) 2) 3)

2. У якій чверті знаходиться кут α, якщо

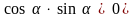
1. 2 або 3 чвертях 2) 1 або 3 чвертях 3) 1 або 4 чвертях

3. Косинус кута прямокутного трикутника рівний:

1) відношенню прилеглого катета до протилежного;

2) відношенню протилежного катета до гіпотенузи;

3) відношенню прилеглого катета до гіпотенузи.

4. Знайти arctg1:

1) 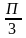2) 3)

5. Скільки критичних точок має функція у=х²-6х?

1. Жодної 2) 1 3) 2

6. Знайдіть похідну другого порядку для функції у = 4x³:

1) 2) 3)

2. Яка з функцій є первісною для функції у = 4x³?

1. F(x) =12 x²+1 2) F(x) = 12x 3) F(x) = x⁴

8. Чому дорівнює похідна ?

1) 2) 3)

9. Чому дорівнює інтеграл ?

1) 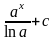2) 3) .

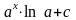10. Для диференціального рівняння , скласти характеристичне рівняння:

1) к² -4к+4=0; 2) к² +4к+4=0; 3) к³ +4к² +4к=0.

11. Множина всіх первісних для функції на деякому проміжку називається:

1) визначеним інтегралом; 2) невизначеним інтегралом; 3) первісною.

12. Знайдіть загальний вигляд первісної функції .

1) 2) 3)

13. Точки, в яких друга похідна змінює свій знак, називаються:

1. критичними;

2. екстремальними точками;

3. точками перегину .

14. Обчислити визначник другого порядку: :

1) -14 2) 10 3) 14

15. Алгебраїчне доповнення елемента а₂₂ для визначника дорівнює:

1) -5 2) -11 3) 5

16. Обчислити визначник 3-го порядку :

1) 210 2) 109 3) -124

17. Добуток матриці В^Т =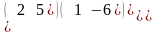 на число 2 дорівнює:

1. 2·В^Т= 2) 2·В^Т= 3) 2·В^Т= .

18. Визначити тип матриці:

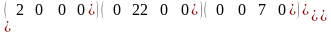
1) одинична 2) трикутна 3) діагональна

19. Для даних матриць вказати еквівалентні:

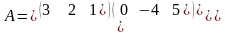
1. матриці: А і С 2) матриці: А і В 3) матриці: В і С

20. Дано комплексне число виду z=5+9i. Визначити дійсну частину.

1. 5 2) 9 3) 9і.

21. Вибрати з вказаних пар комплексних чисел, протилежні:

1. z = 6+8i та z =6-8i

2. z= -6+8i та z =-6 - 8i

3. z=6-8i та z=-6 + 8i

22. В якій чверті знаходиться комплексне число z=2 + 3i:

1. в ІІ чверті.

2. в І чверті.

3. в ІVчверті.

23. Дано комплексні числа z₁ =3-2i і z₂ =6-17i. Знайти різницю z ₁- z ₂:

1. z ₁- z ₂= 9+15і

2. z ₁- z ₂=-3+15і

3. z ₁- z ₂= 9-15і

24. Дано модуль комплексного числа z = 2 і аргумент . Записати тригонометричну форму комплексного числа:

1) z =

2) z =

3) z =

25. Вектори називаються компланарними, якщо:

1) кожен з них перпендикулярний одній площині

2) кожен з них паралельний одній площині

3) кожен з них паралельний одній прямій

26. Скалярний добуток двох векторів на площині знаходиться за формулою:

1. ;

2. ;

3. .