4) Импликация. Импликацией двух высказываний p и q называется высказывание, истинное тогда и только тогда, когда высказывание р истинно, а q – ложно.
Обозначается PQ (или РQ). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.
-
P
Q
PQ
И
И
И
И
Л
Л
Л
И
И
Л
Л
И
5) Эквиваленция. Эквиваленцией двух высказываний p и q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают.
Обозначается РQ или РQ.
-
P
Q
PQ
И
И
И
И
Л
Л
Л
И
Л
Л
Л
И
С помощью этих основных таблиц истинности можно составлять таблицы истинности сложных формул.
Пример. С помощью таблиц истинности проверить, являются ли эквивалентными формулы и .
Составим таблицы истинности для каждой формулы:
-
p
r
(pr)
И
И
Л
И
И
И
Л
Л
Л
И
Л
И
И
Л
Л
Л
Л
И
Л
Л
-
p
r
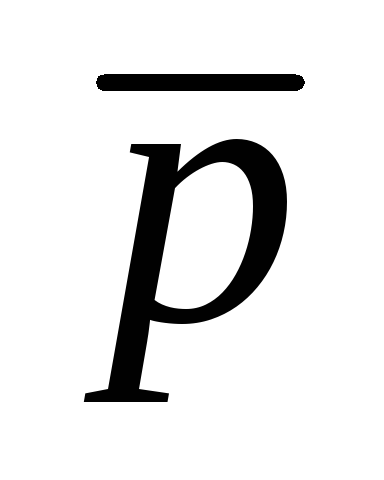
И
И
Л
Л
Л
И
И
Л
Л
И
И
И
Л
И
И
Л
И
И
Л
Л
И
И
И
И
Данные формулы не являются эквивалентными.
Пример. С помощью таблиц истинности проверить, являются ли эквивалентными формулы и .
Составим таблицы истинности для заданных формул.
-
p
q
r
pq
(pq)r
И
И
И
И
И
И
И
Л
И
И
И
Л
И
Л
И
И
Л
Л
Л
Л
Л
И
И
Л
И
Л
И
Л
Л
Л
Л
Л
И
И
И
Л
Л
Л
И
И
|
p |
q |
r |
pq |
qp |
(pq)(qp) |
(pq)(qp)r |
|
И |
И |
И |
И |
И |
И |
И |
|
И |
И |
Л |
И |
И |
И |
И |
|
И |
Л |
И |
Л |
И |
И |
И |
|
И |
Л |
Л |
Л |
И |
И |
И |
|
Л |
И |
И |
И |
Л |
И |
И |
|
Л |
И |
Л |
И |
Л |
И |
И |
|
Л |
Л |
И |
И |
И |
И |
И |
|
Л |
Л |
Л |
И |
И |
И |
И |
Из составленных таблиц видно, что данные формулы не равносильны.
Основные равносильности.
Для любых формул А, В и С справедливы следующие равносильности:
A & B B & A; A & A A; A & (B & C) (A & B) & C;
A B B A; A A A; A (B C) (A B) C;
A (B & C) (A B) & (A C); A & (B C) (A & B) (A & C);
A & (A B) A; A (A & B) A; A A; (A & B) A B;
A (A & B) (A & B); A (A B) & (A B);
Булевы функции.
Определение. Булевой функцией f(X1, X2, …, Xn) называется называется произвольная n – местная функция, аргументы и значения которой принадлежат множеству {0, 1}.
Вообще говоря между логическими высказываниями, логическими связками и булевыми функциями просматривается явная аналогия. Если логические функции могут принимать значения истинно или ложно, то для булевой функции аналогами этих значений будут значения 0 или 1.
Для булевых функций также можно составить таблицы значений, соответствующим основным логическим операциям.
|
X1 |
X2 |
X1 |
X1&X2 |
X1X2 |
X1X2 |
X1X2 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |