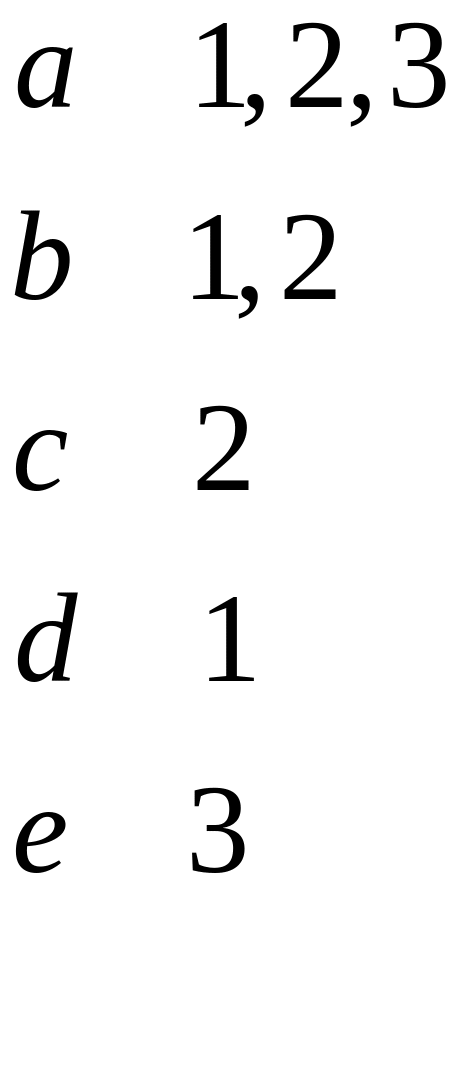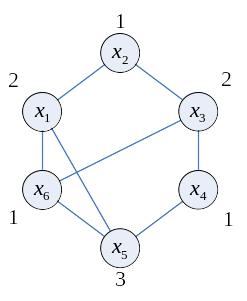
Алгоритм нахождения раскраски (хроматического числа)

1) Выделить все пустые подграфы графа. 2) Построить таблицу покрытий вершин графа пустыми подграфами. 3) Найти минимальное покрытие вершин графа пустыми подграфами (мощность минимального покрытия – это , а само покрытие определяет раскраску).

Пример

1 1 1 1 1 1 1 1 1 1 1

Оценки хроматического числа

1. Теорема Кенига Граф бихроматичен ( ) тогда и только тогда, когда в нет циклов нечетной длины.

2. Теорема , где - плотность графа .

3. Теорема , где - степень графа .

4. Оценка Бержа , где - число внешней устойчивости графа .

5.

Теорема , где , . , где , . , где , . , где .

Примеры

а) Графы не имеют общих вершин. По теореме выше . б) Графы имеют по одной общей вершине. Отметим для нечетного цикла следующую раскраску: одна вершина в 3-й цвет, остальные в 1-й и 2-й цвета поочередно. На нашем графе вначале раскрасим в два цвета четный цикл (вместе с общей вершиной). Теперь рассмотрим нечетный цикл. В нем общая вершина оказалась закрашена каким-то цветом. Считаем этот цвет 3-им и закрашиваем все остальные вершины поочередно в два цвета (отличные от ранее выбранных, так как имеем граф суммы). Итого использовали четыре цвета. . в) Графы имеют по две общие, не смежные между собой вершины. Так как между двумя смежными вершинами в обоих графах будет располагаться цепь длиной, по крайней мере, , соединенная с аналогичной цепью в другой части графа всеми возможными связями, то . Для четырех цветов раскраска существует всегда: сначала раскрашиваем четный цикл в два цвета, затем оставшиеся цепи нечетного цикла закрашиваем в другие два цвета. .

Алгоритм приближенной раскраски графа (алгоритм Ершова)

Алгоритм основан на стягивании несмежных вершин:

Стягивание проводить до тех пор, пока не получим полный граф. Мощность этого полного графа является оценкой хроматического числа сверху, а сам полный граф определяет приближенную раскраску графа.

Замечание В первую очередь желательно стягивать те вершины, расстояние между которыми четно.

Пример

Задача Есть 3 предприятия, на которых должны выпускаться 11 изделий. Каждый тип изделий должен выпускаться только на одном предприятии. При выпуске изделий разного типа ( ) могут использоваться общие детали и материалы. Для каждой пары изделий указан процент общих деталей и материалов. Необходимо распределить изделия по предприятиям так, чтобы на одном предприятии выпускались детали с наибольшим процентом общих деталей. Критерий: Минимум общих поставок для изделий, выпускаемых на одном предприятии был как можно больше.

	55
	60	80
	85	65	40
	45	90	35	80
	80	75	30	90	90
	50	30	70	35	65	30
	50	60	90	40	35	70	30
	60	45	40	80	30	70	20	25
	45	40	45	35	80	20	90	25	85
	80	70	85	30	35	40	25	75	75	60

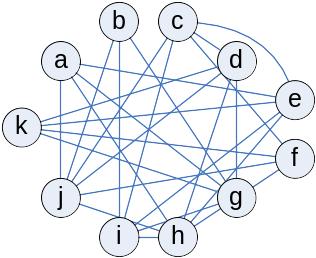
Граф несовместимости изделий

	Раскраска:
	Раскраска:
	Раскраска:
	Раскраска:

Решение - I предп. II предп. III предп.