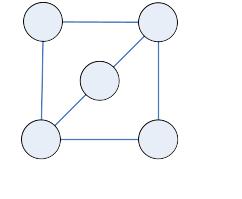
- •Основные объекты графов
- •Способы задания графов
- •Графический способ задания графов.
- •Изоморфизм на графах
- •Элементы графов
- •Степень вершины. Степень графа
- •Типы графов
- •Операции на графах
- •Связность в графах Понятие цепи
- •Связность графа
- •Компоненты связности графа
- •Нахождение компонент связности
- •Связность в орграфах
- •Цикломатика графа
- •Алгоритм нахождения базисной системы циклов
- •Разделяющие множества. Разрезы
- •Алгоритм нахождения базисной системы разрезов
- •Устойчивость графа Внешняя устойчивость графа
- •Внешняя устойчивость орграфа
- •Внутренняя устойчивость графа
- •Алгоритм нахождения пустых подграфов
- •Полные подграфы. Плотность графа
- •Алгоритм нахождения полных подграфов
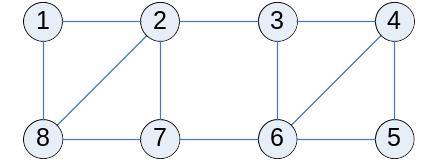
Компоненты связности графа
Максимальный по
включению вершин подграф графа, любые
две вершины которого связны (имеется
ввиду вершины подграфа) называется
компонентой связности графа.
![]() - число компонент связности графа.
- число компонент связности графа.
Теорема Любая вершина графа принадлежит ровно одной компоненте связности.
Число компонент
связности графа
является инвариантом. Если
![]() ,
то граф связен. Инварианты
,
то граф связен. Инварианты
![]() и
и
![]() являются зависимыми друг от друга.
являются зависимыми друг от друга.
Теорема

Следствие
Если
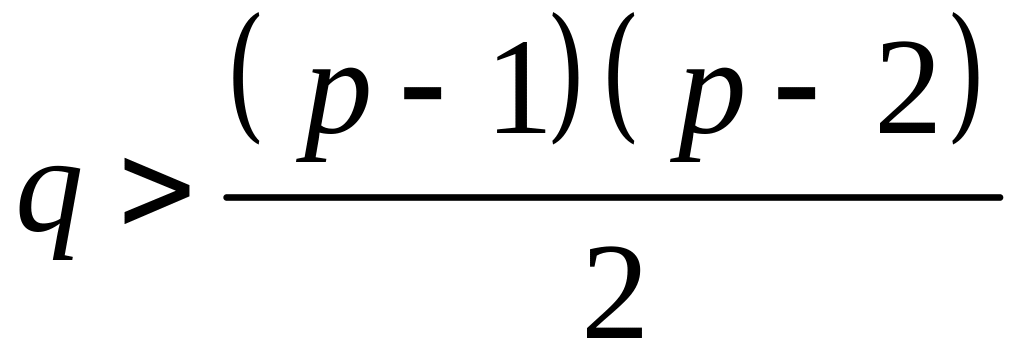 ,
то граф связен (
,
то граф связен (![]() ).
).
Нахождение компонент связности

![]()
Шаг 0: поместить
в список.
Итерационный шаг:
1.
Найти в списке первую непросмотренную
вершину (
).
2.
Вычислить
![]() и добавить в список те вершины из
окрестности, которых нет в списке.
3.
Отметить
как просмотренную.
Заключительный
шаг: Итерационный шаг выполняется до
тех пор пока в списке есть непросмотренные
вершины.
и добавить в список те вершины из
окрестности, которых нет в списке.
3.
Отметить
как просмотренную.
Заключительный
шаг: Итерационный шаг выполняется до
тех пор пока в списке есть непросмотренные
вершины.
Связность в орграфах
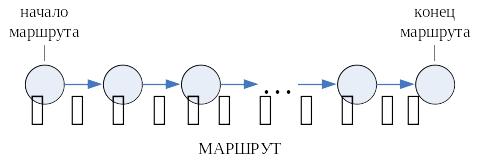
Если начальная
вершина совпадает с конечной, то такой
маршрут называется контуром. Две
вершины
и
сильно связны, если существует
маршрут
![]() и существует маршрут
и существует маршрут
![]() .
.
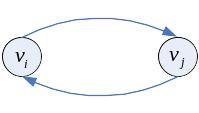
Орграф называется сильно связным, если любые две его вершины сильно связны.
Пример
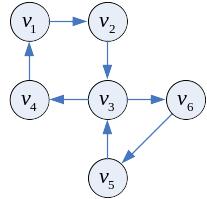
Максимальный по включению вершин подграф орграфа, любые две вершины которого сильно связны, называется компонентой сильной связности орграфа (КСС).
Отношение сильной связности является отношением эквивалентности на множестве вершин. Таким образом разбиение орграфа на КСС – это разбиение множества вершин на классы эквивалентности.
Нахождение КСС
Теорема
Любая
вершина орграфа принадлежит ровно одной
КСС орграфа.
![]()
![]() ,
где
,
где
![]() - множество вершин, достижимых из
,
- множество вершин, достижимых из
,
![]() - множество вершин, из которых достижимо
.
- множество вершин, из которых достижимо
.


![]()
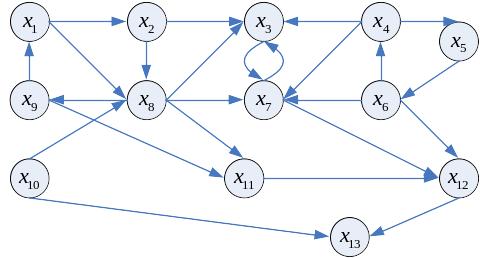
Пример
![]() - группировка,
- группировка,
![]() - отношение влияния.
- отношение влияния.
Кланы – совокупности группировок с равными «правами» по отношению друг к другу и к внешним группировкам.
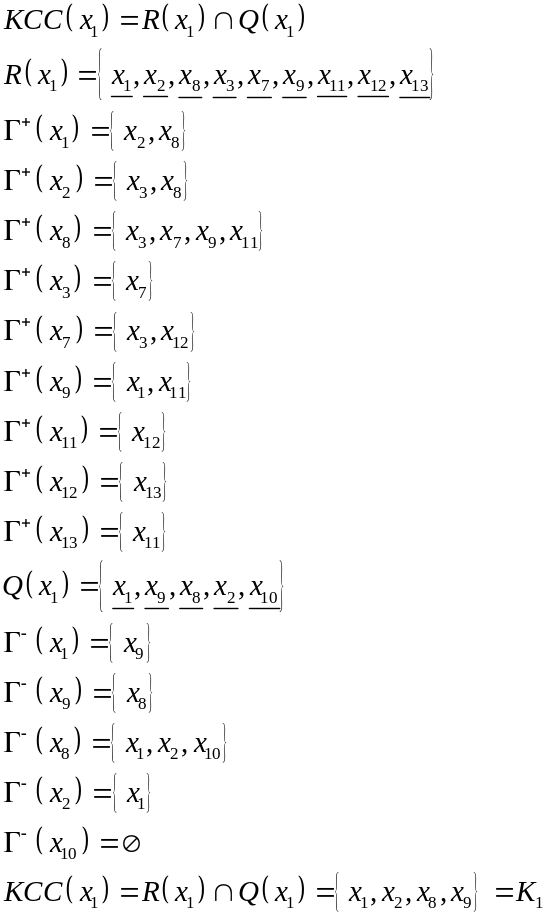




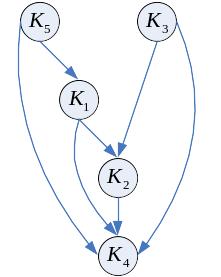
![]()

Сети
Орграф, в котором отсутствуют контуры, называется сетью. В сети есть следующие особые элементы:
вершина-исток
( |
вершина-сток
( |
Каждая вершина в
сети является компонентой сильной
связности. Пусть
![]() - орграф и
- орграф и
![]() - его КСС. Конденсатом орграфа
называется сеть, которая получена из
орграфа путем сжатия каждой КСС в одну
вершину.
- его КСС. Конденсатом орграфа
называется сеть, которая получена из
орграфа путем сжатия каждой КСС в одну
вершину.
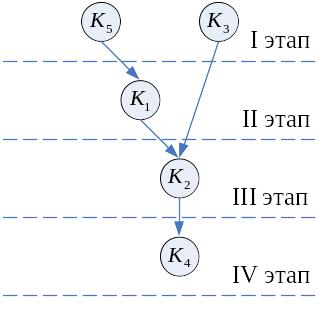
Циклы в графе
Эйлеровы и Гамильтоновы циклы
Цикл в графе называется Эйлеровым, если любое ребро графа участвует в его образовании ровно один раз. Граф, содержащий Эйлеров цикл называется Эйлеровым.
Теорема Эйлера Граф является Эйлеровым тогда и только тогда, когда степени всех его вершин четные.
Цикл в графе называется Гамильтоновым, если каждая вершина графа участвует в его образовании ровно один раз. Граф, содержащий Гамильтонов цикл называется Гамильтоновым.
Свойства «Эйлеровости» и «Гамильтоновости» являются независимыми.
|
|
|
|
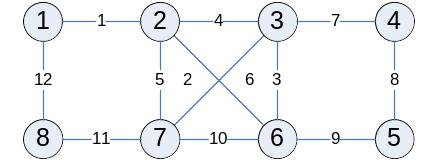
Цикломатика графа
Пусть
- граф. Цикл в графе может быть записан
в виде
![]() ,
где
,
где

Пример
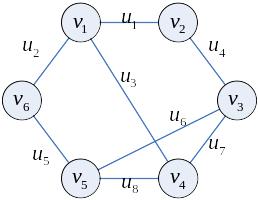
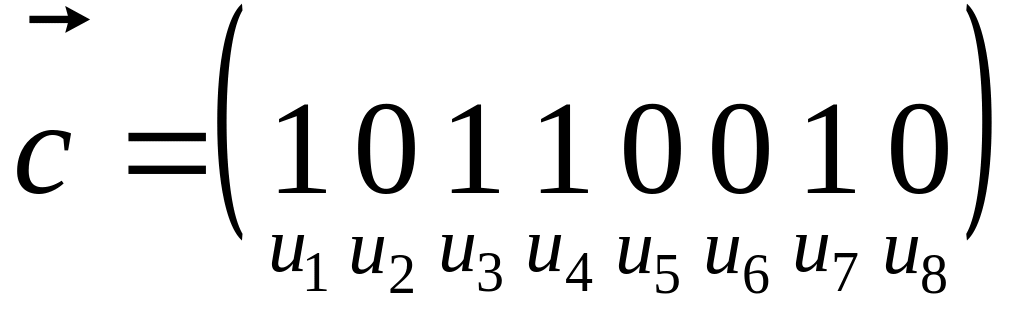
Каждый цикл может
быть представлен в качестве двоичного
вектора. Множество циклов образует
пространство двоичных векторов.
Цикломатический базис – совокупность
линейно независимых циклов графа, с
помощью которых могут быть получены
все остальные циклы. Цикломатическое
число графа
![]() - мощность базисной системы циклов графа
.
- мощность базисной системы циклов графа
.
![]()
Пример
![]()
Граф, у которого цикломатическое число равно 0, называется деревом (или ациклическим графом). Многокомпонентный ациклический граф называется деревом. Остов графа – частичный граф исходного графа, в котором число вершин и число компонент связности совпадает с числом вершин и числом компонент связности исходного графа, но цикломатическое число равно 0.