
- •Глава 2.Численные методы математического анализа Часть 1.Интерполирование и приближение функций
- •§1. Интерполирование алгебраическими многочленами п. 1.1. Определение интерполяционного многочлена
- •П. 1.2. Интерполяционная формула Лагранжа
- •П. 1.3. Интерполяционная формула Ньютона
- •П. 1.4. Погрешность интерполяционной формулы
- •§2. Сплайн-интерполирование п. 2.1. Построение кубического сплайна
- •П. 2.2.Метод прогонки
- •§3. Приближение функций эмпирическими формулами
- •П. 3.1. Подбор эмпирической формулы
- •П. 3.2. Подбор параметров для выбранного типа эмпирической формулы
- •П. 3.2.1. Метод средних
- •П. 3.2.2. Среднеквадратичное приближение
- •Часть 2.Численное интегрирование §1.Простейшие квадратурные формулы п. 1.1.Постановка задачи
- •П. 1.2.Формула прямоугольников
- •П. 1.3.Формула трапеций
- •П. 1.4.Формула Симпсона (парабол)
- •§2.Квадратурные формулы интерполяционного типа п. 2.1.Вывод формул
- •П. 2.2.Оценка погрешности
- •§3.Квадратурные формулы наивысшей алгебраической степени точности
П. 1.3.Формула трапеций
Введем на равномерную сетку с шагом h
.
На частичном отрезке формула трапеций имеет вид
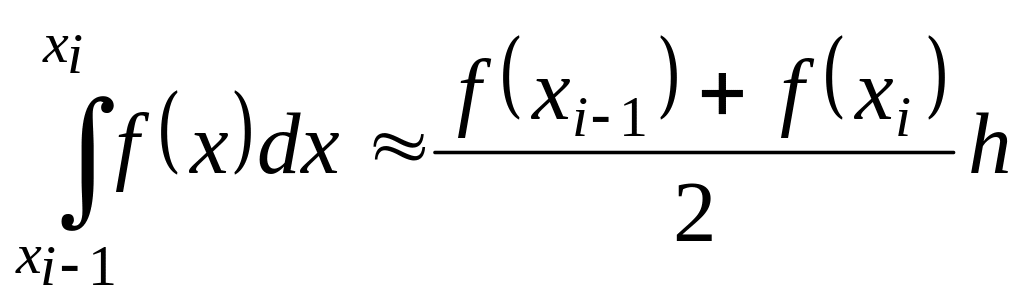 (1.10)
(1.10)
Она
получается путем замены подынтегральной
функции
интерполяционным многочленом первой
степени, построенным по узлам
![]() ,
т.е. функцией
,
т.е. функцией
![]() (*)
(*)
Погрешность
интерполяционной формулы имеет вид
![]() ,
следовательно, для многочлена (*) получаем
,
следовательно, для многочлена (*) получаем
![]()
Тогда,
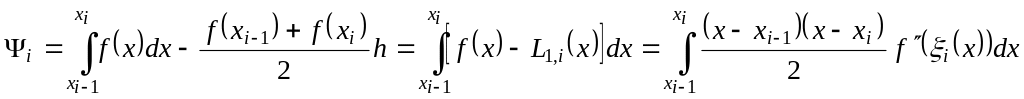
Следовательно,
![]() , (1.11)
, (1.11)
где .
Оценка
(1.12) неулучшаема, так как в ней достигается
равенство, например, для
![]() .
.
Составная формула трапеций имеет вид
![]() , (1.12)
, (1.12)
где
![]()
Погрешность этой формулы оценивается следующим образом
![]() , (1.13)
, (1.13)
где .
Таким
образом, формула трапеций имеет второй
порядок точности
![]() ,
но ее погрешность оценивается в два
раза большей величиной, чем погрешность
метода прямоугольников.
,
но ее погрешность оценивается в два
раза большей величиной, чем погрешность
метода прямоугольников.
П. 1.4.Формула Симпсона (парабол)
Введем на отрезке равномерную сетку с шагом h
.
При
аппроксимации интеграла (1.4) заменим
функцию
параболой, проходящей через точки
![]() ,
т.е. представим
в виде
,
т.е. представим
в виде
![]() ,
,
где
![]() - интерполяционный многочлен Лагранжа
второй степени:
- интерполяционный многочлен Лагранжа
второй степени:
![]()
Проводя интегрирование, получим
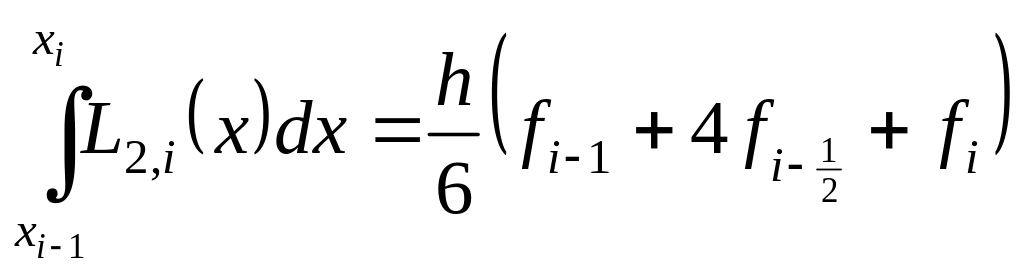 ,
,
где
![]() ,
,
![]() .
.
Таким образом, приходим к приближенному равенству
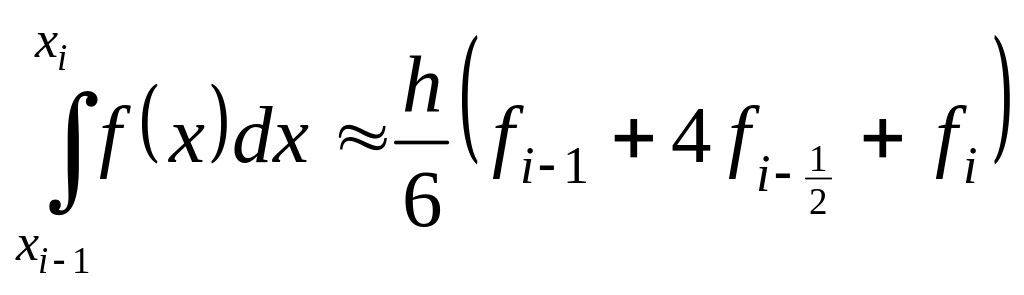 (1.14)
(1.14)
Эта формула называется формулой Симпсона или формулой парабол.
На всем отрезке
![]() формула Симпсона имеет вид
формула Симпсона имеет вид
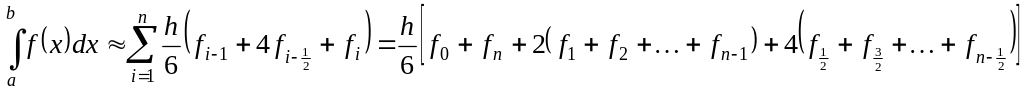 (
1.0)
(
1.0)
Чтобы не использовать дробных индексов, можно обозначить
![]() .
.
Тогда формулу Симпсона можно записать следующим образом
![]() (1.15)
(1.15)
Погрешность
![]() формулы (1.15) оценивается следующим
образом
формулы (1.15) оценивается следующим
образом
![]() , (1.16)
, (1.16)
где
![]() .
.
Погрешность составной формулы Симпсона (1.17) оценивается так:
![]() , (1.17)
, (1.17)
где
![]() ,
,
![]() .
.
Отсюда
видно, что формула Симпсона существенно
точнее, чем формулы прямоугольников и
трапеций. На частичном отрезке она
имеет пятый порядок точности (![]() ),
а на всем отрезке – четвертый порядок
точности (
),
а на всем отрезке – четвертый порядок
точности (![]() ).
).
§2.Квадратурные формулы интерполяционного типа п. 2.1.Вывод формул
Будем рассматривать формулы приближенного вычисления интегралов
![]() , (2.1)
, (2.1)
где
![]() - заданная интерполируемая функция
(так называемая весовая функция),
- заданная интерполируемая функция
(так называемая весовая функция),
![]() -
достаточно гладкая функция.
-
достаточно гладкая функция.
Рассматриваемые далее формулы имеют вид
![]() ,
(2.2)
,
(2.2)
где
![]() ,
,
![]() - числовые коэффициенты,
- числовые коэффициенты,
![]() .
.
Квадратурные
формулы будем получать путем замены
интерполяционным многочленом сразу
на всем отрезке
.
Полученные таким образом формулы
называются квадратурными формулами
интерполяционного типа. Как правило,
точность этих формул возрастает с
увеличением числа узлов интерполирования.
Формулы прямоугольников, трапеций и
Симпсона являются частным случаем
квадратурных формул интерполяционного
типа, когда
![]() ,
,
![]() .
.
Получим выражения для коэффициентов квадратурных формул интерполяционного типа.
Пусть
на
заданы узлы интерполирования
![]() .
Предполагается, что среди этих узлов
нет совпадающих, в остальном они могут
быть расположены как угодно на
.
Заменим в интеграле (2.1) функцию
интерполяционным многочленом Лагранжа
.
Предполагается, что среди этих узлов
нет совпадающих, в остальном они могут
быть расположены как угодно на
.
Заменим в интеграле (2.1) функцию
интерполяционным многочленом Лагранжа
,
где
![]() ,
,
![]() .
.
Получим приближенную формулу вида (2.2), где
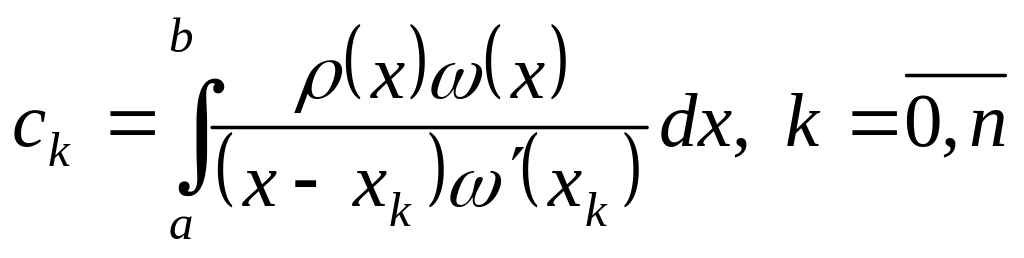 (2.3)
(2.3)
Таким образом, формула (2.2) является квадратурной формулой интерполяционного типа тогда и только тогда, когда ее коэффициенты вычисляются по правилу (2.3).
