
- •Глава 2.Численные методы математического анализа Часть 1.Интерполирование и приближение функций
- •§1. Интерполирование алгебраическими многочленами п. 1.1. Определение интерполяционного многочлена
- •П. 1.2. Интерполяционная формула Лагранжа
- •П. 1.3. Интерполяционная формула Ньютона
- •П. 1.4. Погрешность интерполяционной формулы
- •§2. Сплайн-интерполирование п. 2.1. Построение кубического сплайна
- •П. 2.2.Метод прогонки
- •§3. Приближение функций эмпирическими формулами
- •П. 3.1. Подбор эмпирической формулы
- •П. 3.2. Подбор параметров для выбранного типа эмпирической формулы
- •П. 3.2.1. Метод средних
- •П. 3.2.2. Среднеквадратичное приближение
- •Часть 2.Численное интегрирование §1.Простейшие квадратурные формулы п. 1.1.Постановка задачи
- •П. 1.2.Формула прямоугольников
- •П. 1.3.Формула трапеций
- •П. 1.4.Формула Симпсона (парабол)
- •§2.Квадратурные формулы интерполяционного типа п. 2.1.Вывод формул
- •П. 2.2.Оценка погрешности
- •§3.Квадратурные формулы наивысшей алгебраической степени точности
П. 3.2. Подбор параметров для выбранного типа эмпирической формулы
Пусть выбрана эмпирическая формула типа
![]() , (3.1)
, (3.1)
где
![]() - неизвестные параметры.
- неизвестные параметры.
Определение
3.1.
Величина
![]() (3.2)
(3.2)
называется отклонением от экспериментальных данных.
П. 3.2.1. Метод средних
Для
определения параметров в формуле , (3.1)
можно применить метод средних, а именно
условие равенства нулю суммы отклонений
![]() во всех точках
во всех точках
![]() (3.3)
(3.3)
Имеем
одно уравнение с
![]() неизвестным. Для однозначной разрешимости
разбиваем (3.3) на систему из
уравнений, например
неизвестным. Для однозначной разрешимости
разбиваем (3.3) на систему из
уравнений, например
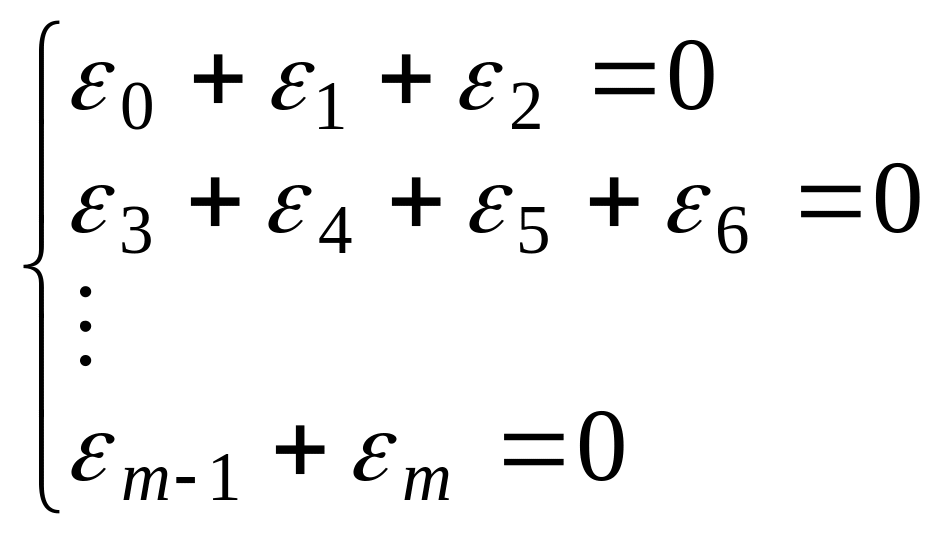 (3.4)
(3.4)
Так
как систему (3.4) можно составит по-разному,
то и получаемые решения (значения
параметров
![]() )
будут различными.
)
будут различными.
П. 3.2.2. Среднеквадратичное приближение
Рассмотрим как величину аппроксимации величину
![]() (3.5)
(3.5)
Параметры
функции (3.1) будем искать таким образом,
чтобы они минимизировали функцию
![]() ,
определенную по формуле (3.5).
,
определенную по формуле (3.5).
Решение задачи о нахождении параметров в такой постановке называется методом наименьших квадратов.
Необходимые
условия минимума функции
![]() дают систему уравнений:
дают систему уравнений:
![]() (3.6)
(3.6)
Если
![]() (3.7)
(3.7)
где
![]() - линейно независимые функции, тогда
система уравнений (3.6) будет линейной.
- линейно независимые функции, тогда
система уравнений (3.6) будет линейной.
На практике часто используются функции
![]() .
(3.8)
.
(3.8)
Тогда
![]() (3.9)
(3.9)
многочлен
степени
![]() .
Следовательно,
.
Следовательно,
![]()
![]()
![]()
![]()
Таким образом, из (3.6) получаем систему следующего вида:
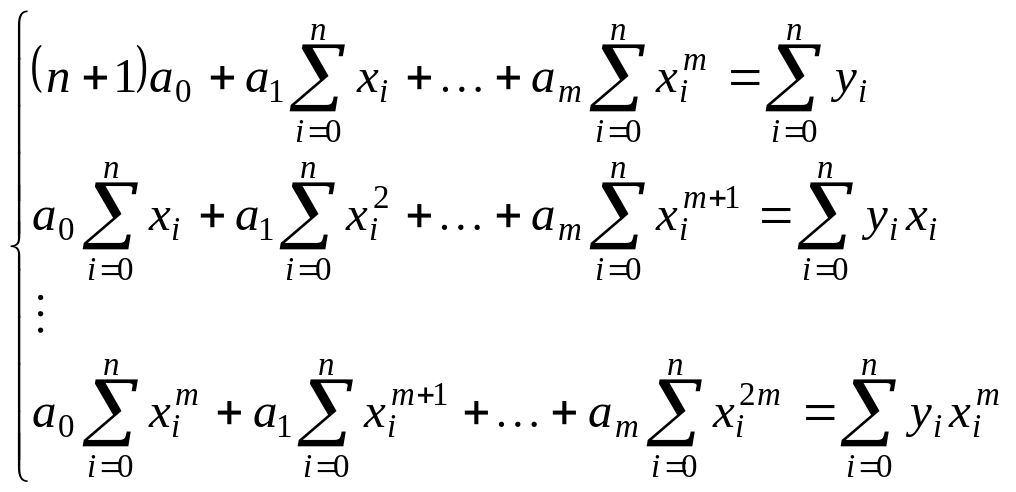 (3.10)
(3.10)
При
![]() полученный многочлен совпадает с
интерполяционным многочленом Лагранжа.
полученный многочлен совпадает с
интерполяционным многочленом Лагранжа.
Часть 2.Численное интегрирование §1.Простейшие квадратурные формулы п. 1.1.Постановка задачи
Задача численного интегрирования состоит в нахождении приближенного значения интеграла
![]() ,
(1.1)
,
(1.1)
где - заданная функция.
На
отрезке
вводится сетка
![]() .
В качестве приближенного значения
интеграла рассматривается число
.
В качестве приближенного значения
интеграла рассматривается число
![]() ,
(1.2)
,
(1.2)
где - числовые коэффициенты.
Определение
1.1.
Приближенное равенство
![]() называется квадратурной
формулой.
Сумма
называется квадратурной
формулой.
Сумма
![]() называется квадратурной
суммой.
Точки
называется квадратурной
суммой.
Точки
![]() - узлами
квадратурной формулы,
числа
- коэффициентами
квадратурной формулы.
Разность
- узлами
квадратурной формулы,
числа
- коэффициентами
квадратурной формулы.
Разность
![]() называется погрешностью
квадратурной формулы.
называется погрешностью
квадратурной формулы.
Задача
численного интегрирования при помощи
квадратур состоит в отыскании таких
узлов
![]() и таких коэффициентов
и таких коэффициентов
![]() ,
чтобы погрешность квадратурной формулы
была минимальной для функций из заданного
класса.
предполагается достаточной гладкой.
,
чтобы погрешность квадратурной формулы
была минимальной для функций из заданного
класса.
предполагается достаточной гладкой.
При построении квадратурной формулы интеграл (1.1) обычно представляют в виде суммы интегралов по частичным отрезкам:
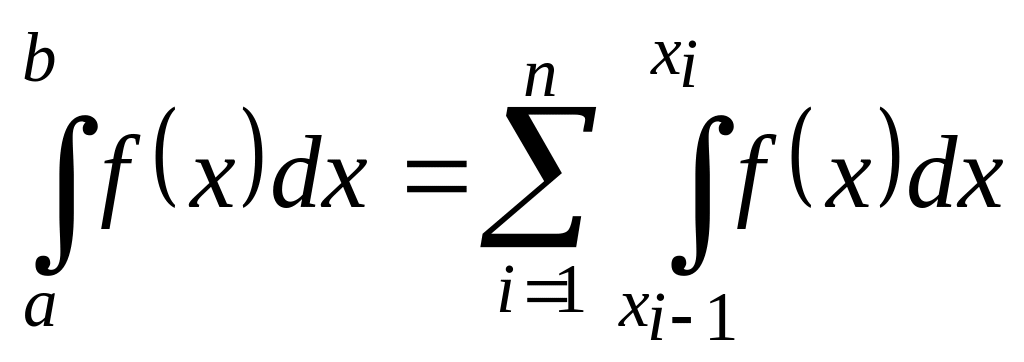 (1.3)
(1.3)
Для построения формулы численного интегрирования на всем отрезке достаточно построить квадратурную формулу для интеграла
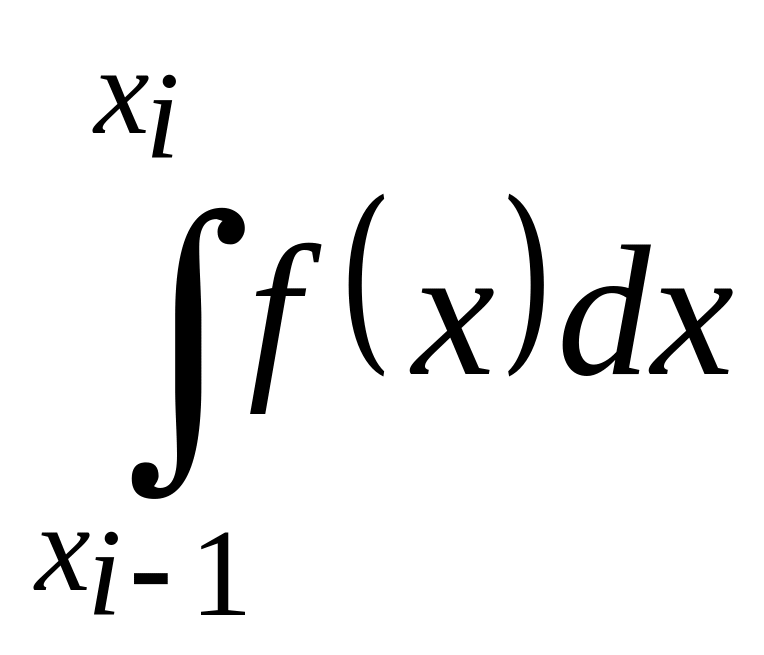 (1.4)
(1.4)
на частичном
отрезке
![]() и воспользоваться свойством (1.3).
и воспользоваться свойством (1.3).
П. 1.2.Формула прямоугольников
Введем на отрезке равномерную сетку с шагом h
![]() .
.
Заменим
интеграл (1.4) выражением
![]() ,
где
,
где
![]() .
.
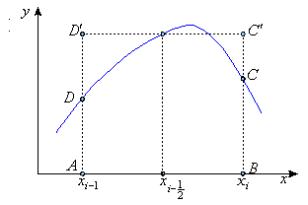
Геометрически
такая замена означает, что площадь
криволинейной трапеции ABCD
заменяется площадью прямоугольника
![]() .
.
Тогда получим формулу
 (1.0)
(1.0)
Она называется формулой средних прямоугольников на частичном отрезке .
Погрешность
метода определяется величиной
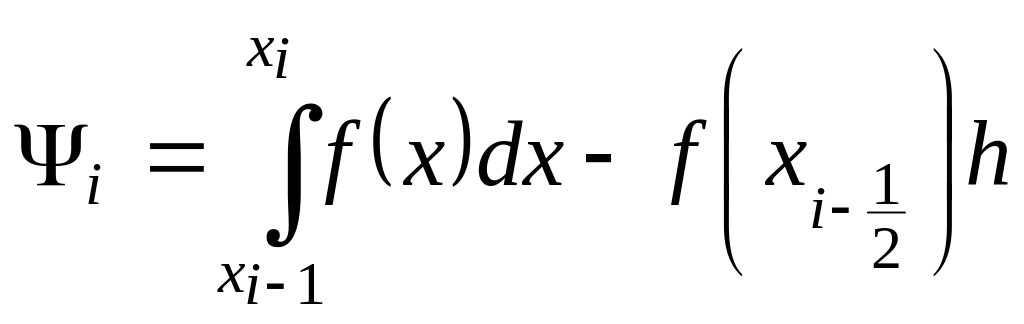 .
Ее легко можно оценить с помощью формулы
Тейлора. Действительно, запишем
.
Ее легко можно оценить с помощью формулы
Тейлора. Действительно, запишем
![]() в следующем виде
в следующем виде
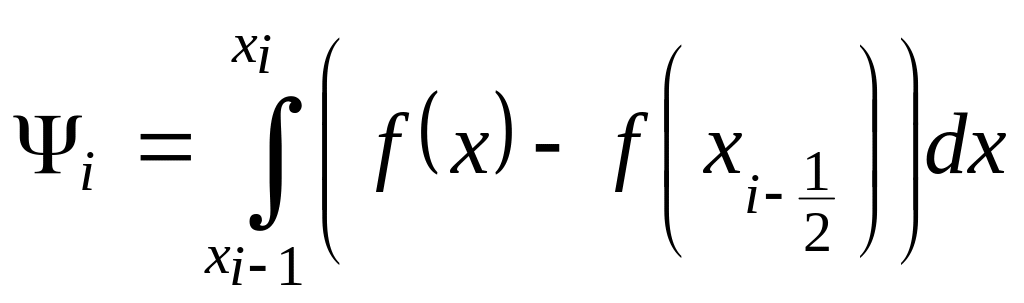 ,
(1.5)
,
(1.5)
воспользуемся разложением
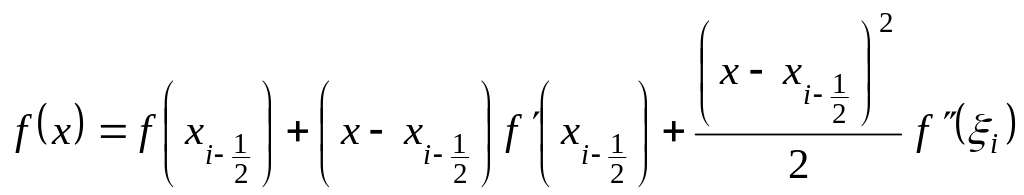 ,
,
где
![]() .
.
Тогда из (1.6) получим
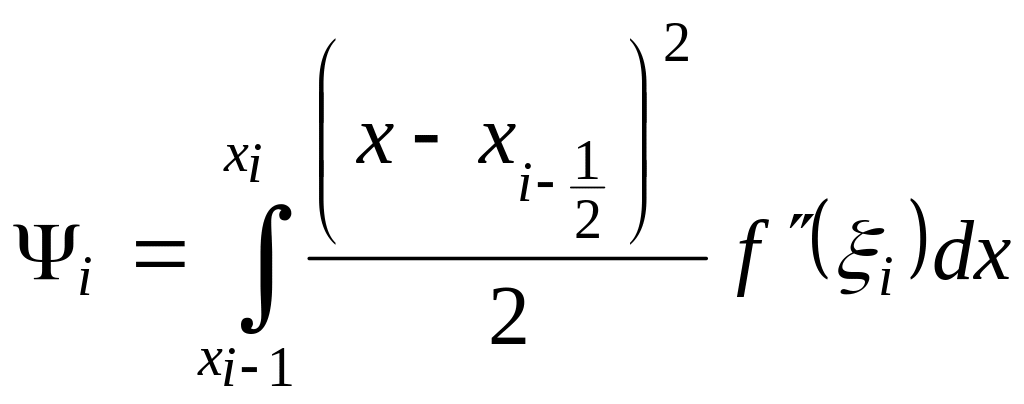
Обозначим
![]() ,
тогда погрешность
можно оценить следующим образом
,
тогда погрешность
можно оценить следующим образом
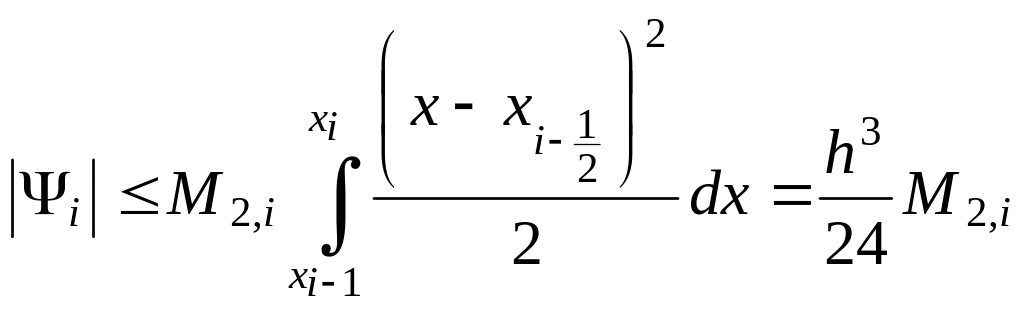
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка
![]() ,
(1.6)
,
(1.6)
т.е.,
формула имеет погрешность
![]() при
при
![]() .
Оценка (1.7) неулучшаема, т.е. существует
формула для которой оценка (1.7) выполняется
со знаком равенства (например,
.
Оценка (1.7) неулучшаема, т.е. существует
формула для которой оценка (1.7) выполняется
со знаком равенства (например,
![]() ).
).
Суммируя
равенство (1.5) по
![]() ,
получим составную формулу прямоугольников
,
получим составную формулу прямоугольников
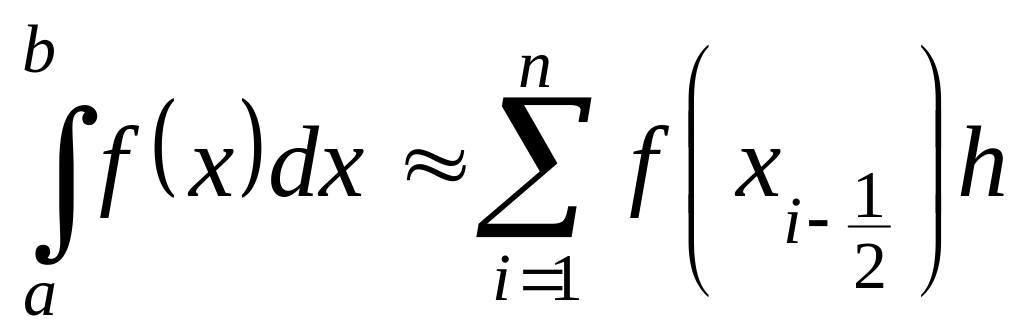 (1.7)
(1.7)
Погрешность
этой формулы
 равна сумме погрешностей по всем
частичным отрезкам
равна сумме погрешностей по всем
частичным отрезкам
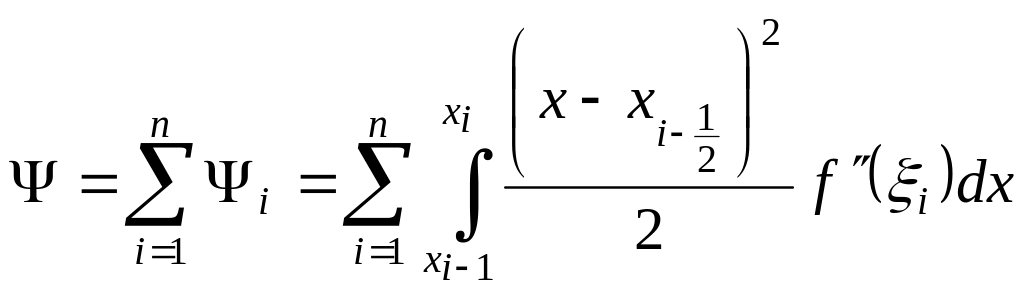 (1.8)
(1.8)
Обозначим
![]() ,
тогда из (1.9) получаем
,
тогда из (1.9) получаем
![]() , (1.9)
, (1.9)
т.е.,
погрешность формулы прямоугольников
на всем отрезке есть величина
![]() при
.
В этом случае говорят, что квадратурная
формула имеет второй
порядок точности.
при
.
В этом случае говорят, что квадратурная
формула имеет второй
порядок точности.
