П. 2.2.Метод прогонки

Рассмотрим систему линейных уравнений

(2.13)

(2.14)

(2.15)

Это система с трехдиагональной матрицей размерности :

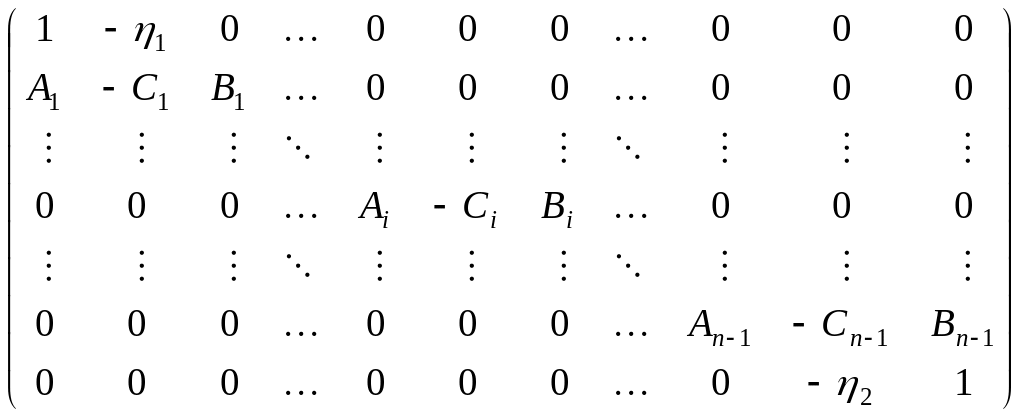
Для решения систем такого вида используется метод исключения неизвестных, называемый методом прогонки.

Пусть имеет место соотношение

(2.16)

с неопределенными коэффициентами

Подставим в (2.13), получаем

Сравнивая это тождество с (2.16), находим

(2.17)

(2.18)

Из (2.16) при и (2.14) получаем

(2.19)

Зная и переходя от к в формулах (2.17) и (2.18) можно определить для . Вычисление по формуле (2.16) ведутся путем перехода от к (т.е. зная можно найти ) и для начала этих вычислений необходимо знать . Определим из (2.15) и (2.16) при

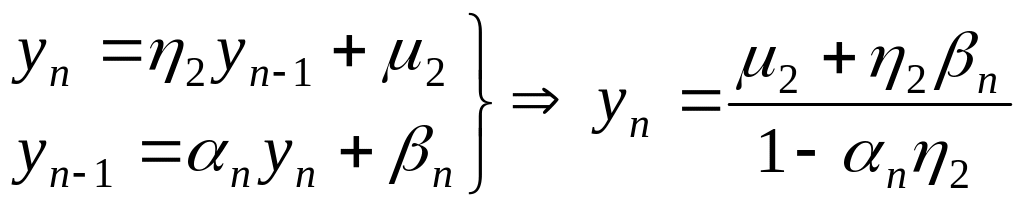(2.20)

Т.о., решение системы (2.13) –(2.15) методом прогонки, осуществляется по следующим формулам:

Прямой ход:

Обратный ход:

Условия устойчивости метода прогонки:

,

.

§3. Приближение функций эмпирическими формулами

При интерполировании используется условие равенства значений аппроксимирующей функции и данной функции в заданных точках – узлах интерполяции. Это означает, что значения функции в узлах должны быть заданы с высокой степенью точности. На практике часто возникает задача аппроксимации таблично заданной функции, значения которой известны приближенно. В этом случае используются другие способы аппроксимации. Наиболее распространенный из них метод наименьших квадратов.

П. 3.1. Подбор эмпирической формулы

В результате эксперимента была получена таблица значений: , . Требуется определить связь между исходными параметрами и искомой величиной на основе таблицы значений .

Задача состоит в том, чтобы найти такую функцию , значения которой при мало отличаются от опытных данных . Такая функция называется эмпирической формулой. График эмпирической зависимости, вообще говоря, не проходит через заданные точки . Это приводит к тому, что экспериментальные данные в некоторой степени сглаживаются, а интерполяционная формула повторила бы все ошибки, которые есть в исходных данных.

Построение эмпирической формулы состоит из двух этапов:

1. Подбор общего вида формулы.

2. Определение наилучших значений, содержащихся в формуле параметров.

Иногда общий вид формулы известен из физических или иных соображений. В других случаях вид может быть произвольным, предпочтение отдается наиболее простым формулам, которые могут выбираться из геометрических соображений, после нанесения экспериментальных точек на координатную плоскость и сравнение полученной кривой с графиками известных функций.

Простейшая эмпирическая формула (уравнение прямой) . О применимости этой формулы можно судить по величинам

.

Если , то формула применима.

В ряде случаев к линейной зависимости могут быть сведены экспериментальные данные, когда их график в декартовой системе координат не является прямой. Это может быть достигнуто путем введения новых переменных: . Они выбираются так, чтобы точки лежали на прямой. Такое преобразование называется выравниванием данных. Например, степенная зависимость логарифмированием преобразуется к виду .