Лекции по матану [2 курс]

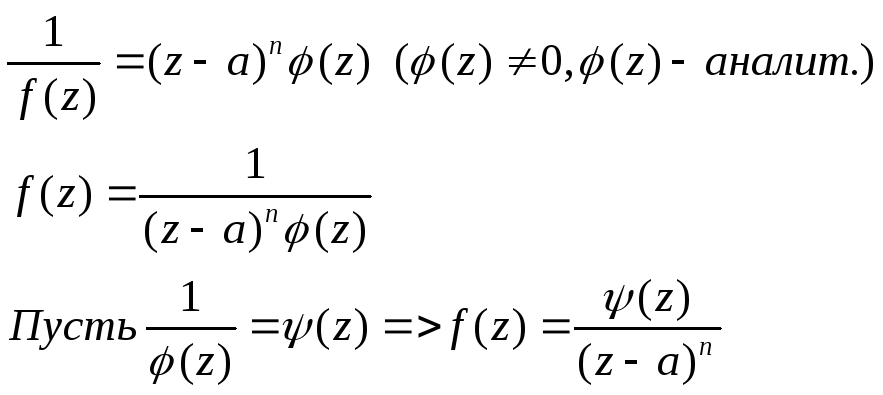
Точка а – полюс , когда f(z) можно представит в виде (см.вверх). т- порядок полюса.

Если а полюс порядка n для f(z) тогда и только тогда ,когда разложение в ряд Лорана в окрестности точки а содержит в главной части ровно n ненулевых членов.n<.

Точка а существенно особая точка функции f(z), если предел в этой точке не существует.

Точка а с.о.т. f(z), если главная часть ряда Лорана содержит бесконечное число членов отличных от 0

Рассмотри точку z= - особая точка.

Учитывая разложение в ряд Лорана при z=.

исследование идет через замену =1/z.

24-Вычет ФКП. Основная теорем о Выч.

Пусть точка а 0 правельная или изолированная особая точка f(z) однозначная ФКП и пусть С простой контур(обходящийся 1 раз в положительном направлении ) и такой, что функция f(z) является аналитичной на контуре и внутри за исключением быть может самой точки а=> тогда величину называют вычетом f(z) в точке а и обозначают Выч[f(z),a].

Теорема Основная о вычетах.

Пусть f(z) аналитичная функция вD за исключением изолирован-ных точек а₁,а₂,…,а_nD =>тогда для любого простого замкнутого контура C охватывающего все точки величина

по это формуле считаются контурные интегралы.

Доказательство: Пусть С – простойконтур на которой f(z)- аналитичная функция. Пусть внутри С f(z) аналитична, кроме точек а₁,а₂,…,а_n.

Проведем окружности С₁,С₂,…,С_n с центрами в точка а₁,а₂,…,а_n такчтобы окружности друг друга не касались. По теореме Коши для составного контура имеем.

25- Вычисление Вычетов.

Если точка а о.и. точка f(z),коэфициент

Вывод: Вычет это есть C_-1 коэффициент.

Выч[f(z),a]= C_-1.

Если точка а правльеная точка, то главной части в р.Л. нет, следует Выч[f(z),a]=0 для точки а (устранимой или правельной).

Если точка а- из.о. точка другого типа то вычит может быть любым полюсом.

Если а= то Выч[f(z),a]= -C_-1. Минус из-за обхода по часовой стрелке.

Теорема.

Пусть f(z) аналитич-на во всех точка плоскости за исключением a_N=, тогда

Доказательство.

Из сопоставления определения вычита в бесконечности и вычетов в конечной точке.

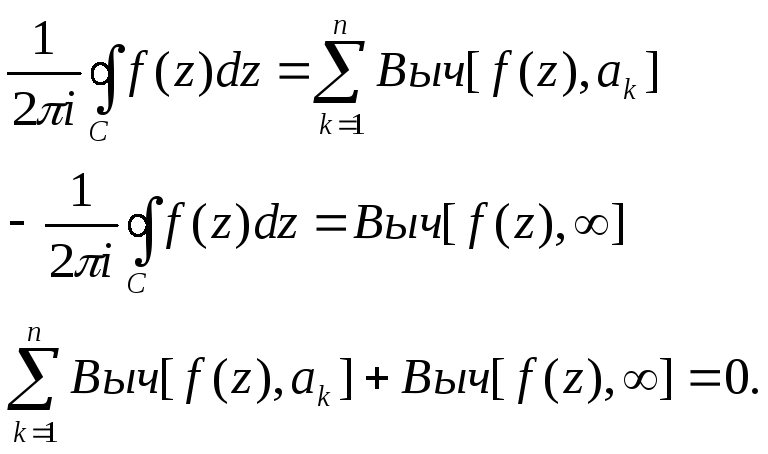
Утверждение.

Если функция f(z) имеет в точке z=a простой полюс, то вычет в этой точке равен

док-во

Т.к. а – простой полюс, то ряд Лорана имеет вид

-аналитическая функция в окрестности точки а.

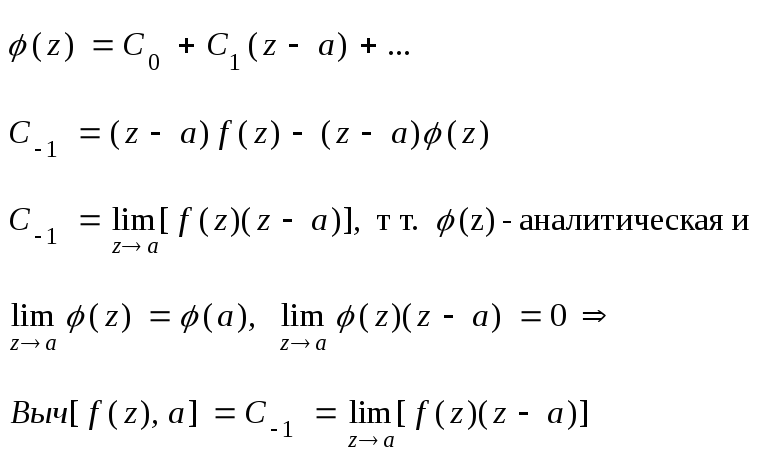Утверждение2.

Если функция f(z) имеет в точке z=а полюс порядка m, то вычет в этой точке равен

Доказательство:

Разложим в ряд Лорана

умножим на (z-a)^m

2-Последовательность…

Последовательность комплексных чисел называется пронумерованное бесконечное множество чисел.

Обозначение {Z_n}-последоват. Z_n –элемент послед.

Число Z называется пределом последовательности {Z_n}, если для >0 можно указать такой N(), начиная с которого все элементы Z_n этой последовательности удовлетворяют неравенству

|Z- Z_n|< при nN

Последовательность имеющая предел Z, называется сходящейся к числу Z, что записывается в виде:

Множество точек Z комплексной плоскости, лежащих внутри окружности радиуса  c центром в точке Z₀(|Z₀-Z|< ),называется -окреснтностью точки Z₀.

Теорема: Необходимыми и достаточными условиями сходимости последовательности {Z_n} является сходимость последовательностей действительных чисел a_n и b_n где (Z_n=a_n+ib_n)

Док-во: Если последовательность {Z_n}-> к числу Z=a+ib,то для >0 | a_n-a|| Z_n-Z|< и | b_n-b|< при nN(). Это доказывает сходимость последовательностей {a_n} и {b_n} к a и b обратное утверждение следует из соотношения :

где a и b является пределом последовательностей {a_n} и {b_n} и (Z=a+ib).

Последовательность {Z_n} называется ограниченной если существует такое положительное число М, что всех элементов Z_n этой последовательности имеет место неравенство | Z_n|<M.

Критерий Коши: Последовательность {Z_n} сходится тогда и только тогда, если для любого  можно указать такое N(), что |Z_n-Z_n+m|< при nN() и для любого т большего или равного нулю.

Доказательство: Необ. Крит.

Т.к. последовательность {Z_n} сходится, то сходится и последовательность действительных чисел {а_n}и{b_n}. Отсюда следует, что для >0 и любого номера т>0 |a_n-a_n+m|< /2 при nN₁() и|a_n-‑a_n+m|< /2 при nN₂().Выбираем из N₁ и N₂ наибольшее значение, в силу неравенства треугольника получаем |Z_n-Z_n+m|< при nN().

Дост.призн. Из соотношения |Z_n-Z_n+m|< при nN()следуют неравенства |a_n-a_n+m||Z_n-Z_n+m|< и |b_n-b_n+m||Z_n-Z_n+m|<, являющиеся достаточными условиями сходимости последовательностей {a_n} и {b_n}, т.е. сходимости последовательности {Z_n}. Тем самым доказано, что для сходимости {Z_n} с комплексными элементами необходимым и достаточным является критерий Коши.