
Курсовая работа - Разработка СУ для двухстепенного (двухзвенного) манипуляционного робота
.docМОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра управления и информатики в технических системах
![]()

по дисциплине:
«Автоматизированные ИСУ»
на тему:
«Разработка СУ для двухсцепного манипулятора».
Подготовила:
Студентка: Баронова О.О.
Заочного отделения, 5 курса
Специальность: 210100
Шифр: 603 609
Принял: Воронин Ю.Ю.
Москва
2008г.
Дано:
|
Последняя цифра шифра |
Масса звеньев |
Длина звеньев |
||
|
М1, кг |
М2, кг |
L1, м |
L2, м |
|
|
4 |
15 |
10 |
3 |
1,8 |

Часть 1. Уравнение динамики двух сцепного манипулятора.
Уравнение динамики в общем виде:
![]() .
.
 ,
где q – обобщенные координаты.
,
где q – обобщенные координаты.
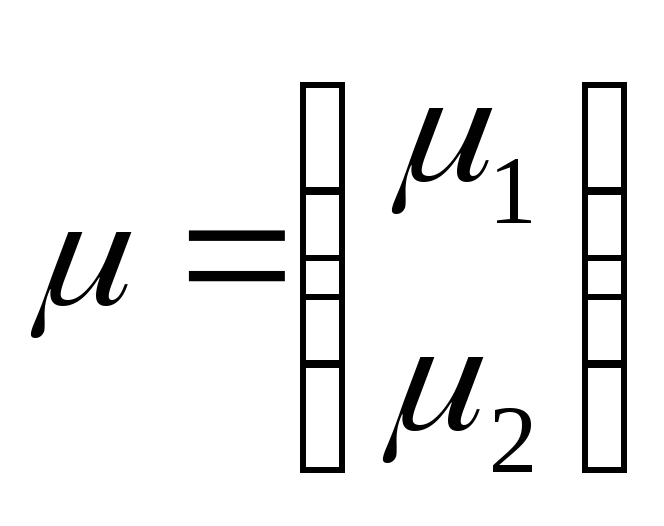 ,
где
,
где
![]() - управление.
- управление.
A(q) – матрица инерции манипулятора 2х2.
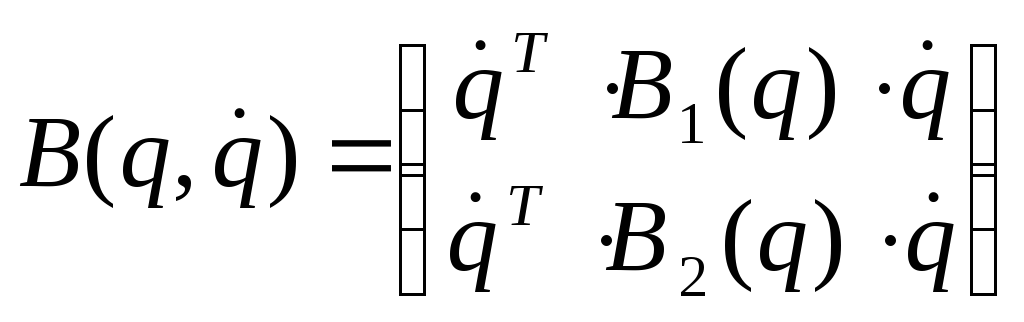 - моменты скоростных сил.
- моменты скоростных сил.
![]() - симметричные матрицы 2х2.
- симметричные матрицы 2х2.
Для А(q):
![]() ,
,
где
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Для матрицы
![]() :
:
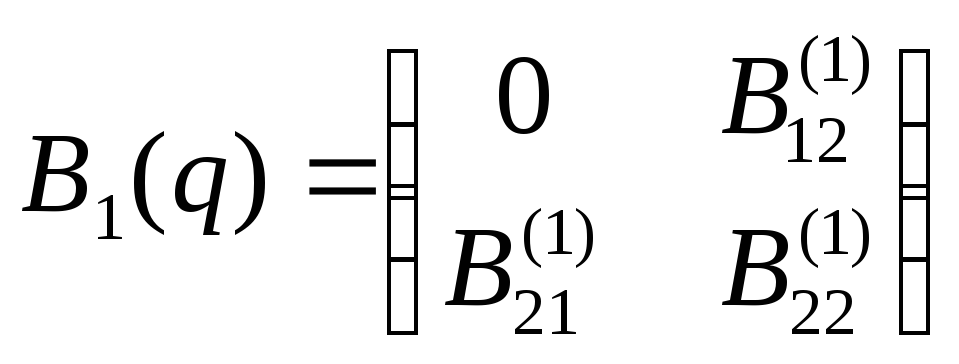 ,
,
![]() ;
;
![]() ;
;
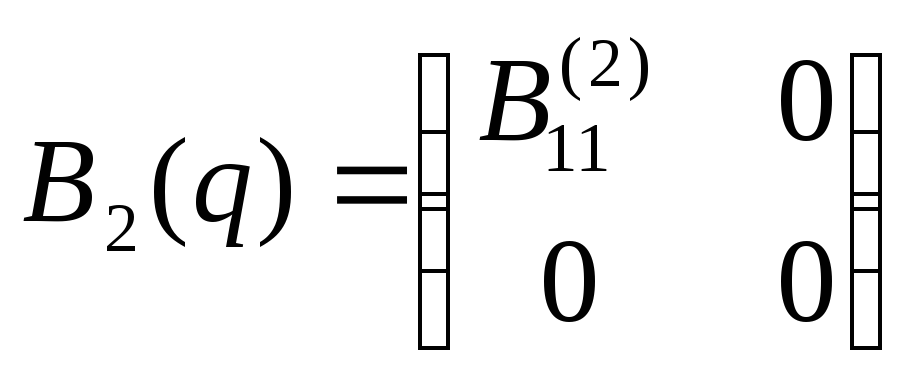 ,
,
![]() .
.
При расчете управления потребуются
собственные числа матриц
![]() :
:
![]() .
.
Их находят из уравнения:
![]() .
.
Эти числа должны быть вещественные, т. к. матрицы симметричные.
![]()
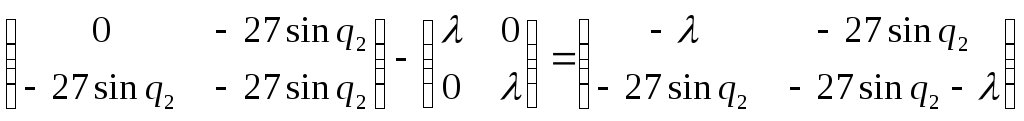 ;
;
![]()
![]() ;
;
![]() ;
;
![]() .
.
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Для матрицы
![]() :
:
![]() - гравитационные моменты.
- гравитационные моменты.
![]() ;
;
![]() ;
;
Здесь
![]() - ускорение свободного падения.
- ускорение свободного падения.

![]() .
.
Для дальнейших расчетов потребуются
частные производные от
![]() :
:
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Часть 2. Управление 2х степенным манипулятором с самонастройкой
по эталонной модели.
Требуется сформировать такое управление
![]() ,
при котором динамика манипулятора
описывалось бы уравнениями желаемой
модели вида:
,
при котором динамика манипулятора
описывалось бы уравнениями желаемой
модели вида:
![]() ,
,
здесь
![]() - заданная траектория движения манипулятора
в обобщенных координатах.
- заданная траектория движения манипулятора
в обобщенных координатах.
Управление
![]() ,
где uл – линейная
составляющая модели;
,
где uл – линейная
составляющая модели;
d – сигнал самонастройки.
![]() ,
где А0 – постоянная матрица
2х2,
,
где А0 – постоянная матрица
2х2,
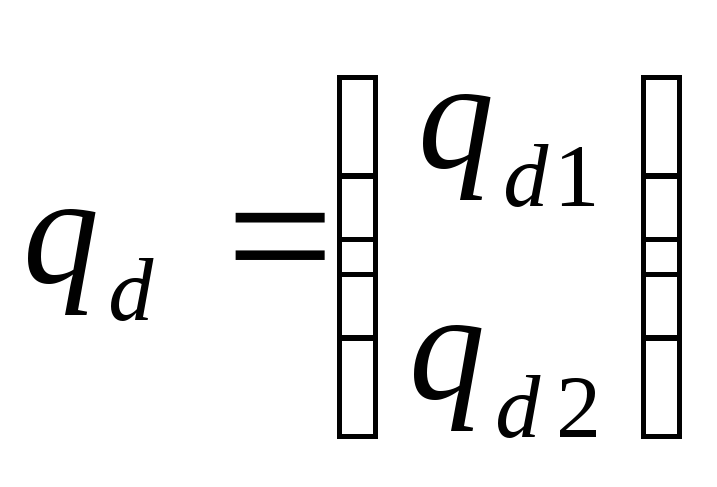 ,
KV
= const, K
= const – параметры желаемой
модели.
,
KV
= const, K
= const – параметры желаемой
модели.
В системе имеется эталонная модель:
![]() ,
где
,
где
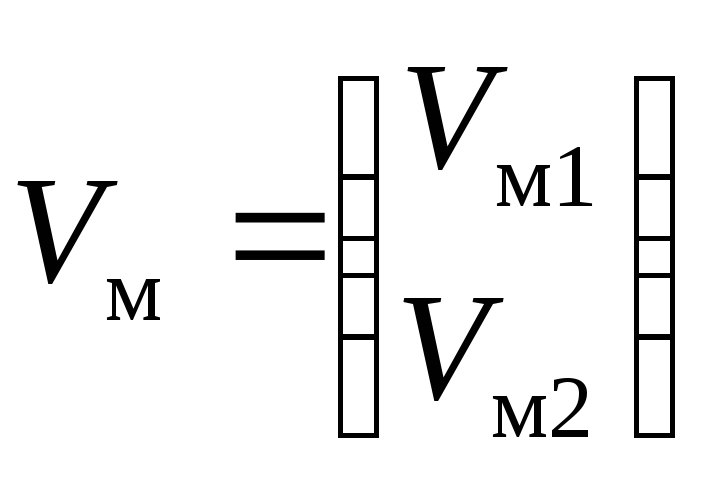 –
скорость эталонной модели.
–
скорость эталонной модели.
Ошибка системы относительно эталонной
модели:
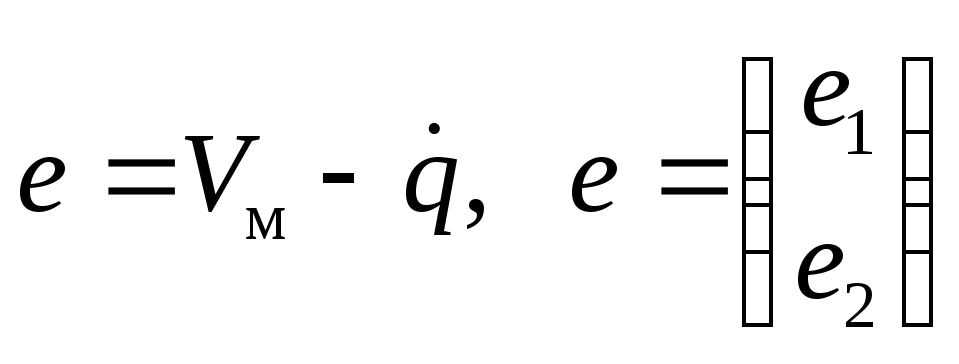 .
.
Для сигнала самонастройки:
![]() ;
;
![]() ;
;
![]() ;
;
![]() - ускорение эталонной модели;
- ускорение эталонной модели;
![]() ;
;
![]() ;
;
![]() .
.
Структурная схема самонастраивающейся системы.
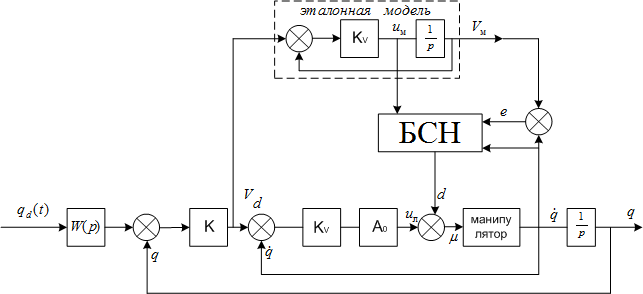
![]() .
.
Передаточная функция
![]() на структурной схеме вводится для
получения произвольных входных
воздействий
на структурной схеме вводится для
получения произвольных входных
воздействий
![]() и
и
![]() ,
и ввода их в систему управления. Когда
траектория
,
и ввода их в систему управления. Когда
траектория
![]() задается заранее, то можно вычислить
её первую и вторую производные заранее.
задается заранее, то можно вычислить
её первую и вторую производные заранее.
Часть 3. Расчет параметров системы (для расчетов используются
данные первой части).
Параметры K , KV
и
![]() рассчитывать не надо, они варьируются
в широких пределах. Остальные параметры
рассчитываются следующим образом:
рассчитывать не надо, они варьируются
в широких пределах. Остальные параметры
рассчитываются следующим образом:
1) Для первого положения манипулятора:
![]() .
.
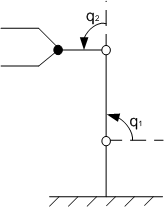
Для этого положения рассчитывается матрица инерции A(q), которая дает значение A0 .
Это положение манипулятора берется за номинальное.
![]() ;
;
![]() ;
;
![]() .
.
![]() .
.
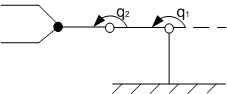
2) Для второго положения манипулятора:
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
![]() .
.
3) Матрицы
![]() ,
входящие в выражение для моментов
скоростных сил, рассчитываются для
первого положения манипулятора, т.к.
для второго положения они равны нулю:
,
входящие в выражение для моментов
скоростных сил, рассчитываются для
первого положения манипулятора, т.к.
для второго положения они равны нулю:
![]() ,
,
![]() .
.
4) Затем расчет ведется по формуле:
![]() .
.
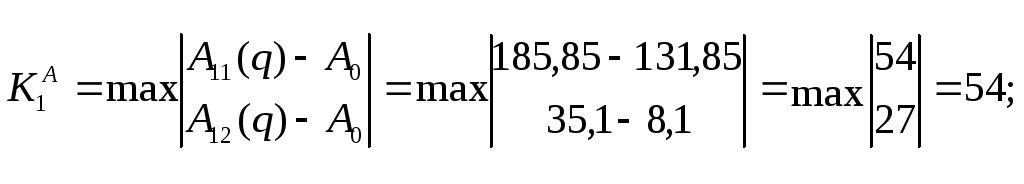
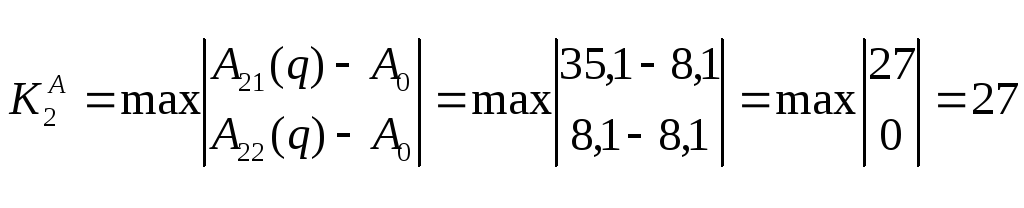 .
.
Результат представим в виде:
![]() .
.
5) Затем расчет ведется по формуле:
![]() .
.
Для дальнейших расчетов нам необходимо
получить точные значения собственных
чисел
![]() :
:
- для матрицы В1:
![]() ,
,
![]() ;
;
- для матрицы В2:
![]() ,
,
![]() ;
;
![]()
![]()
Результат представим в виде:
![]() .
.
6) Затем расчет ведется по формуле:
![]() .
.
Для вычисления
![]() надо рассчитать частные производные
по
надо рассчитать частные производные
по
![]() от гравитационных моментов
от гравитационных моментов
![]() .
Частные производные рассчитываются
для первого положения манипулятора,
так как для второго положения они равны
нулю.
.
Частные производные рассчитываются
для первого положения манипулятора,
так как для второго положения они равны
нулю.
Р
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Результат представим в виде:
![]() .
.
Ответ:
![]() .
.
![]() .
.
![]() .
.
