
Численные методы
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Выполнение лабораторного практикума по изучению численных методов предусматривается учебными планами следующих дисциплин: «Информатика и программирование», «Численные методы», «Моделирование систем». Лабораторные работы выполняются с целью приобретения практических навыков и закрепления теоретических знаний по указанным дисциплинам.
Лабораторные работы выполняются на ЭВМ с использованием языка программирования С. Для выполнения работ, учебная группа разбивается на подгруппы по 3-5 человек.
При подготовке к выполнению каждой работы студент должен:
изучить соответствующие разделы литературы, указанной в учебном плане;
ознакомиться с описанием лабораторной работы;
подготовить таблицы для записи результатов.
Проверка подготовки к выполнению очередной лабораторной работы осуществляется преподавателем при личном опросе. Если студент не знает содержания и методики проведения предстоящей лабораторной работы, то он не допускается к ее выполнению.
При выполнении лабораторной работы студент заполняет таблицы экспериментальных данных, производит необходимые расчеты, строит графики и подготавливает отчет о работе. Отчет выполняется по каждой работе отдельно. Студент защищает отчет после выполнения работы.
Лабораторная работа №1
ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
Цель работы: Приобретение навыков решения уравнений численными методами.
Задача решения
уравнения чаще всего встречаются при
изучении общетехнических и специальных
дисциплин, в инженерной практике.
Отыскать точное значение корня уравнения
можно лишь в некоторых частных случаях.
Кроме того, точное значение корня часто
все равно приходится заменить приближенным
(например, при решении уравнения
![]() ).
Поэтому при решении уравнения широко
используются методы позволяющие получать
приближенное решение с любой заданной
степенью точности.
).
Поэтому при решении уравнения широко
используются методы позволяющие получать
приближенное решение с любой заданной
степенью точности.
Пусть задано
уравнение
![]() ,
где функция
,
где функция
![]() определена и непрерывна на некотором
отрезке
определена и непрерывна на некотором
отрезке
![]() и имеет на нем непрерывную первую и
вторую производные
и имеет на нем непрерывную первую и
вторую производные
![]() и
и
![]() .
Корни заданного уравнения являются
нулями функции
.
Корни заданного уравнения являются
нулями функции
![]() и геометрически представленную собой
точки пересечения графика функции
с осью
и геометрически представленную собой
точки пересечения графика функции
с осью
![]() (рис. 1).
(рис. 1).
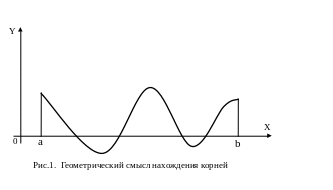
Решение задачи отыскания действительных корней заданного уравнения состоит из двух этапов:
а) Отделение (изоляция) корня, т.е. отыскание отрезка принадлежащего области определения функции , на котором имеется один и только один корень уравнения .
в) Вычисление или уточнение корня с заданной точностью.
Отделение корня уравнения основано на двух очевидных фактах:
1)На концах отрезка
функция имеет разные знаки, т.е.
![]()
![]() <
0. Очевидно, что при этом внутри отрезка
имеется, по крайней мере, один корень
уравнения
.
Однако это условие не гарантирует
существования единственного корня.
<
0. Очевидно, что при этом внутри отрезка
имеется, по крайней мере, один корень
уравнения
.
Однако это условие не гарантирует
существования единственного корня.
Например, на рис.1
>
0,
![]() <
0 т.е.
<
0, а внутри
имеется три корня.
<
0 т.е.
<
0, а внутри
имеется три корня.
2) На отрезке функция монотонна, т.е. ее производная не меняет знака на . Графически это обозначает, что либо возрастающая, либо убывающая.
Отделение корня можно производить аналитически или графически.
Графически корни уравнения можно отделить, построив график функции и приблизительно определив точки его пересечения с осью .
Аналитический
метод отделения корня состоит в том,
что вначале определяются интервалы
монотонности функции
,
т.е. интервалы в которых
![]() (путем решения уравнения
),
а затем вычисляют значения
на концах этих интервалов и определяют
интервал, на концах которого значение
имеют разные знаки. В результате может
получить так, что искомого интервала
не найдется. Это означает, что либо
уравнение
не имеет корня, либо корни являются
границами интервалов монотонности,
т.е. точками, в которых
(кратные корни).
(путем решения уравнения
),
а затем вычисляют значения
на концах этих интервалов и определяют
интервал, на концах которого значение
имеют разные знаки. В результате может
получить так, что искомого интервала
не найдется. Это означает, что либо
уравнение
не имеет корня, либо корни являются
границами интервалов монотонности,
т.е. точками, в которых
(кратные корни).
Собственно говоря,
любую точку с интервала, отделяющего
корень
![]() ,
можно считать приблизительным значением
корня поскольку ясно, что разность между
истинным значением корня
,
можно считать приблизительным значением
корня поскольку ясно, что разность между
истинным значением корня
![]() и его приближенным значением
и его приближенным значением
![]() ограничена величиной отрезка
ограничена величиной отрезка
![]() ,
т.е.
,
т.е.
![]() <
.
Если требуется более точное определение
корня, то необходимо изменить границы
интервала
таким образом, чтобы новый интервал был
меньше исходного и удовлетворял
приведенным выше условиям существование
корня.
<
.
Если требуется более точное определение
корня, то необходимо изменить границы
интервала
таким образом, чтобы новый интервал был
меньше исходного и удовлетворял
приведенным выше условиям существование
корня.
Для получения такого нового интервала используются различные методы последовательных приближений, позволяющие за несколько этапов сжатия исходного отрезка (итераций) получить интервал, длиной которого можно пренебречь.
М е т о д х о р д.
Идея метода состоит в том, что на отрезке
строится хорда
![]() ,
стягивающая концы дуги графика функции
,
и в качестве приближенного значения
корня выбирается число
,
являющееся абсциссой точки пересечения
хорды
с осью
(рис. 2).
,
стягивающая концы дуги графика функции
,
и в качестве приближенного значения
корня выбирается число
,
являющееся абсциссой точки пересечения
хорды
с осью
(рис. 2).
Для определения
числа
составим уравнение хорды, как прямой,
проходящей через две точки
![]() ,
,
![]()
Y
B
a
0
c b X
A
Рис.2
![]()
Положив
![]() ,
,
![]() получим
получим
![]()
После преобразований имеем две формулы
![]() ,
,
![]() .
.
Число
принимаем за первое приближение к
искомому корню и обозначим
![]() ,
,
![]() .
Очевидно, что если
не имеет знак на
,
точка
будет находится со стороны вогнутости
кривой
и разделит
на два отрезка
.
Очевидно, что если
не имеет знак на
,
точка
будет находится со стороны вогнутости
кривой
и разделит
на два отрезка
![]() и
и
![]() в одном из которых находится искомый
корень. Новый отрезок, отделяющий корень,
можно определить, сравнивая знаки
,
,
в одном из которых находится искомый
корень. Новый отрезок, отделяющий корень,
можно определить, сравнивая знаки
,
,![]() .
Из анализа рис. 3, на котором представлены
все возможные
.
Из анализа рис. 3, на котором представлены
все возможные
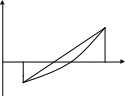
 Y
Y
Y A
B
a x1 b
0
b X a x1 B X
A
a) б)
Y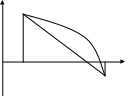
 Y B
Y B
A
a
x1 b
a X x1 b X
B A
в) г)
варианты поведения
функции
,
видно, что, если
![]() >0
(рис. 3а,в),отрезком, отделяющим корень
будет
,
в противном случае, т.е. при
<0
(рис. 3б,г), отрезком, отделяющим корень,
будет
.
>0
(рис. 3а,в),отрезком, отделяющим корень
будет
,
в противном случае, т.е. при
<0
(рис. 3б,г), отрезком, отделяющим корень,
будет
.
Повторяя такую же
процедуру на новом отрезке, определим
число
![]()
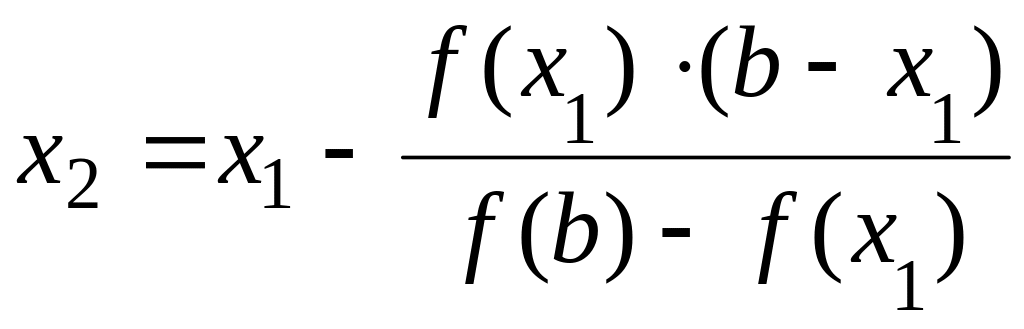 , при
>0;
, при
>0;
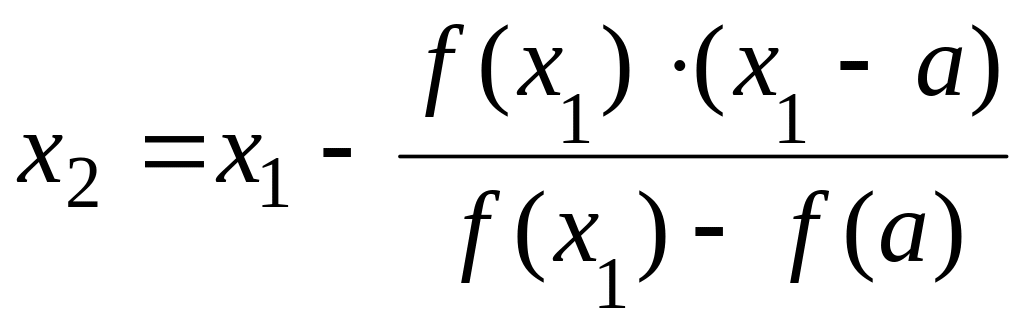 , при
<0.
, при
<0.
Затем аналогично
находим
![]() ,
,![]() и т.д. по итерационной формуле
и т.д. по итерационной формуле
![]() , при
>0;
, при
>0;
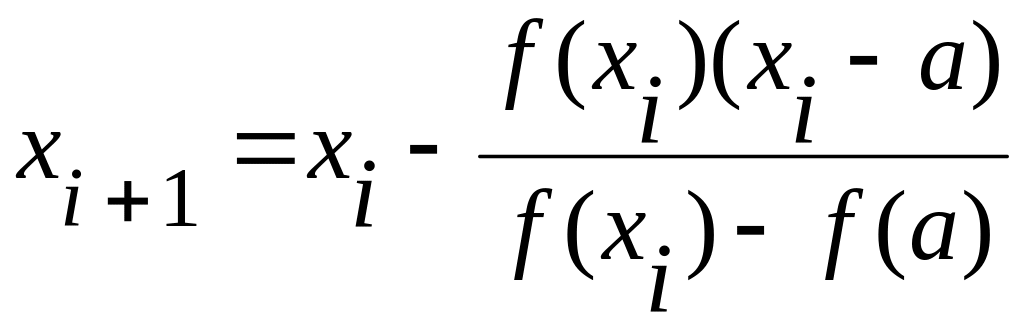 , при
>0.
, при
>0.
Процесс прекращаем
тогда, когда оценка полученного
приближения
![]() удовлетворяет заданной точности. Для
упрощения вычисления обычно задают
некоторые, достаточно малое число,
удовлетворяет заданной точности. Для
упрощения вычисления обычно задают
некоторые, достаточно малое число,
![]() и прекращаю вычисления, когда разность
между двумя последними приближениями
уменьшается меньше
и прекращаю вычисления, когда разность
между двумя последними приближениями
уменьшается меньше
![]() т.е.
т.е.
![]() .
Число
принимают за приближенное значение
корня уравнения
.
.
Число
принимают за приближенное значение
корня уравнения
.
М е т о д к а с а
т е л ь н ы х (Ньютона). Суть метода состоит
в том, что в одном из концов дуги
графика функции
проводится касательная к этой дуге и в
качестве приближенного значения
![]() выбирается число
являющееся абсциссой точки пересечения
этой касательной с осью
выбирается число
являющееся абсциссой точки пересечения
этой касательной с осью
![]() (рис.
4).
(рис.
4).
B
Y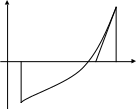
0 c b X
A
Рис. 4.
Как известно,
уравнение касательной к кривой
в точке
![]() имеет вид
имеет вид
![]() .
.
Следовательно,
уравнения касательных в точках
![]() и
и
![]() имеют вид
имеют вид
![]() ,
,
![]() .
.
Положив и определим абсциссу точки пересечения касательной с осью
![]() или
или
![]() .
.
Точка
будет первым приближением к корню,
поэтому обозначим ее
![]() .
Очевидно, что точка
.
Очевидно, что точка
![]() будет находиться со стороны выпуклости
кривой
.
Точка
разделит отрезок
на два отрезка
будет находиться со стороны выпуклости
кривой
.
Точка
разделит отрезок
на два отрезка
![]() и
и
![]() один из которых содержит корень. Если
один из которых содержит корень. Если
![]() ,
это будет отрезок
,
т.е. касательная проводится к точке
,
а при
,
это будет отрезок
,
т.е. касательная проводится к точке
,
а при
![]() получим отрезок
получим отрезок
![]() ,
т.е. касательная проводится к точке
.
Определив новый отрезок, повторим
процедуру, причем касательную проведем
в точке
,
т.е. касательная проводится к точке
.
Определив новый отрезок, повторим
процедуру, причем касательную проведем
в точке
![]() и получаем новую точку
и получаем новую точку
![]() .
.
Далее находим второе, третье и последующие приближения по итерационной формуле
![]() .
.
Процесс прекращается
тогда, когда разность между двумя
последними приближениями будет меньше
заданного числа
,
т.е.
![]() .
.
М е т о д с е к у щ и х. В методе касательных для нахождения каждого нового приближения корня необходимо вычислять не только значения функции , но и ее производную , что не всегда возможно, поскольку функция не обязательно должна быть задана в виде аналитического выражения. Например, может быть получена в результате решения какого-то дифференциального уравнения, или системы уравнений. Для преодоления этого препятствия можно заменить значения производной в методе касательных отношением конечных разностей в окрестности рассматриваемой точки, т.е. использовать приближенное равенство
![]() ,
,
где h – некоторая малая величина.
Геометрически это означает, что через рассматриваемую точку будет проводиться не касательная, а секущая (рис. 5).
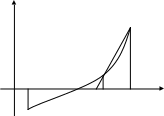 Y
Y
B
0 x* x x+h X
A
Рис. 5.
Поэтому данный метод называется методом секущих. Итерационная формула будет аналогична методу касательных
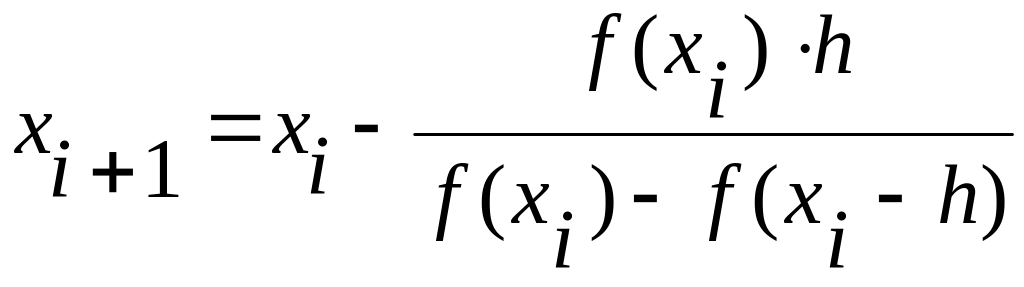 .
.
При использовании
этого метода следует уменьшать величину
![]() по мере приближения к корню.
по мере приближения к корню.
М е т о д п р о с
т ы х и т е р а ц и й . Рассмотрим
уравнение
![]() .
Это уравнение может быть получено из
уравнения
путем прибавления к обоим членам
и заменой
.
Это уравнение может быть получено из
уравнения
путем прибавления к обоим членам
и заменой
![]() ,
т.е. корень уравнения
совпадает с корнем уравнения
.
,
т.е. корень уравнения
совпадает с корнем уравнения
.
Пусть
- отрезок, отделяющий корень
,
т.е.
![]() .Выберем
произвольную точку
.Выберем
произвольную точку
![]() и вычислим значение
и вычислим значение
![]() в этой точке
в этой точке
![]() .
.
По найденному значению построим вторую точку и т.д. по формуле
![]() .
.
Если полученная
таким образом последовательность
сходится, то она сходится к корню
,
т.е.
![]() и за конечное число итераций можно
получить приближенное значение корня
с заданной точностью
,
т.е.
и за конечное число итераций можно
получить приближенное значение корня
с заданной точностью
,
т.е.
![]() .
Однако описанный итерационный процесс
не всегда сходится.
.
Однако описанный итерационный процесс
не всегда сходится.
Рассмотрим
геометрический смысл процесса и его
сходимость. Корень уравнения
,
это точка пересечения прямой
![]() и
графика функции
и
графика функции
![]() (рис. 6). Абсцисса
получена пересечением прямых
(рис. 6). Абсцисса
получена пересечением прямых
![]() и
.
Абсцисса
получается пересечением прямых
и
.
Абсцисса
получается пересечением прямых
![]() и
и т.д.
и
и т.д.
Y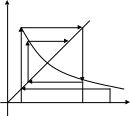
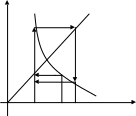
Y
0 x1 x2 x0 X 0 x1 x0 x2 X
а) б)
Рис. 6
На рис. 6а видно,
что последовательность
![]() сходится к
,
а на рис. 6б – расходится. Сходимость
процесса зависит от угла наклона линии
,
т.е. от значения
сходится к
,
а на рис. 6б – расходится. Сходимость
процесса зависит от угла наклона линии
,
т.е. от значения
![]() .
Если
.
Если
![]() ,
,
![]() ,
то процесс сходится, при
,
то процесс сходится, при
![]() ,
процесс расходится и при
,
процесс расходится и при
![]() ,
процесс может как сходиться, так и
расходиться.
,
процесс может как сходиться, так и
расходиться.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Ознакомиться с методами приближенного вычисления корней уравнений.
В соответствии с вариантом разработать программу на языке С.
С помощью дополнительных программ отделить наименьший по модулю корень заданного уравнения. Вариант задания выбрать из табл. 1.
Вычислить с помощью программы значение отдельного корня четырьмя различными методами. При использовании метода простых итераций найти решение при разных начальных приближениях. Результаты вычислений занести в табл.2.
Таблица 1
№ |
Вид функции |
№ |
Вид функции |
1 |
|
11 |
|
2 |
|
12 |
|
3 |
|
13 |
|
4 |
|
14 |
|
5 |
|
15 |
|
6 |
|
16 |
|
7 |
|
17 |
|
8 |
|
18 |
|
9 |
|
19 |
|
10 |
|
20 |
|
Таблица 2
1 |
Метод 1 |
Метод 2 |
Метод 3 |
Метод 4 |
Метод 5 |
|||||
xi |
yi |
xi |
yi |
xi |
yi |
xi |
yi |
xi |
yi |
|
1 2 . . . |
|
|
|
|
|
|
|
|
|
|
ОТЧЕТ О РАБОТЕ
Отчет должен содержать:
График исследуемой функции с интервалами отделения корней.
Таблицы пошаговых расчета корня уравнения.
Обоснованное заключение о преимуществах и недостатках использования исследованных методов решения применительно к заданному уравнению.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Как и зачем выполняется отделение корня?
Каково условие сходимости метода хорд?
Чем отличаются итерационные методы хорд и секущих?
Какие методы предпочтительнее воспользоваться для решения уравнений
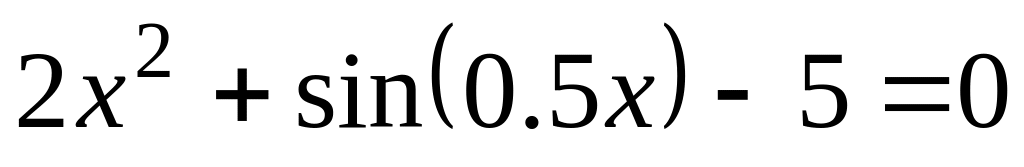 ,
,
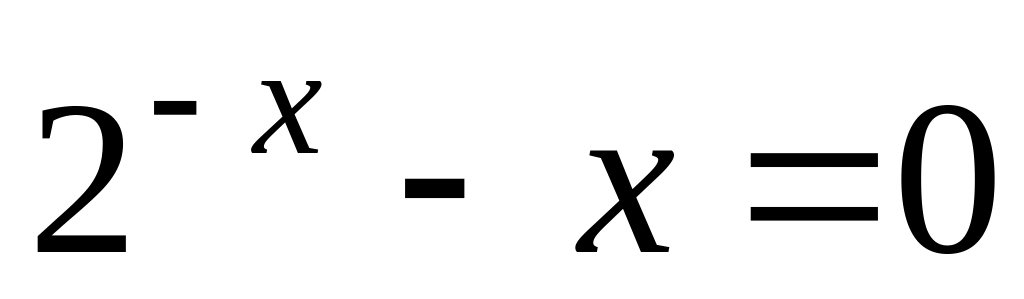 ?
?В чем заключается условие сходимости метода простых итераций?
В чем отличие методов касательной и секущей, и что у них общего?
ЛИТЕРАТУРА [1, c. 451-473]; [3, c. 112-157]; [5, c. 170-210]; [6, c. 86-116].
