
- •Определение вязкости воздуха методом истечения из капилляра
- •Определение вязкости воздуха методом истечения из капилляра
- •660014, Г.Красноярск, просп. Им. Газ. «Красноярский рабочий», 31.
- •Определение вязкости воздуха методом истечения из капилляра
- •Краткие теоретические сведения
- •Метод исследования
- •Описание установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Библиографический список
Федеральное агентство по образованию
Сибирский государственный аэрокосмический университет
имени академика М.Ф. Решетнева
Определение вязкости воздуха методом истечения из капилляра
Методические указания к выполнению лабораторной работы
по разделу физики «Молекулярная физика» для студентов технических специальностей очной формы обучения
Красноярск 2010
УДК 535.12(075)
Рецензент
доктор физико-математических наук, профессор С.А. Аплеснин
(Сибирский государственный аэрокосмический
университет имени академика М.Ф. Решетнева)
Печатается по решению методической комиссии ИКТ
Определение вязкости воздуха методом истечения из капилляра: метод. указания к выполнению лабораторной работы по разделу физики «Молекулярная физика» для студентов тех. спец. очной формы обучения / сост.: Н.В. Филенкова, А.Ю. Власов; Сиб. гос. аэрокосмич. ун-т. – Красноярск, 2010. – 18 с.
Учебно-методическое издание
Определение вязкости воздуха методом истечения из капилляра
Методические указания к выполнению лабораторной работы
по разделу физики «Молекулярная физика» для студентов
технических специальностей очной формы обучения
Составители
Филенкова Нина Викторовна, Власов Антон Юрьевич,
Редактор А.А. Ловчикова
Оригинал-макет и верстка А.А. Ловчиковой
Подп. в печать . Формат 6084/16. Бумага офсетная.
Печать плоская. Усл. печ. л. 1,2. Уч.-изд. л. 1,25.
Тираж 100 экз. Заказ С 249.
Санитарно-эпидемиологическое заключение
№ 24.49.04.953.П.000032.01.03 от 29.01.2003 г.
Редакционно-издательский отдел Сиб. гос. аэрокосмич. ун-та.
Отпечатано в отделе копировально-множительной техники
Сиб. гос. аэрокосмич. ун-та
660014, Г.Красноярск, просп. Им. Газ. «Красноярский рабочий», 31.
Сибирский государственный аэрокосмический
университет имени академика М.Ф. Решетнева, 2010
Лабораторная работа 20
Определение вязкости воздуха методом истечения из капилляра
Цель работы: Изучить явление вязкости газов и одного из методов определения коэффициента вязкости газов. Определить коэффициент динамической вязкости воздуха, числа Рейнольдса и длины свободного пробега молекул по полученным данным.
Приборы и принадлежности: Компрессор, баллон, секундомер, манометр.
Краткие теоретические сведения
Вязкость (внутреннее трение) – свойство газов, жидкостей и твердых тел сопротивляться их течению, возникающему под действием внешних сил. Количественной характеристикой этого свойства является коэффициент вязкости (коэффициент внутреннего трения). Вязкость газов согласно молекулярно-кинетической теории объясняется следующим образом. При направленном движении газа (например, в трубе) молекулы газа участвуют одновременно в двух движениях: хаотическом тепловом и направленном. Молекулы, оказавшиеся вблизи стенки, сталкиваются со стенкой, теряют свою энергию и замедляются.
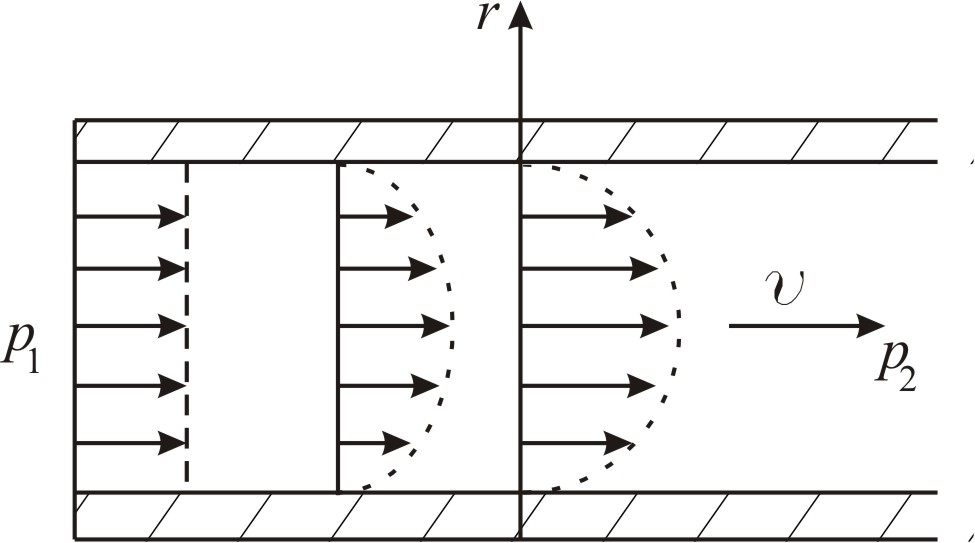
Рис. 1. Распределение скоростей по сечению трубы
За счет теплового движения они переходят в близлежащие слои газа и замедляют их. Вследствие этого скорости направленного движения молекул оказывается различными в разных точках поперечного сечения трубы (рис. 1).
При
ламинарном
течении поток газа движется как бы
слоями, не перемешивающимися друг с
другом, и в пределах слоя скорость
направленного движения остается
постоянной. Для цилиндрической трубы
круглого сечения на некотором расстоянии
от конца трубы устанавливается
стационарное распределение скоростей
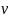 по параболическому закону
по параболическому закону
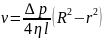 , (1.1)
, (1.1)
где p – перепад давления на концах трубы, l – длина трубы, R – ее радиус , r – радиальная координата (рис. 1), ‑ коэффициент динамической вязкости.
Физический смысл коэффициента динамической вязкости можно определить из закона Ньютона для силы внутреннего трения
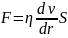 ,
(1.2)
,
(1.2)
где
F
– модуль силы взаимодействия между
двумя соседними слоями с площадью
соприкосновения S,
величина
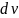 /dr
‑ называемая градиентом скорости
для одномерного случая, показывает
изменение скорости течения на единице
длины при переходе от слоя к слою в
радиальном направлении (рис. 2.). Из
формулы (1.2) можно выразить коэффициент
динамической вязкости:
/dr
‑ называемая градиентом скорости
для одномерного случая, показывает
изменение скорости течения на единице
длины при переходе от слоя к слою в
радиальном направлении (рис. 2.). Из
формулы (1.2) можно выразить коэффициент
динамической вязкости:
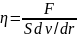 , (1.3)
, (1.3)
откуда следует, что коэффициент динамической вязкости, зависящий от природы газа, численно равен силе взаимодействия между слоями газа, действующей на единицу площади их соприкосновения при градиенте скорости, равном единице. Единица вязкости в СИ обозначается Нс/м2.
Все сказанное относится и к жидкостям, и к газам. Для жидкостей и газов существенно различен характер зависимости вязкости от температуры. У жидкостей коэффициент вязкости сильно уменьшается с повышением температуры. У газов, наоборот, коэффициент вязкости с температурой растет. Это отличие является следствием различного механизма внутреннего трения в жидкостях и газах.
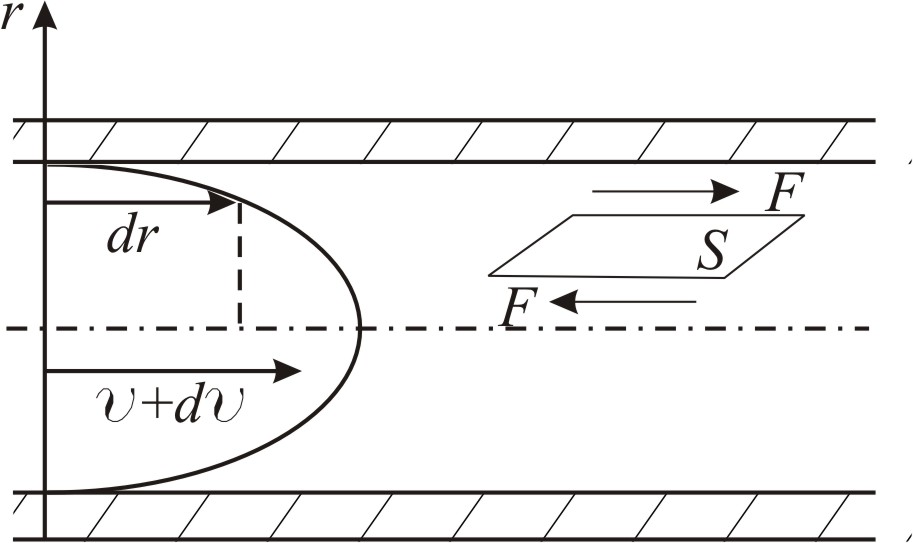
Рис.2. Сила внутреннего трения
Если перепад давления увеличивается, скорость течения растет и движение газа из ламинарного переходит в турбулентное, при котором скорости частиц в каждом данном месте изменяются беспорядочным образом, слои перемешиваются и образуются завихрения (рис. 3).
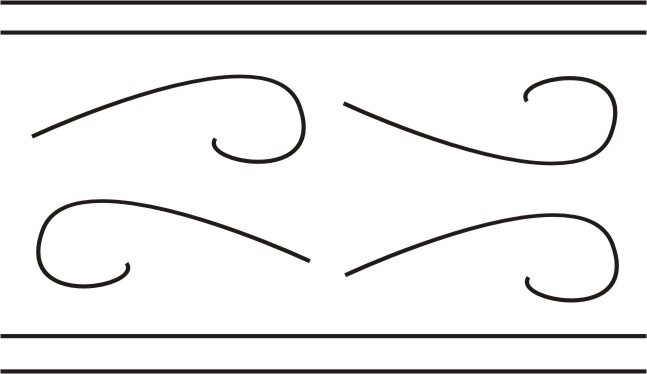
Рис. 3. Турбулентное движение
Для оценки изменения характера движения газа (жидкости) используют безразмерную величину, называемую числом Рейнольдса
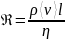 ,
(1.4)
,
(1.4)
где
ρ ‑ плотность среды,
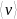 ‑ средняя скорость течения, l
‑
характерный для поперечного сечения
размер, например сторона квадрата при
квадратном сечении, радиус или диаметр
при круглом сечении.
‑ средняя скорость течения, l
‑
характерный для поперечного сечения
размер, например сторона квадрата при
квадратном сечении, радиус или диаметр
при круглом сечении.
При малых значениях числа Рейнольдса наблюдается ламинарное течение. Начиная с некоторого определенного значения Re, называемого критическим, течение приобретает турбулентный характер. При движении газа в круглой трубе течение является ламинарным, если число Рейнольдса Re 1000.
В число Рейнольдса входят в виде отношения две величины, зависящие от свойств жидкости, плотность ρ и коэффициент вязкости . Отношение
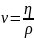 (1.5)
(1.5)
называется кинематической вязкостью. Используя кинематическую вязкость, число Рейнольдса можно записать как
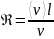 . (1.6)
. (1.6)
Число Рейнольдса может служить критерием подобия для течения жидкостей в трубах и т.д. Характер течения различных жидкостей (или газов) в трубах разных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же значение Re.
Если газ считать идеальным, то из молекулярно-кинетической теории можно получить выражение для коэффициента динамической вязкости
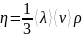 (1.7)
(1.7)
где
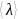 ‑ средняя длина свободного пробега
молекул, т.е. среднее расстояние, которое
проходит молекула между двумя
последовательными столкновениями с
другой молекулой;
‑ средняя длина свободного пробега
молекул, т.е. среднее расстояние, которое
проходит молекула между двумя
последовательными столкновениями с
другой молекулой;
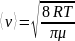 ‑
средняя арифметическая скорость
теплового движения молекул, R
‑ универсальная газовая постоянная,
μ ‑ молярная масса газа, Т
– абсолютная температура газа.
‑
средняя арифметическая скорость
теплового движения молекул, R
‑ универсальная газовая постоянная,
μ ‑ молярная масса газа, Т
– абсолютная температура газа.
