17. Экстремали с изломами. Условия Вейерштрасса - Эрдмана.

Рассмотрим простейшую задачу с фиксированными граничными точками и 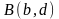. Будем считать, что минимум рассматриваемого интегрального функционала достигается на кривой , которая проходит через эти точки и имеет один излом в точке 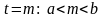. При этом её левая ветвь и правая ветвь – непрерывно дифференцируемые функции на отрезках 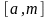и 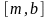соответственно. Ветви кривой являются экстремалями, т.е. принадлежат двухпараметрическому семейству , представляющему общее решение уравнения Эйлера. Следовательно, их уравнения имеют вид

и отличаются только значениями двух постоянных и с краевыми условиями

Дополнительное необходимое условие достижения экстремума функционала в точке в данной задаче представляется в виде:

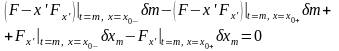
для любых достаточно малых по модулю приращений (вариаций) и , здесь и – координаты точки излома . В свою очередь, для выполнения этого условия необходимо и достаточно, чтобы выполнялись два равенства:

Полученные равенства (их принято называть условиями Вейерштрасса-Эрдмана), представляют собой дополнительные необходимые условия, которым должна удовлетворять кривая и координаты точки её излома, обеспечивающие минимум интегрального функционала.

Если кривая заранее не известна, то полученные условия являются дополнительными соотношениями для поиска неизвестны и .

18. Простейшие задачи с ограничениями. Условия в точках сопряжения экстремалей и границ.

Как и ранее, рассмотрим интегральный функционал

,

где подынтегральная функция является дважды непрерывно дифференцируемой на множестве , а также множество функций

, где – заданные числа, – заданная непрерывно дифференцируемая функция.

Существо задачи с ограничениями состоит в поиске функции , для которой функционал принимает наименьшее значение по отношению к другим функциям из множества .

Если известна кривая , решающая задачу, то она может состоять только из отрезков экстремалей и отрезков кривой – границы запретной области. Пусть кривая , решающая задачу с ограничениями, состоит только из двух участков: экстремали , , 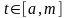и отрезка границы , . При этом предполагаем, что граничная кривая проходит через правую крайнюю точку . Т.к. функция является экстремалью, т.е. входит в двухпараметрическое семейство решений уравнения Эйлера, то она удовлетворяет следующим граничные условиям:

(****)где – точка сопряжения.

В данной задаче дополнительное необходимое условие экстремума имеет вид: .Иными словами, в регулярной ситуации сопряжение экстремали с граничной кривой должно быть с необходимостью гладким.

Таким образом, если кривая , решающая задачу с ограничением, заранее не известна, то равенства (****) совместно с условием 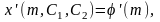дают систему из трёх нелинейных уравнений с тремя неизвестными и для ее нахождения. Решение этой системы позволяет получить допустимую экстремаль в задаче с ограничениями, на которой, совместно с участком границы, может достигаться экстремум.