11 . Основные леммы классического вариационного исчисления (Лагранжа, Дюбуа-Реймона).

Лемма 1 (Лемма Лагранжа).  Пусть известно, что 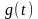– непрерывная функция: 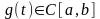. Тогда, если для любой функции 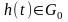выполняется равенство

,

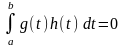то имеет место тождество ( ).

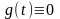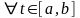Лемма 2 (Лемма Дюбуа-Реймона).  Пусть известно, что – непрерывная функция: . Тогда, если для любой функции выполняется равенство

,

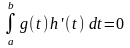то имеет место тождество ( ).

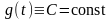12 . Уравнение Эйлера (в двух формах).

Теорема 1.  Если функция – точка слабого локального (относительного) экстремума функционала на множестве , то существует первая вариация функционала на множестве

, ,

причём везде на она обращается в нуль: .

Следствие.  Если – функция, обеспечивающая экстремум функционала на множестве , то она удовлетворяет условию

. (*)

Условие (*) может быть преобразовано с использованием леммы Лагранжа вариационного исчисления к следующему виду.

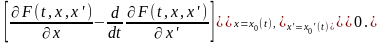
При этом на функцию накладывается дополнительное ограничение, т.е. предполагается, что она дважды непрерывно дифференцируемая на отрезке , т.е. имеет там непрерывную вторую производную: .

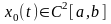Если функция заранее не задана, то полученное соотношение можно трактовать, как уравнение для её поиска, которое принято записывать в виде

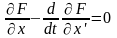
и называть уравнением Эйлера в дифференциальной форме.

Без введения каких-либо дополнительных предположений о свойствах функции с помощью леммы Дюбуа-Реймона условие (*) может быть приведено к виду:

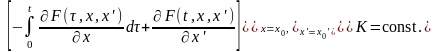
Если функция заранее не задана, то указанное соотношение можно трактовать, как уравнение для её поиска, которое принято записывать в виде

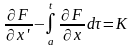
и называть уравнением Эйлера в интегро-дифференциальной форме.

13 Экстремали в регулярном и сингулярном случаях. Теорема Гильберта

Определение 1.  Любая функция 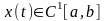, удовлетворяющая уравнению Эйлера, сформированному для интегрального функционала 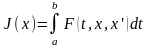, называется экстремалью по отношению к этому интегральному функционалу. Если эта функция ещё и принадлежит множеству , т.е. удовлетворяет краевым условиям 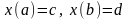, то она называется допустимой экстремалью по отношению к простейшей основной задаче.

В связи с приведенным определением и на основании сформулированного необходимого условия экстремума можно утверждать, что любое решение простейшей основной задачи является допустимой экстремалью. Обратное утверждение не верно: допустимая экстремаль не обязательно обеспечивает экстремум функционала в простейшей задаче.

Экстремали в регулярном и в сингулярном случае

Определение 2.  Точку 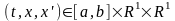будем называть регулярной точкой по отношению к интегральному функционалу 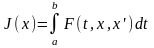, если имеет место условие

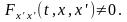
Определение 3.  Экстремаль будем называть регулярной экстремалью по отношению к интегральному функционалу (для интегрального функционала) , если для любого значения 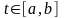точки 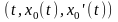являются регулярными, т.е.

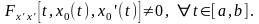
Теорема 2 (Теорема Гильберта о регулярной экстремали).  Если функция – регулярная экстремаль для функционала , то она имеет непрерывную вторую производную на отрезке , т.е. .

Определение 4.  Будем говорить, что в вариационной задаче имеет место регулярная ситуация если подынтегральная функция интегрального функционала такова, что

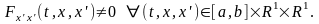
Пусть в рассматриваемой в данной главе простейшей основной задаче имеет место регулярная ситуация. Тогда в уравнении Эйлера, представленном в форме

,

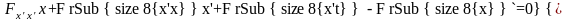коэффициент при второй производной ненулевой, т.е. в этом случае уравнение Эйлера – это нелинейное дифференциальной уравнение второго порядка.

Регулярность ситуации позволяет привести указанное уравнение к виду

, (**)

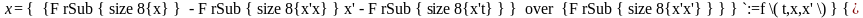где функция 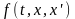непрерывна по совокупности своих переменных.

Существование экстремалей определяется условиями существования и единственности решения задачи Коши для дифференциального уравнения второго порядка (**). Как известно, общее решение дифференциального уравнения (**) второго порядка может быть представлено в виде

,

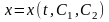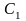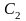где и – произвольные вещественные постоянные.

Для простейшей задачи эти постоянные должны быть определены из краевых условий

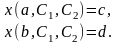
Данные соотношения составляют нелинейную систему из двух уравнений с двумя неизвестными и . Если система имеет хотя бы одно решение 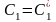, , 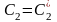то для уравнения Эйлера (**) существует допустимая экстремаль .

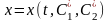Определение 5.  Простейшая основная задача называется сингулярной (или вырожденной), если подынтегральная функция интегрального функционала такова, что имеет место равенство .

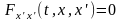Очевидно, что указанная ситуация имеет место, если функция 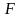зависит от переменной 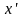линейно (в частности – вообще не зависит), т.е.

,

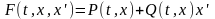где 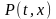и 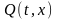– дважды непрерывно дифференцируемые функции по совокупности своих аргументов и в данном случае уравнение Эйлера принимает вид

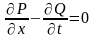, откуда следует, что оно не является дифференциальным