
- •4 Понятие функционала. Функционалы в метрических и линейных пространствах
- •5Формализованные задачи вариационного исчисления. Пространство : норма, метрика, близость элементов. Классификация экстремумов.
- •6. Элементы дифференциального исчисления в л н п: производная по направлению, первая вариация функционала
- •7. Элементы дифференциального исчисления в л н п:дифференцируемость по Гато и Фреше. Дифференциал Фреше линейного непр функционала
- •8 Сильна дифференцируемость функционала
- •9 Условие локального экстремума функционалов
- •10. Простейшая основная задача вариационного исчисления. Необходимое условие экстремума.
- •11 . Основные леммы классического вариационного исчисления (Лагранжа, Дюбуа-Реймона).
- •12 . Уравнение Эйлера (в двух формах).
- •13 Экстремали в регулярном и сингулярном случаях. Теорема Гильберта
- •Экстремали в регулярном и в сингулярном случае
- •14. Случаи упрощения уравнений Эйлера. Примеры
- •15. Простейшая вариационная задача с подвижными границами. Выражение для дифференциала по параметру.
- •16. Простейшая задача с подвижными границами. Необходимые условия экстремума для случая свободных границ и условия трансверсальности
- •17. Экстремали с изломами. Условия Вейерштрасса - Эрдмана.
- •18. Простейшие задачи с ограничениями. Условия в точках сопряжения экстремалей и границ.
- •19. Вторая вариация функционала. Необходимое условие Лежандра.
- •20. Достаточные условия слабого относительного экстремума.
- •3 Примеры содержательных задач о поиске экстремума интегрального функционала
6. Элементы дифференциального исчисления в л н п: производная по направлению, первая вариация функционала
ЛИНЕЙНЫМ МЕТРИЧЕСКИМ ПРОСТРАНСТВОМ (ЛМП) называется линейное пространство, в котором каким-либо способом введена метрика, инвариантная относительно сдвига, т.е.

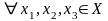 .
.
НОРМИРОВАННЫМ ПРОСТРАНСТВОМ называется линейное пространство, в котором каждому элементу поставлено в соответствие неотрицательное число – норма элемента
Определение: приращением ;
Предположим, что приращение функционала можно представить в виде где - линейный по отношению к функционал, а
Определение: Величина , т.е. главная, линейная по отношению к часть приращения функционала называется вариацией функционала и обозначается
Будем далее рассматривать линейное нормированное метрическое пространство , на котором задан функционал .
ОПРЕДЕЛЕНИЕ 1.
Производной по направлению
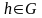 функционала
в точке
функционала
в точке
 называется предел (если он существует)
называется предел (если он существует)
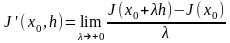 .
.
Заметим, что производная
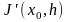 является числом.
является числом.
ОПРЕДЕЛЕНИЕ 2.
Если для некоторой фиксированной точки
для функционала
существует производная
по любому направлению
,
то функционал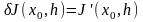 ,
,
определённый на множестве
элементов
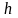 называется первой вариацией функционала
в точке
называется первой вариацией функционала
в точке
 :
говорят, что в этой точке функционал
имеет первую вариацию.
:
говорят, что в этой точке функционал
имеет первую вариацию.
ОПРЕДЕЛЕНИЕ 3: Если
в точке
функционал
имеет первую вариацию,
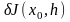 ,
удовлетворяющую равенству
,
удовлетворяющую равенству
 ,
,
 ,
,
или, что то же самое, если существует
предел ,
,
,
,
то говорят, что в этой точке функционал имеет первую вариацию в смысле Лагранжа (по Лагранжу).
Примеры
Для функционала
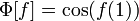 вещественной
функции вещественного аргумента — для
любой
вещественной
функции вещественного аргумента — для
любой 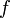 и
и 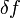 будет
верным
будет
верным 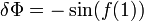 .
.Для функционала
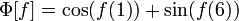 вещественной
функции вещественного аргумента — для
любой
и
будет
верным
вещественной
функции вещественного аргумента — для
любой
и
будет
верным 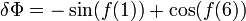 .
.Для функционала
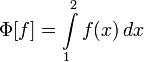 вещественной
функции вещественного аргумента — для
любой
и
будет
верным
вещественной
функции вещественного аргумента — для
любой
и
будет
верным 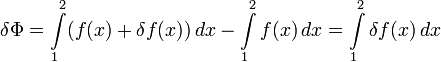 .
.
Примеры
(Здесь не вводится специальных обозначений для производной по направлению.)
Производная функционала
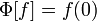 в
точке
в
точке 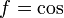 по
направлению
по
направлению 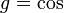 равна
равна 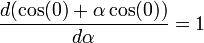 .
.Производная функционала в точке по направлению
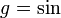 равна
равна 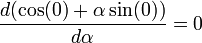 .
.
7. Элементы дифференциального исчисления в л н п:дифференцируемость по Гато и Фреше. Дифференциал Фреше линейного непр функционала
ЛИНЕЙНЫМ МЕТРИЧЕСКИМ ПРОСТРАНСТВОМ (ЛМП) называется линейное пространство, в котором каким-либо способом введена метрика, инвариантная относительно сдвига, т.е.
.
НОРМИРОВАННЫМ ПРОСТРАНСТВОМ называется линейное пространство, в котором каждому элементу поставлено в соответствие неотрицательное число – норма элемента
Определение 4. Если в точке функционал имеет первую вариацию , которая является линейным и непрерывным по переменной функционалом, то говорят, что в этой точке функционал является слабо дифференцируемым или дифференцируемым по Гато. При этом функционал называют дифференциалом Гато или слабым дифференциалом.
Определение 5.
Пусть приращение функционала
,
заданного в ЛНМП
,
при переходе от точки
в точку
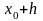 можно представить в виде
можно представить в виде
 ,
,
где
 – линейный и непрерывный по
функционал, а
– линейный и непрерывный по
функционал, а
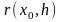 – функционал, удовлетворяющий равенству
– функционал, удовлетворяющий равенству
 .
.
Тогда говорят, что в точке функционал является сильно дифференцируемым или дифференцируемым по Фреше. При этом функционал называют дифференциалом Фреше или сильным дифференциалом.
При этом если функционал является сильно дифференцируемым, то дифференциал Фреше определён однозначно.

