
- •4 Понятие функционала. Функционалы в метрических и линейных пространствах
- •5Формализованные задачи вариационного исчисления. Пространство : норма, метрика, близость элементов. Классификация экстремумов.
- •6. Элементы дифференциального исчисления в л н п: производная по направлению, первая вариация функционала
- •7. Элементы дифференциального исчисления в л н п:дифференцируемость по Гато и Фреше. Дифференциал Фреше линейного непр функционала
- •8 Сильна дифференцируемость функционала
- •9 Условие локального экстремума функционалов
- •10. Простейшая основная задача вариационного исчисления. Необходимое условие экстремума.
- •11 . Основные леммы классического вариационного исчисления (Лагранжа, Дюбуа-Реймона).
- •12 . Уравнение Эйлера (в двух формах).
- •13 Экстремали в регулярном и сингулярном случаях. Теорема Гильберта
- •Экстремали в регулярном и в сингулярном случае
- •14. Случаи упрощения уравнений Эйлера. Примеры
- •15. Простейшая вариационная задача с подвижными границами. Выражение для дифференциала по параметру.
- •16. Простейшая задача с подвижными границами. Необходимые условия экстремума для случая свободных границ и условия трансверсальности
- •17. Экстремали с изломами. Условия Вейерштрасса - Эрдмана.
- •18. Простейшие задачи с ограничениями. Условия в точках сопряжения экстремалей и границ.
- •19. Вторая вариация функционала. Необходимое условие Лежандра.
- •20. Достаточные условия слабого относительного экстремума.
- •3 Примеры содержательных задач о поиске экстремума интегрального функционала
4 Понятие функционала. Функционалы в метрических и линейных пространствах
ПРОСТРАНСТВОМ принято называть множество элементов произвольной природы, в котором тем или иным способом введено понятие предела последовательности его элементов.
МЕТРИЧЕСКИМ
ПРОСТРАНСТВОМ называется множество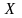 элементов
элементов
 произвольной природы, если каждой паре
его элементов
произвольной природы, если каждой паре
его элементов
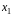 и
и
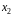 поставлено в соответствие неотрицательное
вещественное число
поставлено в соответствие неотрицательное
вещественное число
 ,
удовлетворяющее трем условиям:
,
удовлетворяющее трем условиям:
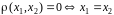 (аксиома тождества).
(аксиома тождества). (аксиома симметрии).
(аксиома симметрии).
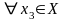 (неравенство треугольника).
(неравенство треугольника).
При этом
число
называют метрическим расстоянием
(или просто расстоянием) от
элемента
до элемента
 ,
а элементы пространства
,
а элементы пространства
 – точками. Перечисленные в
определении условия принято называть
аксиомами метрики.
– точками. Перечисленные в
определении условия принято называть
аксиомами метрики.
ЛИНЕЙНЫМ ПРОСТРАНСТВОМ (над полем вещественных чисел) называется множество элементов произвольной природы, если выполнены следующие условия:
задано правило, в соответствии с которым любым двум элементам
 поставлен в соответствие третий элемент
поставлен в соответствие третий элемент
 ,
который обозначают
,
который обозначают
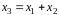 и называют суммой;
и называют суммой;задано правило, в соответствии с которым любому элементу
 и
любому действительному числу
и
любому действительному числу
 поставлен в соответствие элемент
поставлен в соответствие элемент
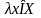 ,
именуемый произведением на
действительное число;
,
именуемый произведением на
действительное число;выполняется свойство коммутативности
 для любых
;
для любых
;операция суммирования обладает ассоциативным свойством
 ;
;
существует нулевой элемент
 такой, что для любого
такой, что для любого
 справедливо равенство
справедливо равенство
 ;
;существует противоположный элемент
 такой, что для любого
справедливо равенство
такой, что для любого
справедливо равенство
 ;
;имеют место ассоциативное свойство
 для любых
для любых
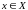 и
и
 ,
а также дистрибутивное свойство
,
а также дистрибутивное свойство
 и
и
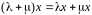 ;
;выполняется условие
 для любого
.
для любого
.
Определение : переменная величина v называется функционалом, зависящим от функции x(t). Что обозначается так: v = v[x(t)], если каждой функции x(t) из некоторого класса функций соответствует значение v, т.е. имеет место соответствие: функции x(t) соответствует число v. (пример – длина дуги криво, соединяющей две заданные точки – м/б вычислено если задано уравнение кривой)
Функциона́л — числовая функция, заданная на векторном пространстве. Функционал берёт в качестве аргумента элемент линейного пространства (вектор) и возвращает в качестве результата скаляр. Довольно часто в роли линейного пространства выступает то или иное пространство функций (непрерывные функции на отрезке, интегрируемые функции на плоскости т. д. Поэтому, неформально говоря, функционал — это функция от функций, переводящая функцию в число (действительное или комплексное).
Примеры
норма функции
неотрицательное число
 – норма элемента, удовлетворяющее
следующим условиям (аксиомам нормы):
– норма элемента, удовлетворяющее
следующим условиям (аксиомам нормы):
 .
. для любого
.
для любого
.
3. 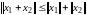 для любых
для любых

значение функции в фиксированной точке
максимум или минимум функции на отрезке
величина интеграла от функции
Пожалуй, самый простой функционал — проекция (сопоставление вектору одной из его координат).
Для следующих трёх
определений будем считать, что область
определения
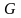 функционала
функционала
 является линейным пространством.
является линейным пространством.
Определение 4. Функционал
называется
однородным функционалом, если
для любого действительного числа
и для любого элемента
 выполняется равенство:
выполняется равенство:
 .
.
Определение 5. Функционал
называется
аддитивным функционалом, если
для любых двух элементов
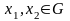 справедливо
справедливо
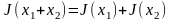 .
.
Определение 6. Функционал называется линейным функционалом, если он одновременно однородный и аддитивный.
Определение 7. Пусть
в метрическом пространстве
с метрикой
задан функционал
.
Этот функционал называют непрерывным
в точке
 ,
если для любого числа
,
если для любого числа
 можно указать такое число
можно указать такое число
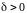 ,
что для всех элементов
,
что для всех элементов
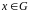 ,
которые удовлетворяют неравенству
,
которые удовлетворяют неравенству
 ,
будет справедливо неравенство
,
будет справедливо неравенство
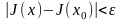 .
.
Если функционал непрерывен в любой точке , то он называется непрерывным в пространстве .
